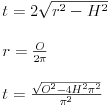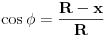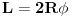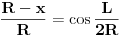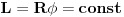[ rade.zrnic @ 06.12.2011. 18:24 ] @
|
| Napravio sam mašinu za izradu oluka (pardon, samo pogon tj. vođenje lima i savijanje tzv. vulcni, to su oni mali savijeni kružići na obodu). Pre nego što bih počeo izradu kotrljajućih kalupa za "prisiljavanje" lima u oblik koji mi treba hteo bih da nacrtam oluk u 3D. Pošto oluk nastaje iz ravnog lima širine 333 mm (trećina širine table) umanjen za širinu dve "vulcne", 20 mm treba da na određeno razmaku postavim više kotrljajućih kalupa za formatiranje luka.
Nije mi problem da to sve i nacrtam ali mi je problem kako da odredim ili izračunam tetive na osnovu dužine poznatog luka (313 mm) na udaljenosti od recimo, dva metra, (tj. u bilo kojoj tački te dužine)? Sužavanje kružnice je linearno.
Pozdrav. |
[ SrdjanR271 @ 06.12.2011. 18:35 ] @
Možeš li da to skiciraš nekako pa cu ti ja izracunati?
[ rade.zrnic @ 06.12.2011. 23:58 ] @
Mogu skicirati, kako da ne, evo tu su slike nekog mog rada. To je ustvari slivna cev ali je u principu isto. Počinje sa ravnim limom a na kraju završava kao zatvorena kružnica. Širina lima bez savijenih krajeva je 313 mm.
Dodatak: svaki od nacrtanih segmenata je udaljen 100 mm
 [Ovu poruku je menjao rade.zrnic dana 07.12.2011. u 01:12 GMT+1]
[Ovu poruku je menjao rade.zrnic dana 07.12.2011. u 01:12 GMT+1][ SrdjanR271 @ 07.12.2011. 14:03 ] @
Nacrtaj tu tetivu.
[ rade.zrnic @ 07.12.2011. 17:44 ] @
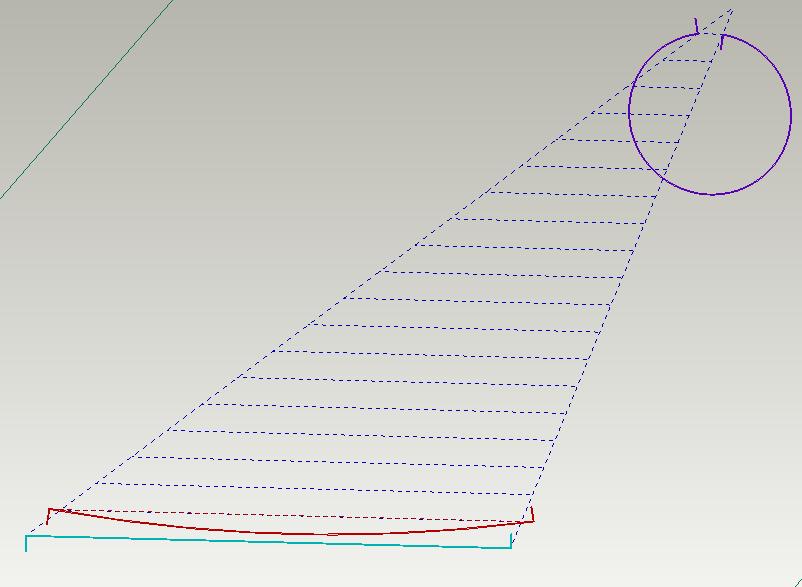
Pa evo tih tetiva, ne poklapaju mi se sa crtežom lukova koji su svi istih cimenzija tj. 313 mm ali su poluprečnici različiti. Poluprečnici ili prečnici kružnica koji se smanjuju do pune kružnice.
 [ zzzz @ 07.12.2011. 18:25 ] @
Ovdje fali funkcija radijusa o položaju.Bez poznavanja radijusa ne možeš računati tetivu ako znaš samo dužinu luka.
Ako na kraju imaš potpuno zatvoren krug onda je tu 2R20=313/pi=99.6 mm
Na početku je R1= beskonačno
Šta sad?Da pretpostavim R2=1000 mm pa linearno interpoliram sve ostale do R20=49.8 mm?
(1000-49.8)/18=52.8 mm.
Imao bi nešto ovako:1000;947.2;894.4:................;102.2;49.8
Meni to ne izgleda dobro.Čini mi se da bi trebali ići na kriterij jednolikog deformiranja,pa bi više ličilo na geometrijski red.Za q=1.81 bilo bi ovako:
1000;846;716;..............;58.8;49.8
Ako znaš kako to treba da bude onda računaj dužinu tangente ovako:
1)izračunaš ugao kojem znaš dužinu luka(313) i R: Fi=313/R (Radijana)
2)Računaš tangentu ovako t=2*R*sin(Fi/2)
Naprimjer za R=846 bilo bi Fi3=313/846=0.37 rad.
t3=2*846*sin(0.37/2)=1692*sin(0.185)=311.2 mm.
[ SrdjanR271 @ 07.12.2011. 19:07 ] @
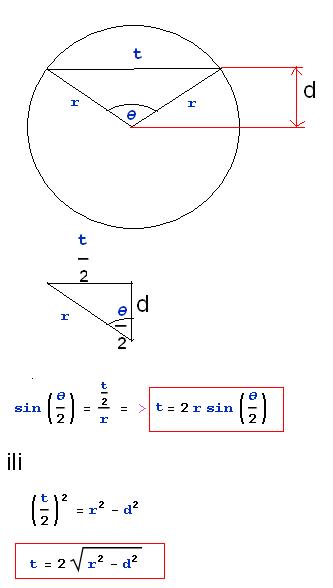
Evo ti ove dve formule, ti vidi možeš li da izmeriš nešto od onih mera.
 [ igorpet @ 07.12.2011. 19:10 ] @
Ako sam dobro razumeo:
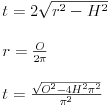
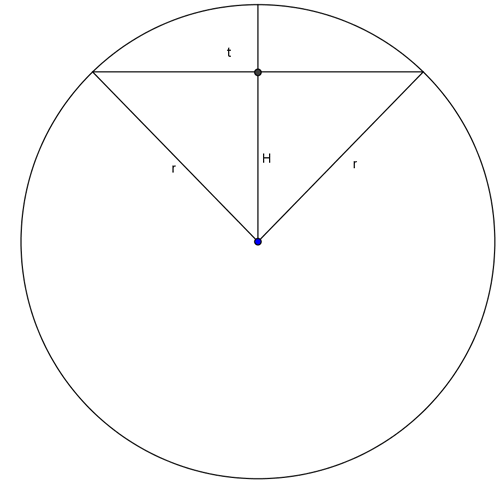
Istovremeno kao prethodna poruka, skoro ... [ darkosos @ 08.12.2011. 10:25 ] @
Citat: kako da odredim ili izračunam tetive na osnovu dužine poznatog luka (313 mm) na udaljenosti od recimo, dva metra, (tj. u bilo kojoj tački te dužine)
U kakvom je odnosu "udaljenosti" sa krugom? Npr da li ima veze sa poluprecnikom itsl?
U stvari, kad malo bolje pogledam, izgleda da te tetive nemaju veze sa kruznicom :) Na onoj slici jednom poruci pre, kao imas samo trougao koji se polako smanjuje...
Da li to znaci da ti samo treba duzina tih paralelnih stranica, koje postepeno zapravo smanjuju krug?
[Ovu poruku je menjao darkosos dana 08.12.2011. u 16:00 GMT+1][ rade.zrnic @ 08.12.2011. 21:15 ] @
U idealnom slučaju bi bilo kao na crtežu "tetive.jpg" tu gore prikazanom, samo što se lim ne ponaša po tom principu, nedozvoljava "stomak" ispod. Pri savijanju krajevi se ponašaju po principu evolvente u prostoru. Mogu lako da odredim tetive po toj skici jer su linearno postavljene. Razmak je 100 mm između svake sledeće skice u ravni u kojoj je tetiva. Ali, uvek ali, ako je sredina dužine luka od 313 milimetara na svakoj skici postavljena na upravnu ravan linijski, onda nemogu odrediti (poluprečnik, prečnik) kružnice u kojoj su dodirne tačke poznatog luka i nepoznate tetive Čini mi se da imam jednačinu sa dve nepoznate...
[ darkosos @ 09.12.2011. 12:57 ] @
Moram priznati da i dalje ne razumem postavku... Izgleda kao da ti rastojanje 100mm iz nekog razloga ne odgovara, ali mi nije jasno zasto.
Sta znaci "ne dozvoljava stomak ispod"? U stvari, najbolje bi bilo kad bi mogao da opises kako ti prelazis iz savijenosti1 u savijenost2?
Duzina luka je ocigledno konstantna tokom celog porcesa, ali nesto tu fali...
[ rade.zrnic @ 10.12.2011. 06:52 ] @
Rastojanje od 100 milimetara mi odgovara jer trebam napraviti obrtne alate na svakoj od tih pozicija, znači ukupno 20 alata ali svaki od njih ima drukčiji radijus pošto se lim mota u kružnicu. Dole je slika sa pogledom od ravnog dela lima pa do zatvorene kružnice. Ako bih skice spustio po slici 2.jpg koja je gore u prethodnom postu, tako da su tačke na kojima je lim savijen pod 90 stepeni u istoj ravni, onda bih dobio ispupčenje, tj. sredina lima bi imala stomak prema dole. Dužina luka tj. širina oluka je konstantno 313 mm i ona je deo kružnice otsečena tetivom koju nemogu da odredim jer mi je nepoznat i dijametar kružnice i tetiva koja otseca poznatu dužinu luka od 313 mm na svakoj skici udaljenoj za po 100 mm.
Poznata mi je ravna širina lima, i zatvorena kružnica udaljena 2000 mm čiji je obim 313 mm i njen prečnik od 99.63 mm.
Taj crtež sam uradio pre nekih dve godine i nesećam se tačno kojom metodom, činimi se da sam radio razlomcima i procentima, početna skica je nula,sledeća udaljena 100 mm je 5 procenata a krajnja 100 procenata. Samo nisam siguran dali je to bilo ispravno.
[ darkosos @ 10.12.2011. 16:02 ] @
Hajde da postavim onda zadatak, pa ti vidi da li ti se uklapa:
Na osnovu luka poznate duzine, oznacimo ga sa L i dela poluprecnika, od centra tetive do kruga,
oznacimo to sa x, treba izracunati poluprecnik R (ili ekvivalentnu, tetivu).
Da bi napravili odnos datih velicina, dodacu jos da je  pola ugla nad tetivom.
Ako je tako, naisao sam na problem:
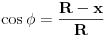 a 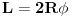 pa se dobija da je 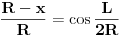 .
Ovo nije bas veselo jer se R odavde ne moze dobiti standardnim putem... Znaci ili neki drugi pristup ili neka aproksimacija... [ rade.zrnic @ 10.12.2011. 17:29 ] @
Našao sam radove od pre par godina kad sam počeo da radim spravu. Neznam dali ću uspeti da to postavim tj. prikačim ali ću pokušati, ako ne uspem poslaću na PP.Radovi su u Excel-u. valjda ćeš uspeti da se snađeš...
[ rade.zrnic @ 10.12.2011. 17:37 ] @
Nisam matematičar, valjda me možeš razumeti, borim se, eto tu su primeri... Da bih završio spravu nemogu da lutam probajući dali je radius alata odgovarajući , pa se obraćm onima koji sigurno znaju više od mene.
[ rade.zrnic @ 10.12.2011. 18:09 ] @
Zaboravio sam na neke smernice u fajlu "Izračunavanje ugla oluka"; polja sa dodatim komentarom su za izmenu i utiču na sve rezultate u poljima koji su zavisni, možda jemalo konfuzno ali tako sam radio...
[ zzzz @ 11.12.2011. 11:07 ] @
Ako praviš mašinu,neke valjke ili tako nešto, koj će u 19 koraka ravnu traku iz bunta smotati u cijev željene dužine,onda je najbolje primjeniti princip ravnomjerne deformacije.
Ukupna deformacija vanjskog (ali i unutrašnjeg) sloja lima u odnosu na središnji sloj je dL=s*pi (debljina lima s puta 3.14).Podijeli to na 19 dijelova.Sad kada znamo dužinu vanjskog luka i dužinu unutrašnjeg luka,možemo izračunati radijus i ugao fi.
r*fi=313-*s*pi/19
(r+s)*fi=313+*s*pi/19
Iz poznatih r i ugla računaš dužinu tangente t=2r*sin(fi/2).
[ darkosos @ 12.12.2011. 07:51 ] @
Da, princip ravnomerne deformacije definitivno zvuci dobro, mada nisam bas najbolje razumeo :)
Sa matematicke tacke gledista me kopka sta je ona kriva koja se dobija kada se spoje vrhovi lima pri savijanju...
[ rade.zrnic @ 12.12.2011. 11:02 ] @
darkoss:
"Sa matematicke tacke gledista me kopka sta je ona kriva koja se dobija kada se spoje vrhovi lima pri savijanju."
Pa to je upravo ono što i mene kopka...
Ako crtam po formuli koju sam predstavio sa "postupak procenta" u "izračunavanje ugla oluka.xls" i postavim sredine skica u istoj ravni, dobijam tu krivu, ali ako tu krivu pokušam da predstavim linearno tj. pokušam da spustim skice koje će u upravnoj ravni biti poravnate po temenima, dobijam "stomak" po sredini skica prema dole. Prosto, nisam siguran dali je način na koji sam izračunavao poluprečnike i tetive ispravan.Liči mi na nešto kako bi trebalo da izgleda, ali ne dobacujem dotle...
[ rade.zrnic @ 12.12.2011. 11:13 ] @
Sad se opet setih... Neide ravnomerna deformacija. Ukoliko bi bila ravnomerna deformacija linearno, negde mora da bude "stomak, ili bi dobili elipsu ili bi se lim negde gužvao. Mora da bude kriva kao što je na crtežu ali nisam siguran dali sam dobro izračunavao tj. dali je moja koncepcija ispravna?
[ darkosos @ 12.12.2011. 12:46 ] @
Pa sad ne znam na kakvu je ravnomernu deformaciju mislio Milan, ali meni izgleda, na tom crtezu gde je fiksiran "stomak" svih polozaja,
da je rastojanje krajeva lima podjednako... To mi izgleda ok, ali jos ne znam kako se to matematicki dobija...
Da, svakako da se ne misli na linearnu ravnomernu deformaciju, vec na kolicinu zakrivljenosti dve uzastopne krive u tom nizu.
Dodacu ovde: posto je 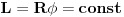 onda ako podelis ugao fi, koji ide od 0 do 2pi, dobijas R a samim tim i ostalo sto ti treba.
[Ovu poruku je menjao darkosos dana 12.12.2011. u 14:07 GMT+1]
[Ovu poruku je menjao darkosos dana 12.12.2011. u 14:16 GMT+1][ zzzz @ 12.12.2011. 16:00 ] @
Ravnomjernost deformacije:
Ravni lim motamo u cijev.Dobijemo šuplji valjak.Vanjski radijus valjka je veći od unutrašnjeg za debljinu lima s.Vanjski obim je veći od unutrašnjeg.Lim širine 313 mm se na vanjskoj plohi nešto istegao,a na unutarnjoj plohi sabio.Ukupna deformacija je poznata (s*3.14).
Neka se ta ukupna deformacija odvija postepeno i jednako na svakom koraku,a ima ih 19.
Trbusi i elipse:
Sredina trake 156.5+156.5 mora uvjek ležati (prisilno) na pravcu koji u produžetku leži na izvodnici cijevi oluka.
koordinate rubova lima:
Ovo jeste neka krivulja slična zavojnici.Ako znamo R i fi za svih 20 položaja možemo uzeti gore spomenutu izvodnicu kao jednu osu.Na njoj imamo tačke od 0 do 2000mm na svakih 100 mm.
Druge dvije koordinate izračunamo iz R i fi.
x=R sin(fi/2), y=R (1-cos(fi/2),Ovakav tablični prikaz krivulje je dovoljan za konstrukciju dijelova mašine.
Meni je nejasno kojom tehnologijom će se deformacija izvoditi.
-Da li je to sistem valjaka kao kod izrade šavnih cijevi ili krovnih panela?
(skica)
-Da li je to povlačenje sa prisilnim vođenjem rubova po gore spomenutim krivuljama?
-Možda neka kombihacija ovoga ili nešto treće?
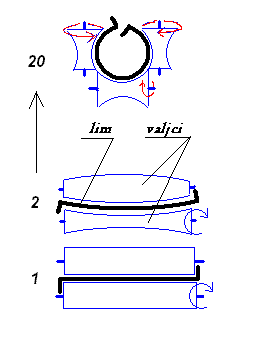
[ rade.zrnic @ 12.12.2011. 17:53 ] @
Evo Darko, ja sam pojednostavio ono što sam radio, a kako sam došao do toga nemam pojma... Kad unesem procenat vrednosti udaljenosti do 2000 mm dobijam neke suvisle rezultate koji odgovaraju onome što sam crtao.Radim u PtcProDesktop-u koji je stariji brat (davno zaboravljen) PtcProEnginer-a. Ponaša se dobro. E sad, možeš li analizirati ili izvući neku formulu iz tog postupka u Excel-u?
[ rade.zrnic @ 12.12.2011. 17:55 ] @
Izvini Milane, nisam video da si i ti komentarisao, obraćam se i tebi kao i Darku...
Upravo tako kako si i predpostavio u prvom pitanju, savijane valjcima
[ darkosos @ 12.12.2011. 18:00 ] @
Meni se cini da Milan zna sta prica, pa vidi da li ti odgovara njegov pristup. Ja cu se zadovoljiti ako nadjem jednacinu te krive :)
[ dusans @ 12.12.2011. 20:55 ] @
Evo ja sam ti napravio Excel gde možeš da vidiš proračun dužine tetiva.
Primer koji sam postavio pravi eksponencijalni rast poluprečnika kružnice na kojoj leži luk.
Rast poluprečnika je u 20 koraka - od 49,81 mm pa do 747,23 mm (15*49,81).
Predlažem ti da staviš neki svoj metod rasta poluprečnika (kolona r) sa rastom udaljenosti od početka ako ti se priloženi ne sviđa, ostatak proračuna ti je već tu.
[ rade.zrnic @ 13.12.2011. 05:49 ] @
Dušane, hvala na trudu, danas ću da uradim crtež tim načinom, rezultat ću da postavim večeras.
Kako si dožao do "Eksponent 1,153186474"
U svakom slučaju, zahvaljujem svima na volji.
[ rade.zrnic @ 13.12.2011. 08:52 ] @
Ipak nisam izdržao do večeras, napravio sam skice. Dušane, sa tim načinom sam se borio i ranije i rezultati su vidljivi u crtežima. Prva skica, počevši od ravnog lima biva podignuta nešto jače ali su sve ostale do pred sami kraj samo blago podizanje da bi u par završnih došlo do oštrog podizanja. Zadnju skicu program odbija da "loftuje" ili izvlači jer je greška u crtežu... Preklapaju se linije tj. Radijus je manji od onog koji daje obim. Urađeno po tvojoj formuli... Nisam namerno redigovao skicu da vidiš kotu kružnice.
Probaj sa onim načinom koji sam upotrebio, postupak procenta, živo me interesuje dali sam ipak pogodio?
Neznam baš puno o matematici, samo kljucam k'o ćorava kokoška.
PS.
Ups, "Radijus je manji od onog koji daje obim.", pogrešno sam se izrazio, radijus je ekvivalent obimu ali mi se preklapaju linije skice i program to vidi kao grešku.
[Ovu poruku je menjao rade.zrnic dana 13.12.2011. u 10:19 GMT+1]
[ darkosos @ 13.12.2011. 10:17 ] @
Evo i mog skromnog doprinosa :)
[ rade.zrnic @ 17.12.2011. 05:49 ] @
Prob'o 'vako prob'o 'nako ali ne dobijam zadovoljavajuće rezultate.
U stvari radijus od +- 0.1 mm mi neznači ništa, kad "ostružem" valjke oni će ionako da budu u toleranciji ali me je zaintrigirao način (geometrijsko-matematički) tačnog izračunavanja. Pitagora umro, što ću sade, koga da pitam?
[ rade.zrnic @ 20.12.2011. 05:28 ] @
Evo jedne adrese gde se vidi kako mašina za izradu oluka "operiše" i to na terenu. Valjci koji oblikuju lim su kritični što se tiče tačnosti.
http://www.youtube.com/watch?v=3EqeWAHVisE[ dusans @ 20.12.2011. 23:04 ] @
Evo novog Excela pa pogledaj.
Mislim da je fora u tome da ne treba razvijati priču po poluprečniku ili prečniku,
već po uglu luka u jednakim koracima, tako je urađeno u ovom primeru.
Takođe sam napravio i proračun za vrednosti na proizvoljnoj udaljenosti.
Pozdrav!
Edit:
Zakacio sam i jedno programče gde mozes da paste-uješ podatke za r i ugao luka iz excela i koje ilustruje rezultat.
Moras da imas instaliran .Net 2.0 da bi ga pokrenuo.
[Ovu poruku je menjao dusans dana 21.12.2011. u 00:20 GMT+1]
[ rade.zrnic @ 21.12.2011. 05:10 ] @
Zahvaljujem na trudu Dušane. Pozdrav
Neće da se pokrene .exe fajl iz .zip foldera, signalizira grešku na jednoj adresi.
[ darkosos @ 21.12.2011. 07:24 ] @
Ono sto sam ja zakacio ovde je takodje po uglu luka...
[ dusans @ 21.12.2011. 08:55 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|