[ atelago @ 08.12.2011. 16:28 ] @
| Pretpostavljam da Bojan Bašić neće odmah da i ovu temu prenese u mad zone, bar ne dok je dobro ne pogleda |
|
[ atelago @ 08.12.2011. 16:28 ] @
[ atelago @ 08.12.2011. 19:17 ] @
Princip je sledeći:
Ako postavimo tri jednake kružnice unutar ugla tako da su im centri jednako udaljeni od vrha zadatog ugla – onda se tangente na te kružnice, koje prolaze tim vrhom seku pod istim uglom za svaku kružnicu – jedini je problem pronaći kontaktni položaj kružnica, međutim, to je moguće učiniti i bez jednakog pomeranja kružnica prema vrhu. Dakle, ako ostvarimo jednaku udaljenost centara kružnica prema vrhu kada su kružnice u kontaktu, pa ako krajnje kružnice tangiraju krakove zadatog ugla i ako su kružnice međusobno jednake, onda tangente na te kružnice koje prolaze vrhom zadatog ugla zatvaraju jednake uglove. Sve ove zahteve moguće je ispuniti. [ Bojan Basic @ 08.12.2011. 20:15 ] @
[ atelago @ 08.12.2011. 20:39 ] @
Možda tako izgleda zbog lošeg crteža, ali to mora biti tangenta jer su te kružnice jednako udaljene od tačke O'
Laptop mi je na izmaku - jedva sam i to poslao. Potrudiću se da dam detaljniju sliku sa sve tri kružnice i sa detaljnim objašnjenjem. Najvažnije je ostvariti kontaktni položaj kružnica. (i sam možeš dopuniti sliku drugom polovinom tako da imaš sve tri kružnice - biće jasnije) Na početku je već rečeno da su centri tih kružnica jednako udaljeni od tačke O, a oko tačke O' sve je isto samo umanjeno - dakle zadržana je sličnost odnosno jednakost sa uglom AOB i t. d. [ Bojan Basic @ 08.12.2011. 21:48 ] @
[ SrdjanR271 @ 08.12.2011. 22:16 ] @
Ako sam dobro razumeo atelagovu konstrukciju, evo šta dobijam za ugao od 45 stepeni:
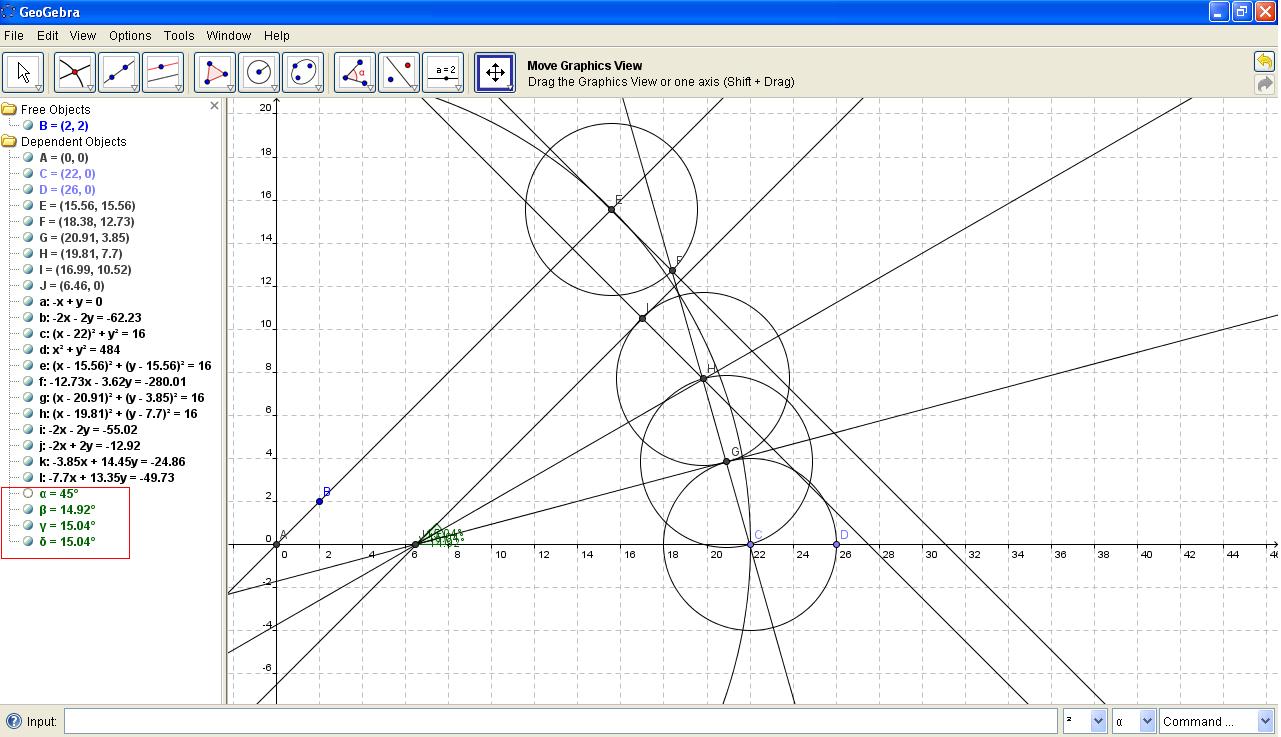 [EDIT] Evo za ugao od 75.96 stepeni. 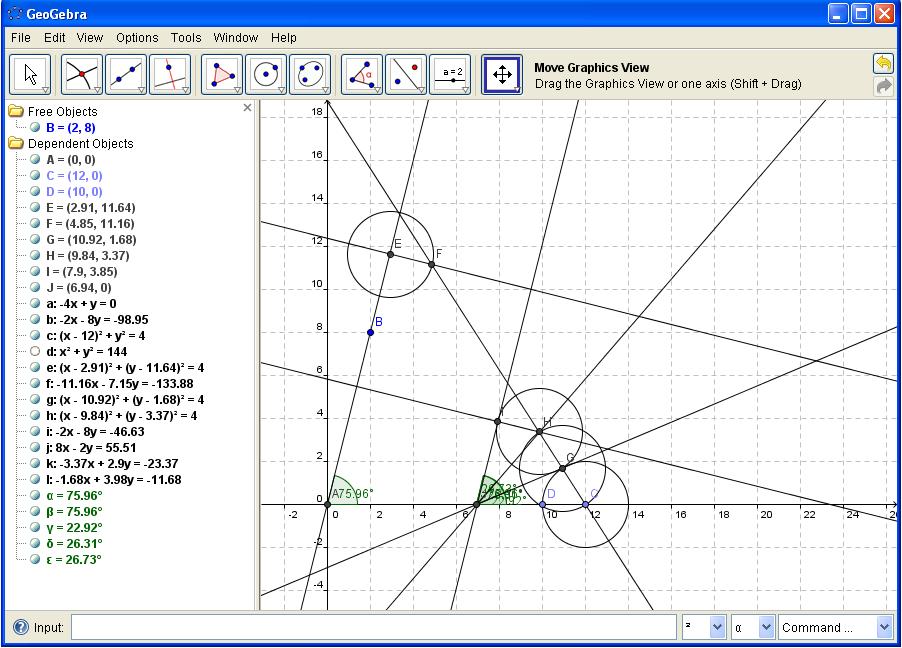 [Ovu poruku je menjao SrdjanR271 dana 08.12.2011. u 23:36 GMT+1] [ atelago @ 08.12.2011. 23:11 ] @
Ako tri tačke približavaš četvrtoj tako da su od nje uvek jednako udaljene onda te tri tačke uvek čine slične trouglove odnosno zadržavaju međusobne odnose. Ako te to buni što sam ja uradio ne približavajući se vrhu ugla, učini to ti na taj način i dobićeš identičnu sliku. [ atelago @ 08.12.2011. 23:14 ] @
Ako tri tačke približavaš četvrtoj tako da su od nje uvek jednako udaljene onda te tri tačke uvek čine slične trouglove
odnosno zadržavaju međusobne odnose. Ako te to buni što sam ja uradio ne približavajući se vrhu ugla, učini to ti na taj način i dobićeš identičnu sliku. [ SrdjanR271 @ 08.12.2011. 23:22 ] @
Aj ti to napravi u flash-u ili snimi pa na YT.
Da ne nagađam ovako. [ atelago @ 09.12.2011. 05:42 ] @
Pogledaj ovaj crtež:
[ Nedeljko @ 09.12.2011. 09:06 ] @
Svojevremeno je Bojan Bašić napisao da smatra da je član atelago zapravo galet@world, tj. da korisničko ime "atelago" zapravo znači "osveta galeta" (treba čitati unazad). Mada je to bilo jasno i iz stavova koje član atelago zastupa, on je negirao da je on zapravo banovani član galet@world. No, sada imamo i dokaz "crno na belo" da se radi o istoj osobi. Fajl priložen u prvoj poruci sa ove teme je potpisan sa "Dane Gaćeša", što je pravo ime člana galet@world.
[ SrdjanR271 @ 09.12.2011. 10:00 ] @
Joj bravo Nedeljko.
Nisam skrolovao do dna, ladno se potpisao. Znao sam ja da je to on. [ Bojan Basic @ 09.12.2011. 10:27 ] @
Citat: atelago: ...čine slične trouglove odnosno zadržavaju međusobne odnose. Postupak iz prve poruke ne daje nikakve slične trouglove iz kojih bi sledio zaključak koji navodiš. Ako tvrdiš suprotno, napiši koji tačno trougao iz prve poruke je sličan s kojim, zašto su slični (navedi koji stav o sličnosti primenjuješ), i kako iz te navodne sličnosti sledi podudarnost onih duži koje tebi trebaju. Ukoliko to odbiješ da učiniš ili opet počneš s nekim nepovezanim analogijama, zaključiću da se i dalje ponašaš u skladu sa starom praksom pa pokrenuti postupak za tvoje ponovno udaljavanje s foruma. [ Nedeljko @ 09.12.2011. 12:10 ] @
Ja mislim da bi trebalo da se uvede pravilo da ko god hoće da kači trisektore i slične nemoguće stvari prvo mora da okači geogebra fajl sa svojom konstrukcijom, jer se inače ne vredi raspravljati.
[ atelago @ 09.12.2011. 13:44 ] @
Citat: Nedeljko: ... on je negirao da je on zapravo banovani član galet@world. U kojoj poruci sam to učinio? Citat: Bojan Basic: Postupak iz prve poruke ne daje nikakve slične trouglove iz kojih bi sledio zaključak koji navodiš. Ako tvrdiš suprotno, napiši koji tačno trougao iz prve poruke je sličan s kojim, zašto su slični (navedi koji stav o sličnosti primenjuješ), i kako iz te navodne sličnosti sledi podudarnost onih duži koje tebi trebaju. Ukoliko to odbiješ da učiniš ili opet počneš s nekim nepovezanim analogijama, zaključiću da se i dalje ponašaš u skladu sa starom praksom pa pokrenuti postupak za tvoje ponovno udaljavanje s foruma. Vrlo rado ću učiniti to šta tražiš. Ako produžimo duž c1c2 tako da seče krak OA u tački koju možemo označiti sa s2 i ako već postojeći presek te duži sa krakom O'A' označimo sa s2' onda imamo dva slična truogla - veliki O,s2,c1 i mali O',s2 'c1. Oni su slični po jednakosti uglova. Mali trougao je nacrtan zato što u velikom trouglu ne mogu da izvršim podelu ugla AOB a u malom mogu, što sam i učinio. Podudarnost elemenata u malom truoglu ne sledi iz sličnosti već iz činjenice da je tačka O' jednako udaljena od centara kružnica c1 i c2' Elementi i to O'c2' i tangenta između kružnica c1 i c2' odnosno njihovi smerovi zbog sličnosti trouglova važe i za veliki trougao jer je i sam zadatak postavljen tako da se izvrši trisekcija ugla AOB koji pripada velikom trouglu. Sve ovo se mnogo jasnije vidi na mom grafičkom prilogu "kontaktne tačke". Iz tog priloga se vrlo jasno vidi i sledeće 1. Tri jednake kružnice su u međusobnom kontaktu i u kontaktu sa krakovima zadatog ugla 2. Udaljenost centara tih kružnica od vrha ugla je jednaka Ovo su potrebni i dovoljni uslovi da se taj ugao podeli na tri jednaka dela. Ako to nije tako ja molim nekoga ko vidi gde je tu greška da je saopšti jer zaista to je u ovom trenutku najvažnije. Ja sam imao ovo rešenje i registrovao ga i pre onog dana kada sam poslao moj post "Mehanička trisekcija", ali se nisam usuđivao da ga prikažem ovde dok ga dobro ne proverim. Stoga ću biti veoma zahvalan onom ko vidi i saopšti mi ono šta ja ne vidim. [ SrdjanR271 @ 09.12.2011. 13:59 ] @
Možda ovde http://www.elitesecurity.org/p2909368.
Citat: Zašto bih ja osvećivao galeta? Da li sam mojim porukama nekom naneo zlo koje liči na osvetu? Nekada sam živeo u Babinu Potoku pored Plitvica. Otuda i potiče "ate lago". Pošto sam poistovećen sa galetom neko vreme nisam imao pristup ovde, pa nisam mogao da odgovorim, slučajno sam otkrio da mogu da se ulogujem i to sada koristim ukoliko me sličnost sa galetom ne diskvalifikuje. [ Bojan Basic @ 09.12.2011. 14:24 ] @
Citat: atelago: Podudarnost elemenata u malom truoglu ne sledi iz sličnosti već iz činjenice da je tačka O' jednako udaljena od centara kružnica c1 i c2' Nije tačno. Slažem se da su ovi trouglovi koje si opisivao u prethodnoj poruci slični. Takođe se slažem da u „velikom“ trouglu važi 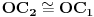 (takav je bio zahtev prilikom konstrukcije). Ali iz ove podudarnosti i sličnosti „velikog“ i „malog“ trougla prosto ne sledi da je u „malom“ trouglu duž (takav je bio zahtev prilikom konstrukcije). Ali iz ove podudarnosti i sličnosti „velikog“ i „malog“ trougla prosto ne sledi da je u „malom“ trouglu duž 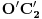 podudarna s onom drugom isprekidanom duži. podudarna s onom drugom isprekidanom duži.Ostatak tvojih crteža („kontaktne tačke“ i varijacije na temu) nije sporan. Jasno je na kakvu konfiguraciju pokušavaš da svedeš konstrukciju, i jasno je da bi, kad bi to uspeo, ugao stvarno bio podeljen na tri podudarna dela. Problem je samo što ti takvu konfiguraciju ne dobijaš svojim metodom. Citat: Nedeljko: Ja mislim da bi trebalo da se uvede pravilo da ko god hoće da kači trisektore i slične nemoguće stvari prvo mora da okači geogebra fajl sa svojom konstrukcijom, jer se inače ne vredi raspravljati. Teško bi i to pomoglo. Evo, Srđana nije mrzelo da izvrši konstrukciju u GeoGebri, pa se ispostavilo da delovi na koje je polazni ugao podeljen stvarno nisu podudarni (što je, naravno, bilo jasno od početka), ali i da je razlika među njima praktično nevidljiva golim okom. Ne verujem da bi to pokolebalo nekoga ko je ubeđen u ispravnost svoje konstrukcije. [ atelago @ 09.12.2011. 17:04 ] @
Citat: [url=/p3007596]Ali iz ove podudarnosti i sličnosti „velikog“ i „malog“ trougla prosto ne sledi da je u „malom“ trouglu duž podudarna s onom drugom isprekidanom duži. Molim te, pokaži mi gde sam to rekao. Podudarne su duži (t.j. imaju iste dužine) O't' i isprekidana duž od O' pa do kontakta kružnica jer su to tangente na kružnicu k2' i prolaze kroz O'. Duž O'c2' je simetrala ugla koji zatvaraju te dve tangente jer prolazi centrom c2' Izvinjavam se ako sam na bilo koji način doveo ove stvari u pitanje. Citat: Problem je samo što ti takvu konfiguraciju ne dobijaš svojim metodom. Da ponovim moj metod. Govoriću o metodu prikazanom u grafičkom prilogu "kontaktne tačke" Nacrtaću "veću" kružnicu sa centrom u vrhu zadatog ugla. Tamo gde ta kružnica preseca krakove ugla biće kontaktne tačke kružnica i krakova ugla. Centri tih kružnica biće na "većoj" kružnici t.j. te kružnice biće jednako udaljene od vrha ugla. Na preseku simetrale ugla i "veće" kružnice biće centar srednje kružnice. Dakle, sve tri kružnice su jednako udaljene od vrha ugla. Neka kružnice nisu u kontaktu već na izvesnom odstojanju koje zavisi i od te "veće" kružnice - zato sam je tako i nazvao. Neka se kružnice približavaju vrhu ugla, ali uvek tako da im se centri nalaze na nekoj koncentričnoj kružnici sa centrom u vrhu ugla. Približavanje na ovaj način traje sve dok se ne ostvari kontakt između kružnica. Dakle, kružnice su u kontaktu i međusobnom i sa kracima ugla i na jednakom rastojanju od vrha ugla. To je ostvarivo samo uz uslov da je zadati ugao podeljen na tri jednaka dela tangentama koje prolaze vrhom ugla. Naravno, to nije geometrijski pristup, ali on nam nije ni potreban. Nas interesuje kontaktni položaj kružnica koji je definisan kontaktnim tačkama. A kontaktne tačke se tokom približavanja ne menjaju i one se nalaze na preseku kružnica i duži koja spaja njhove centre nezavisno od toga na kojoj koncentričnoj ("većoj") kružnici se nalaze njihovi centri. Gde sam pogrešio? [ SrdjanR271 @ 09.12.2011. 17:15 ] @
Promenio si početni metod, al ajde.
Ja sam te dovde razumeo. Kontam da ako povećamo prečnike kružnice u H i E i dodirnu se u jednoj tački, povučemo polupravu kroz tu tačku i dobijamo četvrtinu ugla? 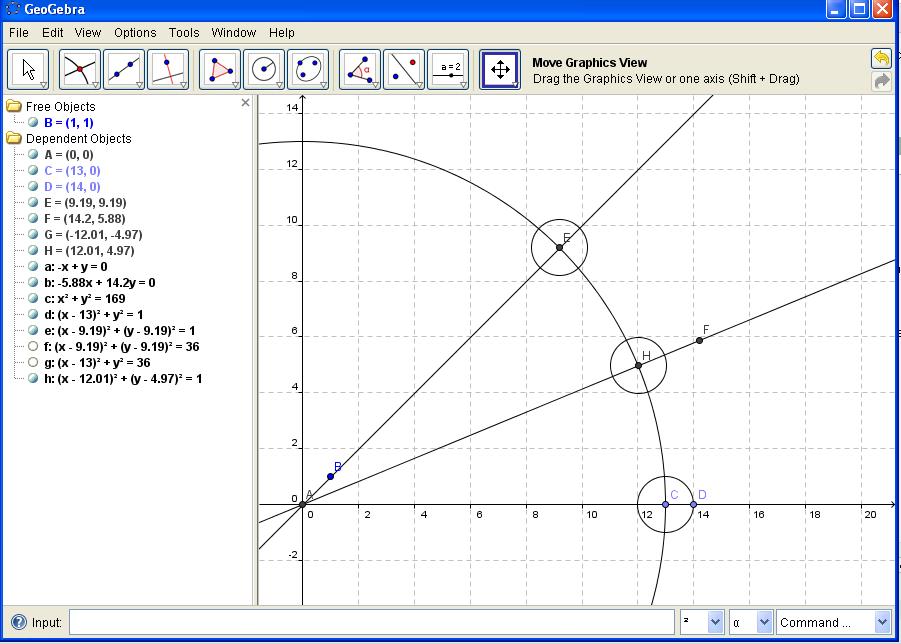 [ Bojan Basic @ 09.12.2011. 19:45 ] @
Citat: atelago: ...mora biti tangenta jer su te kružnice jednako udaljene od tačke O' Citat: atelago: Podudarne su duži (t.j. imaju iste dužine) O't' i isprekidana duž od O' pa do kontakta kružnica jer su to tangente Dakle, odluči već jednom: da li iz jednake udaljenosti sledi da su to tangente, ili iz toga da su tangente sledi jednaka udaljenost? Možeš se ti do sutra vrteti ukrug s ovim tvrdnjama (da druga sledi iz prve, a prva sledi iz druge), ali ni jedna ni druga ne važi u tvojoj konstrukciji iz prve poruke. Ako tvrdiš drugačije, izvoli dokaži da u tvojoj konstrukciji važi bilo koja od ove dve tvrdnje. Prvo sam shvatio da tvrdiš kako to sledi zbog sličnosti — u poslednjoj poruci kažeš da nije zbog sličnosti; dobro, ali onda kaži zbog čega jeste (samo ne tako što ćeš reći da jedna tvrdnja sledi iz druge, a druga iz prve). Naglašavam da to dokažeš u tvojoj konstrukciji, jer vidim da u poslednjoj poruci opet pričaš o „kontaktnim tačkama“ — ono što pričaš o toj konfiguraciji jeste tačno, i ne moraš više ponavljati tu priču po  -ti put, nego izvoli dokaži da u prvoj poruci važi ovo što je sporno. Dok to ne dokažeš, ti u svojoj konstrukciji nemaš konfiguraciju s „kontaktnim tačkama“, pa džabe razglabaš o njoj. -ti put, nego izvoli dokaži da u prvoj poruci važi ovo što je sporno. Dok to ne dokažeš, ti u svojoj konstrukciji nemaš konfiguraciju s „kontaktnim tačkama“, pa džabe razglabaš o njoj.[ Nedeljko @ 09.12.2011. 20:09 ] @
atelago
Pusti na trenutak dokaze konstrukcije. Ako geogebra za konstrukciju daje rezultate koji se numerički ne slažu sa tvojom konstrukcijom, onda ti konstrukcija ne valja i ne moraš da se trudiš da je dokazuješ. [ atelago @ 09.12.2011. 23:10 ] @
Citat: Bojan Basic: Dakle, odluči već jednom: da li iz jednake udaljenosti sledi da su to tangente, ili iz toga da su tangente sledi jednaka udaljenost Bojane, ja stalno tvrdim da su centri kružnica jednako udaljeni od vrha ugla. Ili da se centri kružnica nalaze na nekoj od koncentričnih kružnica koje imaju centar u vrhu ugla. Ta je naročito važno, ali se gubi iz vida. Prema tome iz tog uslova sledi ostalo. U konkretnom slučaju mali trougao treba shvatiti kao da smo došli u kontaktni položaj pri vrhu zadatog ugla. Dakle, udaljenosti centara kružnica od tačke O' su jednake po samoj postavci principa rešavanja zadatka. Tangente, naravno, moraju biti jednake jer prolaze kroz tačku O' Mislim, da sam pogrešio utoliko što sam umesto tri kružnice u prvoj poruci prikazao ustvari jednu i po i otuda slede nejasnoće kojih ne bi bilo da sam drukčije uradio. Citat: Dok to ne dokažeš, ti u svojoj konstrukciji nemaš konfiguraciju s „kontaktnim tačkama“, pa džabe razglabaš o njoj. Što se tiče konfiguracije koju pominješ - ona je upravo određena tim uslovom da su centri kružnica jednako udaljeni od vrha ugla. Zašto? Zato što bi položaj kontaktnih tačaka bio drukčiji kad bi centri kružnica bili jednako udaljeni od neke druge tačke a ne vrha ugla. Prema tome kontaktna konfiguracija kružnica zavisi upravo od tog uslova i može biti samo takva. Citat: Nedeljko: atelago Pusti na trenutak dokaze konstrukcije. Ako geogebra za konstrukciju daje rezultate koji se numerički ne slažu sa tvojom konstrukcijom, onda ti konstrukcija ne valja i ne moraš da se trudiš da je dokazuješ. Nedeljko, ja mojom konstrukcijom mogu da podelim ugao na tri dela a da uopšte ne znam koliki je taj ugao niti njegove trećine. Znam samo šta je ceo ugao a šta njegova trećina. Pošalji neki "pristojan" ugao i podeliću ti ga, a ti proveri trećine preklapajući ih pa ih posle saberi. Uvek se lako može neki veliki ugao podeliti na četiri dela, pa onda deliš jedan deo na tri dela i dodaš onim ostalim i t. d. Ima raznih mogućnosti. Čak i neko malo područje uglova koje delimo na tri dela može u celosti da završi posao za sve uglove. [ atelago @ 10.12.2011. 08:12 ] @
Da pojednostavnima problem do maksimuma jer izgleda da je trisekcija vrlo jednostavna
Evo: Stavimo tri jednaka kruga u zadati ugao tako da su im centri jednako udaljeni od vrha i trisekcija je gotova Tangente na te krugove koje prolaze vrhom ugla dele zadati ugao na tri jednaka dela Konfiguracija kontaktnog položaja krugova je određena kontaktnim tačkama koje su definisane upravo tim uslovom t.j. da su krugovi jednako udaljeni od vrha ugla bili oni u kontaktu ili ne. Ili: Konfiguraciju kontaktnog položaja krugova možemo odrediti iz bilo kog položaja krugova koji zadovoljava uslov da su krugovi jednako udaljeni od vrha ugla. [ atelago @ 10.12.2011. 16:15 ] @
Citat: atelago: Konfiguracija kontaktnog položaja krugova je određena kontaktnim tačkama koje su definisane upravo tim uslovom t.j. da su krugovi jednako udaljeni od vrha ugla bili oni u kontaktu ili ne. Ili: Konfiguraciju kontaktnog položaja krugova možemo odrediti iz bilo kog položaja krugova koji zadovoljava uslov da su krugovi jednako udaljeni od vrha ugla. Ovo nije tačno! Ljut sam na sebe. Sad možete i da me banujete. Neka vam je prosto. [ Bojan Basic @ 11.12.2011. 01:27 ] @
Citat: atelago: Bojane, ja stalno tvrdim da su centri kružnica jednako udaljeni od vrha ugla. Ili da se centri kružnica nalaze na nekoj od koncentričnih kružnica koje imaju centar u vrhu ugla. Ta je naročito važno, ali se gubi iz vida. Nisam ništa gubio iz vida — već ti zahtevaš da su centri kružnica jednako udaljeni od vrha polaznog ugla (tj., od tačke  ), no nije tačno da su jednako udaljeni i od tačke ), no nije tačno da su jednako udaljeni i od tačke  . .Ako dobro tumačim tvoju poslednju poruku, i sam si uvideo grešku. U tom slučaju mi je drago što smo razumeli. Nije problem pogrešiti, niko nije bezgrešan, ali je bitno grešku uvideti. [ atelago @ 11.12.2011. 04:16 ] @
Citat: Bojan Basic:Ako dobro tumačim tvoju poslednju poruku, i sam si uvideo grešku. Ako govorimo o približavanju kružnica tački O onda spojnica njihovih centara menja smer jer se samo srednja kružnica približava tački O radijalno, a ostale dve ne. To sam ja izgubio iz vida. Hvala ti na strpljenju. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|