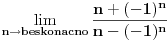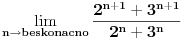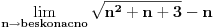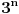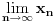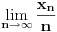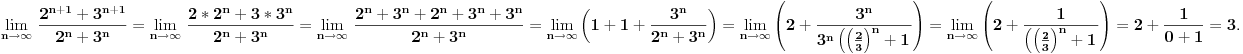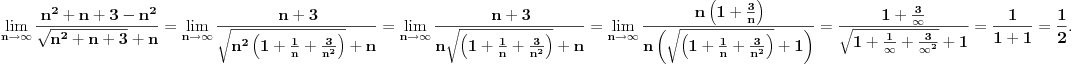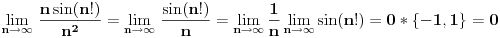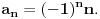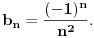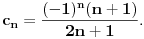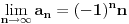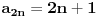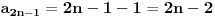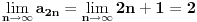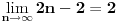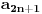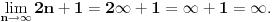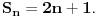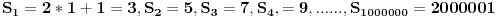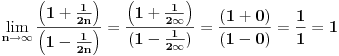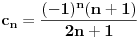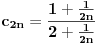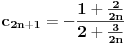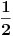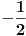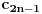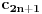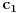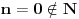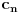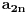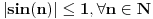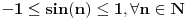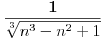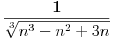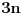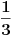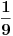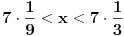[ patkan1992 @ 09.12.2011. 10:07 ] @
|
[ SrdjanR271 @ 09.12.2011. 11:37 ] @
Za niz
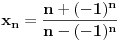 , posmatrajmo sledeća dva podniza: , posmatrajmo sledeća dva podniza: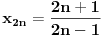 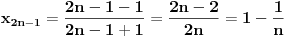 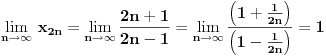 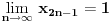 Pošto oba podniza konvergiraju ka broju 1, onda i niz  konvergira ka 1. konvergira ka 1.Ograničen je odozgo sa 3, što se vidi iz 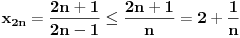 . .Ograničen odozdo sa 0 što se vidi iz 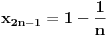 . .Nije monoton, jer "šeta", {0, 3, 0.5, 1.66667, 0.666667, 1.4, 0.75, 1.28571, 0.8, 1.22222, 0.833333, 1.18182, 0.857143, ...}. Evo i grafički : 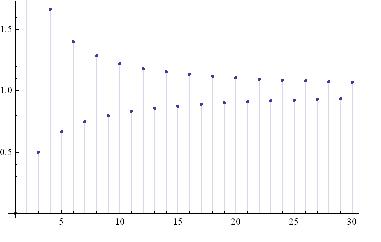 Za ostale probaj sam, pa ako zapneš javi. Najlakše je naći limes. (po meni). [ Sonec @ 09.12.2011. 12:06 ] @
[ SrdjanR271 @ 09.12.2011. 12:11 ] @
[ patkan1992 @ 09.12.2011. 16:21 ] @
Ok, ovo iz poslednjeg posta mi je jasno. Samo jedno: nula niz je
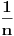 ? ?Sto se tice prvog posta, uokvirio sam: [url]http://i41.tinypic.com/jpenow.png[/url] Prvo uokvireno: Odakle su uopste nastala ova dva podniza? (Ako mozes detaljno da mi objasnis, jer nisam nikako upucen u ovo...) Drugo: Odakle se stvorilo ovo 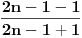 ? ?I trece i cetvrto: Ne kapiram uopste kako se vidi da je ogranicen i zasto je ogranicen... A takodje ne razumem ni kako si dosao do ovih brojeva kod zakljucka da nije monoton? I odakle ovo: 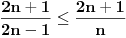 , tacnije ovaj izraz posle znaka , tacnije ovaj izraz posle znaka 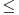 . .[ SrdjanR271 @ 09.12.2011. 16:36 ] @
Citat: patkan1992: Prvo uokvireno: Odakle su uopste nastala ova dva podniza? (Ako mozes detaljno da mi objasnis, jer nisam nikako upucen u ovo...) Pa logično je kad imaš (-1)^n u nizu da razdvojiš na dva slučaja. Prvi kad je n paran broj tj. n=2k, k=1,2,3,... i kad je n neparan broj tj. n=2k-1, k=1,2,3,... . Drugo će ti biti jasno posle prvog. Ograničen je odozgo sa 3, jer za ma koje n (n-prirodan broj) tvoj niz  , neće preći 3. , neće preći 3.Odozdo jer nikad neće biti manji od nula. Poželjno je uvek uprostiti opšti član, tako da se jasno vidi šta je maksimum ili minimum odnosno inf i sup, jer ne smeš da koristiš izvode. Što se nejednakosti tiče, uvek možeš iskoristi neku nejednakost da bi "olakšao sebi život". [ patkan1992 @ 09.12.2011. 16:42 ] @
Do poslednjeg razumem. A poslednje: kako da znam koju nejednakost smem da uzmem?
[ SrdjanR271 @ 09.12.2011. 16:48 ] @
[ patkan1992 @ 09.12.2011. 17:18 ] @
[ SrdjanR271 @ 09.12.2011. 17:23 ] @
[ SrdjanR271 @ 09.12.2011. 17:35 ] @
[ patkan1992 @ 09.12.2011. 17:43 ] @
Onda nisam dobro razumeo ovo:
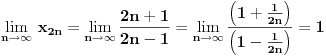 Ti si ovde i gonju i donju podelio sa  , zar ne? I odakle ti iz poslednjeg izraza da je jednako 1? , zar ne? I odakle ti iz poslednjeg izraza da je jednako 1?I sada ovo sto mi kazes da sam pobrkao sa limesima, znaci ovde ne vaze ista pravila kao god granicne vrednosti funkcije? Ne smem da delim brojem koji ima najveci izlozilac? [ SrdjanR271 @ 09.12.2011. 17:53 ] @
Citat: patkan1992: Onda nisam dobro razumeo ovo: 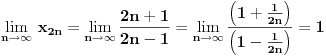 Ti si ovde i gonju i donju podelio sa  , zar ne? I odakle ti iz poslednjeg izraza da je jednako 1? , zar ne? I odakle ti iz poslednjeg izraza da je jednako 1?I sada ovo sto mi kazes da sam pobrkao sa limesima, znaci ovde ne vaze ista pravila kao god granicne vrednosti funkcije? Ne smem da delim brojem koji ima najveci izlozilac? Tačno je da sam delio sa 2n (ili "izvukao" 2n). Ali ja imam tu količnik, a ti imaš samo 2n+1. Obnovi malo najobičnije limese. [ patkan1992 @ 09.12.2011. 18:00 ] @
[ SrdjanR271 @ 09.12.2011. 18:10 ] @
Najbolje ti je u početni jer kao što sam napisao {0, 3, 0.5, 1.66667, 0.666667, 1.4, 0.75, 1.28571, 0.8, 1.22222, 0.833333, 1.18182, 0.857143, ...}.
Snimi kako ide 0<3>0.5<1.6...... Za monotonost (rast) treba ili <= <= <= <= , ili < < < < < < . Za opadanje monotono treba >>>>>>>> i >= >= >= ..... Znači da je svaki sledeći veći ili da je svaki sledeći manji. Mi imamo "Mix". Pa zato nije ni rastući ni opadjući. Kad je samo >>>>> ili <<<<<< kažemo da strogo opada (raste). A to za 1 ili -1: Odgovor je 1. [ patkan1992 @ 09.12.2011. 18:16 ] @
Aham, kapiram sada. Hvala :)
Ne znam da l si napisao nesto posle ovih dveju tacaka, ali nije mi izbacilo nista. Pa ako bi mogao da ispravis? [ Nedeljko @ 09.12.2011. 18:24 ] @
Mislim da bi najbolje bilo da sad kad misliš da si shvatio uradiš ovde samostalno neki zadatak, pa da mi to proverimo.
[ SrdjanR271 @ 09.12.2011. 18:28 ] @
[ SrdjanR271 @ 09.12.2011. 18:31 ] @
Citat: Nedeljko: Mislim da bi najbolje bilo da sad kad misliš da si shvatio uradiš ovde samostalno neki zadatak, pa da mi to proverimo. Slažem se. Evo ova tri mi je dužan osto :) http://www.elitesecurity.org/p3007677 Edit: Nemoj da žuriš! [ patkan1992 @ 09.12.2011. 18:50 ] @
[ SrdjanR271 @ 09.12.2011. 19:03 ] @
[ patkan1992 @ 09.12.2011. 19:14 ] @
[ patkan1992 @ 09.12.2011. 19:21 ] @
[ SrdjanR271 @ 09.12.2011. 19:29 ] @
Po meni je ovo dobar primer.
Niz sin(n) je ograničen odozgo sa 1, odozdo sa -1, nije konvergentan, nije monoton. 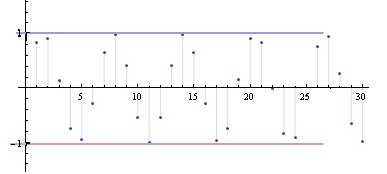 Idem sad da puštam mužiku, na eventualna pitanja ću odgovoriti stura ili kasno noćas. [ patkan1992 @ 09.12.2011. 19:34 ] @
Zanima me kako se jos gleda ova ogranicenost sada? U kom izrazu gledam? Je l za oba ova podniza posebno, ili kako?
[ patkan1992 @ 09.12.2011. 19:43 ] @
To razumem. Ali pitam za ovaj moj primer sto sam uradio, nekoliko posta iznad Sonec.
Gde gledam ogranicenost, da li u ovim podnizovima ili u pocetnom izrazu niza? [ Sonec @ 09.12.2011. 19:48 ] @
Pa mozes da gledas na podnizovima, pa onda uzmes minumum donjih ogranicenja ta dva podniza, i to ti je donje ogranicenje pocetnog niza, a maksimum gornjih ogranicenja ti je gornje ogranicenje pocetnog niza. Il gledas odjednom ceo niz, pa tu vidis. Zavisi sve od situacije.
[ patkan1992 @ 09.12.2011. 19:59 ] @
Ok, hvala :) Mnogo ste mi pomogli!
[ Sonec @ 09.12.2011. 21:49 ] @
Citat: Citat: Aj Milose, odgovori na ovo pitanje. EDIT: vidim da si vec nesto odgovorio, al mislim da je ovo bolji odgovor: posto su granicne vrednosti (tacke nagomilavanja) ova dva podniza medjusobno razlicite, onda mozemo da kazemo da je nas niz divergentan. [ patkan1992 @ 09.12.2011. 22:07 ] @
Sada sam se opet zbunio ovim tvojim pitanjem. Tj. pogledao sam opet ovo sto sam radio oko ovog niza. I je l je tacno da je ogranicen sa 1?
[ Sonec @ 09.12.2011. 22:33 ] @
Jeste, tacno je. Al mislim da ti je bitnije ono sto sam ti napisao za divergenciju (to moras da znas).
[ ConfusingThings @ 22.12.2011. 23:40 ] @
Da li bi mogao neko da i objasni resenje zadatka:
Ispitati konvergenciju niza 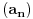 ciji je opsti clan zadat sa: ciji je opsti clan zadat sa: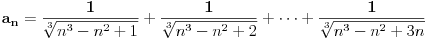 e sad... znam da se radi preko teoreme o tri niza.. tj nadju se 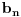 i i 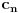 takvi da je takvi da je 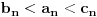  i 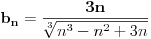 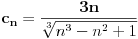 zatim 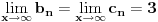 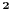 i iz 1 i 2 sledi da je niz  konvergentan ida je konvergentan ida je 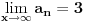 nisu mi jasni b i c, kako se do njih doslo..? 3n u brojiocu predstavlja broj sabiraka u a (jel tako? :/), ali kako se dobijaju imenioci? da li je slucajno to sto se imenilac niza b poklopio sa imeniocem poslednjeg u a, a imenilac niza c sa prvim u a, ili je to uvek (mogu li tako da se traze dva niza za teoremu - preko 'formule'?)?? [ Sonec @ 23.12.2011. 00:02 ] @
[ ConfusingThings @ 23.12.2011. 01:41 ] @
Hvala puno
[ miki069 @ 26.12.2011. 17:01 ] @
@Patkan1992:
Ostavi za sada po strani mootone i ograničene nizove. Ako hoćeš nešta da uradiš idi sledećim redosledom: 1. Nauči rešavanje limesa 2. Aritmetička, geometrijska, harmonijska sredina i nejednakosti između njih. 3. Binomna formula 4. Bitne nejednakosti 5. Faktorijel i veze između faktorijela 6. Definicija niza 7. Definicija tačke konvergencije, tačke nagomilavanja i razlike između istih. 8. Uradi što više primera dokazivanja konvergencije niza po defiiciji. 9. Definicije broja e. 10. Tek onda: teorema o monotonim i ograničenim nizovima, Košijev princip konvergencije nizova... Nemoj da shvatiš post kao zlonameran, jer čekaju te sledeće Analize (Matamatike) i sa njima: numerički redovi, funkcionalni nizovi i funkcionalni redovi. Veruj mi da sam potošio kilometre živaca da nekima objasnim razliku između obične i uniformne konvergencije funkcionalnih nizova (redova). Kada sam shvatio da ne razumeju konvergenciju numeričkih nizova, bilo mi je mnogo lakše. Možeš sa još 10 dobrih primera, metodom prepoznavanja, da napribirčiš da položiš Analizu 1 (ili Matematiku 1). Posle u Analizama (Matematikama) 2, 3 i 4 nećeš znati šta te snašlo. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|