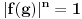
b) Stoga, ako je red elementa , onda je , pa je , odnosno .

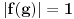
a) Prvo dokaži da je slika tog homomorfizma konačna podgrupa multiplikativne grupe kompleksnih brojeva. Zatim dokaži da postoji primitivni koren iz jedinice takav da su elementi slike tačno njegovi stepeni. Onda dokaži da je suma elemenata slike jedinica u trivijalnom slučaju, odnosno nula u netrivijalnom. Zatim dokaži da se u svaki element slike slika isti broj elemenata domena.