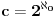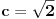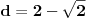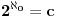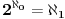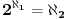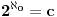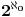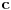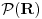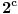|
|
[ CombatJazz @ 29.12.2011. 23:24 ] @
|
| Ako su a i b racionalni brojevi, onda je i (a+b)/2 racionalan broj koji se nalazi na sredini otvorenog intervala [a,b]. Nadalje, unutar toga intervala postoje dva racionalna broja i postoji opet neki racionalan broj koji se nalazi na sredini toga intervala. I takvih brojeva ima beskonačno mnogo i kažemo da je skup racionalnih brojeva gust jer svaki, koliko god mali interval, sadrži beskonačno mnogo racionalnih brojeva.
Neka su c i d iracionalni brojevi, te (c+d)/2 iracionalan broj koji se nalazi na sredini otvorenog intervala [c,d]. Analogno s racionalnim brojeva, i iracionalnih brojeva ima beskonačno mnogo na koliko god malom intervalu.
E sad mene zanima, koji je skup od ta dva gušći, tj. veći? Ili su oba jednaka? |
[ SrdjanR271 @ 29.12.2011. 23:53 ] @
Nisam neki poznavalac ove problematike.
Znam da racionalnih brojeva ima prebrojivo mnogo, a iracionalnih brojeva neprebrojivo mnogo.
Skup Q ima istu kardinalnost kao skup N.
Skup iracionalnih ima istu kardinalnost kao R.
http://operator.pmf.ni.ac.rs/w...%201%20sveska%201-2/mii1-5.pdf
http://en.wikipedia.org/wiki/Cardinality_of_the_continuum
[ darkosos @ 30.12.2011. 07:37 ] @
Da, pritom, sto je sada jasno, opisani postupak trazenja sredine nije dovoljno dobar da odvoji ove dve vrste "gustine". Stavise, takav postupak je prebrojiv, tj moze da se indeksira prirodnim brojevima.
[ petarm @ 30.12.2011. 08:51 ] @
U matematici se uvodi ekvipotentnost skupova. Ja to davno nisam citao, ali koliko se secam skupovi brojeva su ekvipotentni (imaju isti kardinalni broj) akko se izmedju ta dva skupa moze uspostaviti bijekcija. Za konacne skupove kardinalni broj je broj elemenata skupa, a za beskonacne skupove se uvode tzv. prebrojivo beskonacni skupovi. Njihov kardinalni broj je  i neprebrojivo beskonacni skupovi njihov kardinalni broj je 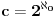 . Meni je jedno od ispitnih pitanja na 1. godini studija na algebri bilo da dokazem da je R neprebrojiv. Koristili smo na faxu Kantorov postupak. Znaci treba samo naci neku funkciju koja je bijekcija izmedju skupa racionalnih brojeva i celih i znaces da neprebrojivost R potice od iracionalnih brojeva. [ Bojan Basic @ 30.12.2011. 09:42 ] @
Citat: CombatJazz:
Neka su c i d iracionalni brojevi, te (c+d)/2 iracionalan broj
Ovo nije tačno (kontraprimer: 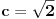 , 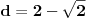 ).
Citat: petarm:
...i neprebrojivo beskonacni skupovi njihov kardinalni broj je 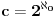 .
Pero, pazi bre šta pričaš.  Beskonačan skup je neprebrojiv (po definiciji) ako nije prebrojiv. O njegovom kardinalnom broju možemo reći samo da je veći od  , a takvih kardinalnih brojeva ima mnooogo (tj., ni slučajno 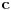 nije jedina mogućnost). [ Nedeljko @ 30.12.2011. 09:42 ] @
Aritmetička sredina dva iracionalna broja ne mora biti iracionalan broj.
Međutim, u svakom intervalu koji ima više od jedne tačke ima iracionalnih brojeva.
[ darkosos @ 30.12.2011. 10:08 ] @
Da, mogao bi se primer sa pocetka preformulisati i reci da oba skupa (sa relacijom poredjenja) imaju osobinu da izmedju svaka dva razlicita elementa postoji bar jedan element tog skupa.
Naravno, posto skup iracionalnih nije bas neka struktura, nije zatvoren za sabiranje itd., onda se trazenje tog "izmedju" elementa ne moze uraditi tako elementarno kao kod skupa racionalnih.
Ali poenta je u tome da ova osobina garantuje samo najmanje prebrojivost, rekao bih. Dakle ovakav skup ne moze biti konacan.
[ petarm @ 30.12.2011. 15:07 ] @
Citat: Bojan Basic: Pero, pazi bre šta pričaš.  Beskonačan skup je neprebrojiv (po definiciji) ako nije prebrojiv. O njegovom kardinalnom broju možemo reći samo da je veći od  , a takvih kardinalnih brojeva ima mnooogo (tj., ni slučajno 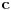 nije jedina mogućnost).
Moja greska. Zato si tu da me ispravis  Nisam siguran morao bih da pogledam, ali mislim da je cak na Algebri koju sam ja radio na 1. godini profesor koji mi je predavao napisao 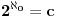 . A mozda je cak ovo upotrebljeno i u Algebri 1 Branimira Seselje, za to sam cak manje siguran. Ja sam video na nekim mestima da se pise 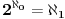 , 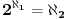 ... ali nisam bas skontao kako pravite tu razliku izmedju neprebrojivih skupova pa nisam ni ulazio detaljno u to. To se valjda zovu ordinali, je li? [ petarm @ 30.12.2011. 15:17 ] @
Da stoji u Algebri 1 kod Branimira Seselje na dnu strane 134., a takodje i na strani 124., a i isti oblik 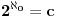 stoji i u mojoj svesci iz Algebre sa predavanja  [ Bojan Basic @ 30.12.2011. 15:25 ] @
Dobro stoji u Algebri 1 i u tvojoj svesci, stvarno važi 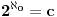 . Poenta je što 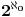 (tj. 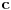 ) nije jedini kardinal veći od  .
Citat: petarm:
Ja sam video na nekim mestima da se pise 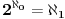 , 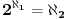 ...
Ovo važi samo pod uopštenom hipotezom kontinuuma (inače ne mora važiti). [ petarm @ 30.12.2011. 19:21 ] @
Nisam mislio da ciljas na to. Zanimljivo. Ako nije suvise komplikovano da li bi mogao da mi das primer neprebrojivog skupa koji ima razlicitu kardinalnost od 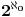 ?
[ CombatJazz @ 30.12.2011. 19:26 ] @
Da li možemo reći da skup racionalnih brojeva ispunjava sve aksiome realnih brojeva osim aksioma potpunosti?
Recimo imamo skup S {x € Q : x^2 < 3} tj. (-sqrt(3), sqrt(3)) presjek Q koji je omeđen, ali nema supremum u skupu racionalnih brojeva, već realnih. Da li se iz toga može zaključiti da je card(Q) < card(R)?
[ Bojan Basic @ 30.12.2011. 20:01 ] @
@petarm:
Skup 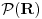 ima kardinalnost 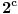 (tj. 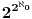 ). To je, naravno, više od 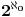 .
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|