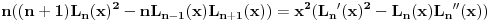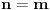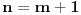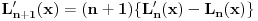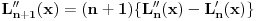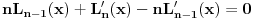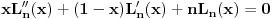Probaj indukcijom.

Dokaz zavisi od izbora definicije Lagerovih polinoma.

Ne razumem Nedeljko sta hoces da kazes? Mene jedino ovde brine za koje - ove ovo vazi. Verovatno vazi za vece ili jednako on nekog koje nije jedan, odnosno trebalo bi da bude dato u samom zadatku.

Lagerovi polinomi su definisani Rodrigovom formulom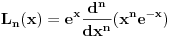



Pa je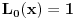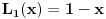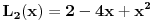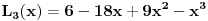





...

_{[Ovu poruku je menjao petarm dana 09.01.2012. u 16:00 GMT+1]}

krenuo sam indukcijom. vazi kad je n=1 i 2. kasnije se izrazi zapetljaju tako da opet ne ide...

Kasnije bi trebalo da pretpostavis da ovo vazi za . To ti je indukcijska hipoteza i onda koristeci to da dokazes da vazi za . Probaj to pazljivo da raspises. U tom poslednjem koraku ces verovatno trebati da koristis neku od rekurentnih relacija.

problem je sto mi ne pomaze ni jedna rekurenntna relacija u tom poslednjem koraku, a probao sam da kombinujem nekoliko. mozda ima nekih meni nepoznatih relacija...

Neke od relacija koje bi mogle biti korisne su









Pomuci se sada malo.

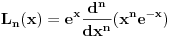To je jedan od ekvivalentnih načina definisanja. Nije problem da se iz te definicije (ili bilo kioje druge) izvedu sve ostale osobine, ali se mora znati od čega se polazi. Ovde imaš nekoliko načina definisanja

http://en.wikipedia.org/wiki/Laguerre_polynomial

Ti drugacije definisani Lagerovi polinomi su asocirani ili generalisani Lagerovi polinomi. Ovde na wikipediji oni definisu na pocetku normirane Lagerove polinome. Relacija ortogonalnosti za Lagerove polinome je



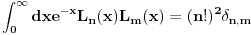Kada se Rodrigova formula definise kako je definisana na wikipediji Lagerovi polinomi su ortonormirani. Kada se tako definisu mi ih u fizici zovemo normiranim Lagerovim polinomima.

Inace ni u jednoj matematickoj knjizi nisam nasao da ove normirane Lagerove polinome zovu Lagerovim polinomima. Takodje ni u jednoj knjizi iz fizike. Pod Lagerovim polinomima smatraju se polinomi koji su definisani Rodrigovom formulom koju sam napisao gore.
<sub>[Ovu poruku je menjao petarm dana 09.01.2012. u 22:32 GMT+1]

[Ovu poruku je menjao petarm dana 09.01.2012. u 22:33 GMT+1]</sub>

Ti Lagerove polinome dobijas iz



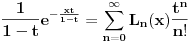gde je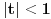

Leva strana jednakosti je tzv. funkcija generatrise za Lagerove polinome. Ovoj definiciji ekvivalentna je Rodrigova formula koju sam ja napisao, a ne ona koja stoji na wikipediji.

Ovde na wikipediji se radi pozivanje na kvantnu. U kvantnoj skalarni proizvod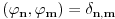



ima smisao verovatnoce ako 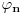ima smisao funkcije stanja. Zato je bitno da bude normiran. U problemu atoma vodonika - Sredingerova jednacina dobijaju se kao resenja Lagerove funkcije i otuda cela ova prica na wikipediji.

Kao što i sam vidiš, postoji više načina definisanja Lagerovih polinoma. Naveo si dva - preko Rodrigove formule i preko funkcije generatrise. Može i preko težinske funkcije, pa biraj ago šta ti drago da bude norma Lagerovih polinoma.

Recimo da sam izabrao ovu Rodrigovu formulu za definiciju od Ln. Kako se tada dokazuje?

Radeci sa ovom Rodrigovom formulom koju je Nedeljko okacio to nije identitet, sto ti pokusavas da dokazes.

zasto nije ako su ekvivalentne?

Za ovu definiciju Lagerovih, koju je Nedeljko napisao, jednostavno vaze skroz drugacije relacije za iste. Ako primetis u obe definicije samo su jednaki Lagerovi polinom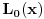i i 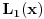. Ova definicija koju sam ja napisao je onako kako sam ja ucio na faxu da se definisu Lagerovi polinomi. Tako ih je definisao Mitrinovic. Tako ih je definisao Aljancic npr. od nasih autora. Od svetskih u knjigama koje sam ja gledao iz Specijalnih funkcija definisani su na takav nacin. Ako koristis takvu definiciju mozes imati veci dijapazon knjiga iz kojih mozes uzimati neke identitete, rekurentne relacije i slicno. Ne postoji medjutim ni prepreka da ti definises ovako kako stoji na wikipediji. Na Matematickoj fizici 2 u Novom Sadu mi smo, opet ponavljam, tako definisane Lagerove polinome zvali normirani Lagerovi polinomi.

_{[Ovu poruku je menjao petarm dana 10.01.2012. u 22:11 GMT+1]}