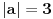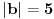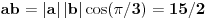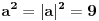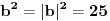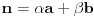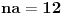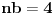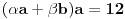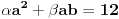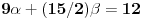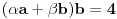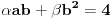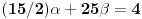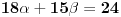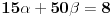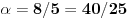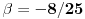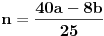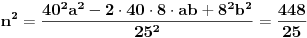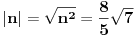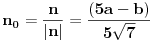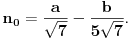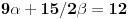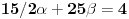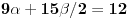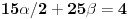[ Vasolino @ 11.01.2012. 01:20 ] @
| Moze li neko da mi pomogne oko ovoga,vrtim se u krug,iskren da budem...Naći jedinični vektor n0,komplanaran sa vektorima a i b ako važi sledeće:skalarni proizvod n*a=12,skalarni proizvod n*b=4,intenziteti a i b su 3 i 5 respektivno a ugao koji oni zaklapaju međusobom iznosi -Pi/3.E sada,zadatak sam radio na sledeći način,inače...Iz uslova komplanarnosti,kažem da su vektori linearno zavisni tj. da se vektor n može zapisati preko vektora a i b.Iskoristim tri skalarna proizvoda,koja su mi data,n*a.n*b,i izračunam a*b,na taj način nađem koeficijente proporcionalnosti,koji mi kažu u kojoj su vezi,vektori n,a i b ( n=-1.6*a+0.32*b),interesuje me da li postoji način da ja izračunam koliko tačno iznose,koordinate vektora,a i b,ili rezultat ostaje tako u opštim brojevima.Čini mi se da sam uzeo sve date uslove u obzir,i tako mi rezultat ostaje u opštim brojevima,izražen preko koordinata vektora a i b.Hvala unapred,svima. |