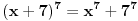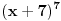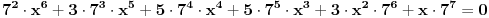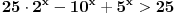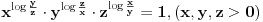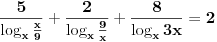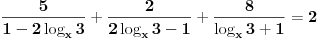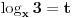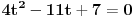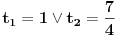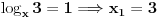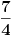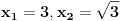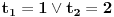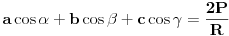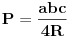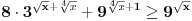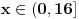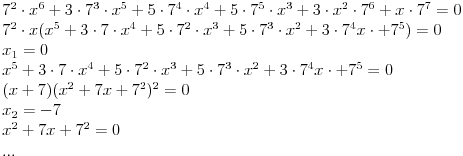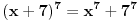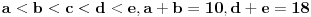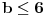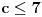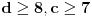[ Sherlock Holmes @ 12.01.2012. 12:03 ] @
|
[ vukadinovic.i @ 12.01.2012. 13:07 ] @
Na brzinu...
2. zadatak: 2x=a, 5x=b, 25a-ab+b-25>0 (a-1)(25-b)>0, odavde se lako resava x1=0 i x2=2... [ Sherlock Holmes @ 12.01.2012. 13:58 ] @
Citat: vukadinovic.i: Na brzinu... 2. zadatak: 2x=a, 5x=b, 25a-ab+b-25>0 (a-1)(25-b)>0, odavde se lako resava x1=0 i x2=2... Hvala! Nisam se toga setio. Citat: edisnp: Kod ovog sedmog mislim da ti samo fali jos uglasta zagrada,( 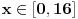 ). ).Da,da... Greska! Hvala! Citat: Hvala! Nisam znao ovaj izraz 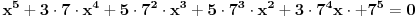 da napisem u obliku proizvoda. Dosao sam do njega i dobio da je da napisem u obliku proizvoda. Dosao sam do njega i dobio da je 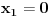 , al' dalje nisam znao... , al' dalje nisam znao... [ darkosos @ 12.01.2012. 20:28 ] @
[ Sonec @ 12.01.2012. 20:43 ] @
3. Samo logaritmuj, tvrdjenje posle trivijalno sledi.
[ darkosos @ 12.01.2012. 20:55 ] @
Cini mi se da onda u postavci nesto nije dobro, kada zamenis 3 u polaznu jednacinu, ne dobijes 2 nego 1.
+ za 3. probaj da logaritmujes levu stranu, trebalo bi da se sve pokrati i da dobijes nulu, pa je onda argument jednak 1. Sad sam video da je Sonec bio brzi, al' eto... :) [Ovu poruku je menjao darkosos dana 12.01.2012. u 22:12 GMT+1] [ Sherlock Holmes @ 12.01.2012. 22:13 ] @
[ SrdjanR271 @ 12.01.2012. 23:58 ] @
Za 5-i, mozda nesto ovako:
http://www.goiit.com/posts/lis...a-sinbsinc-1056850.htm#1347534 Preko sinusne teoreme. [ rudy_kv @ 13.01.2012. 13:25 ] @
6. Zadatak
I ja dobijam da je zbir 35 odnosno da zadaci nose (redom po tezini): 4, 6, 7, 8 i 10 poena [ edisnp @ 13.01.2012. 13:33 ] @
[ darkosos @ 16.01.2012. 07:55 ] @
5. Sam resio na "geometrijsku" nacin; ideja je da se primeni nesto slicno kao kada se dokazuje sinusna teorema:
Prvo pretpostavimo da je trougao ostrougli; tada je centar opisane kruznice O u unutrasnjosti trougla; ako iz ove tacke povucemo visine na stranice, npr hOa, hOb i hOc, tada imamo: 1) 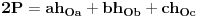 i i 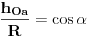 i slicno za ostale stranice i uglove. i slicno za ostale stranice i uglove.Ovo drugo je posledica toga da je ugao BOC centralni nad tetivom BC sa perifernim uglom BAC tj alpha, pa je jednak 2 alpha. Ako je A' podnozje visine iz O na stranicu a, onda je ugao A'OB=A'OC (jer je trougao jednakokraki OB=OC=R), pa je njegova polovina 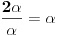 Kada 1) podelis sa R dobijas tacno to sto ti treba. Ako trougao ima tup ugao, npr u C, onda je povrsina trougla 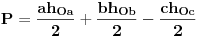 . Uz to da je . Uz to da je 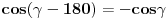 , opet se moze dobiti trazeni rezultat... , opet se moze dobiti trazeni rezultat...Ako je trougao pravougli, onda je kao u prvom slucaju, samo je jedan od clanova zbira, tj. jedna visina i jedan cos, jednak 0. [ scale5 @ 04.01.2013. 17:28 ] @
Da li na takmicenju dolaze nagradni zadaci iz Tangente ili neki drugi? U pitanju je 1. razred spec. matematickog odeljenja
Hvala unapred [ Nedeljko @ 04.01.2013. 22:53 ] @
Nemoj ni pomisliti da dolaze zadaci iz neke zbirke/časopisa.
[ igorpet @ 04.01.2013. 23:13 ] @
...
 [ Bojan Basic @ 04.01.2013. 23:13 ] @
Zapravo, na nižim nivoima takmičenja dolaze, i to po tačno utvrđenom kriterijumu: dva zadatka na Opštinskom takmičenju, jedan zadatak na Okružnom takmičenju, iz časopisa „Tangenta“ iz tekuće i prethodne dve godine. To nije nikakva tajna, i u zvaničnim rešenjima se uredno naznači koji su to zadaci i odakle su tačno uzeti (iz kog broja i iz koje rubrike).
Odgovor za člana scale5: dolazi u obzir bukvalno bilo šta što je objavljeno u „Tangenti“. Znači, ne samo nagradni zadaci, već i zadaci koji se pojave na bilo kom drugom mestu u časopisu, pa čak i npr. zadaci koji su dati u sklopu nekih članaka. [ Sherlock Holmes @ 11.01.2013. 21:12 ] @
Obrati paznju i na zadatke sa korica. Prosle godine je bio na okruznom takmicenju(B kategorija) jedan od zadataka iz Tangente upravo sa korica. :) Trebale su da se nadju tezine nekih tegova na razlicitim nivoima.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|