[ Nedeljko @ 16.01.2012. 18:28 ] @
|
[ Bojan Basic @ 16.01.2012. 23:51 ] @
Citat: Prema ovom izvoru, Ojler je dokazao samo za  i i 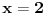 , a uopštenje za racionalne brojeve dokazao je Lambert: , a uopštenje za racionalne brojeve dokazao je Lambert:Citat: In a paper presented to the Berlin Academy in 1768 Lambert showed that, if x is a nonzero rational number, then neither e ^x nor tan x can be rational. Citat: Ovaj izvor navodi da je prvi dokaz Ležandrov: Citat: Adrien-Marie Legendre (1794), after introducing the Bessel–Clifford function, provided a proof to show that π2 is irrational [ Nedeljko @ 17.01.2012. 14:14 ] @
Pišem neki članak o dokazima iracionalnosti, koji bi se mogao pratiti sa gimnazijskim znanjem matematike i koji bih okačio negde na internet, kako bi se ovo znanje popularisalo.
Predznanje koje očekujem od čitaoca su osnovne osobine deljivosti (uključujući osobine uzajamno prostih brojeva i teoremu o euklidskom delenju), osnovne osobine limesa, izvoda i integrala. Za sada sam napisao zajedno sa dokazima potrebnih pomoćnih stavova 1. Potreban i dovoljan uslov da je broj  iracionalan, gde su iracionalan, gde su  i i  pozitivni racionalni brojevi i pozitivni racionalni brojevi i  . .2. Potreban i dovoljan uslov da je broj 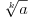 iracionalan, kde je iracionalan, kde je 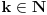 i i  pozitivan racionalan broj. pozitivan racionalan broj.3. Metod za dokazivanje iracionalnosti brojeva kao što su  . .4. Iracionalnost broja  kao i brojeva oblika kao i brojeva oblika 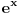 za za  , odnosno brojeva , odnosno brojeva  gde je gde je  pozitivan racionalan broj različit od 1. pozitivan racionalan broj različit od 1.5. Iracionalnost broja 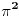 i samim tim broja i samim tim broja  . .6. Iracionalnost kvadrata trigonometrijskih funkcija za vrednosti argumenata koje su racionaljne i različite od nule i inverznih trigonometrijskih funkcija za vrednosti argumenata čiji su kvadrati racionalni brojevi različiti od nule. 7. Isto kao pod 6, samo za hiperboličke i inverzne hiperboličke funkcije. Planiram da dodam: 8. Osobine racionalnih i iracionalnih brojeva kao što su (ne)periodičnost decimalnog zapisa, (bes)konačnost verižnog razvoja i teorema da ako je  proizvoljna racionalna funkcija sa racionalnim koeficijentima i proizvoljna racionalna funkcija sa racionalnim koeficijentima i 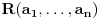 iracionalan broj, onda je bar jedan od brojeva iracionalan broj, onda je bar jedan od brojeva  iracionalan. iracionalan.9. Veza između funkcija i njihovih inverza. Primera radi, stavovi da su brojevi oblika 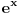 za za  i i  za pozitivno racionalno za pozitivno racionalno 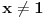 su ekvivalentni. su ekvivalentni.10. Uopštenje tačke 2 na brojeve oblika 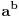 gde su gde su  i i  racionalni brojevi. racionalni brojevi.11. Dopunu tačke 3 do metoda kojim se za svaki broj koji je izražen proizvoljno složenim konačnim izrazom u kome učestvuju celobrojne konstante i operacije sabiranja, oduzimanja, množenja delenja i korenovanja proizvoljnog stepena u konačnom broju koraka utvrđuje da li jeracionalan (i ako jeste koji) ili iracionalan. Postupak bi bio uopšten i na izraze u kojima se pojavljuju konstante koje su algebarski brojevi dati polinomima koji ih poništavaju i lokalizacijama (kojima se razlikuju od ostalih korena). 12. Pojmovima algebarskih i transcedentnih brojeva i osobinama kao na primer da algebarski brojevi čine polje i da su zatvoreni za korenovanje, a transcedentni za stepenovanje i korenovanje, kao i sabiranje, oduzimanje, množenje i delenje algebarskim brojevima različitim od nule. Pojam algebarski nezavisnog skupa brojeva. 13. Konstrukcija transcedentnih brojeva Kantorovim dijagonalnim postupkom i beskonačnih algebarski nezavisnih skupova istom metodom. 14. Liuvilova teorema i opšti postupak konstrukcije transcedentnih brojeva njenom primenom. 15. Transcedentnost broja  . .16. Lindemanova teorema i Lindeman-Vajerštrasova teorema bez dokaza i posledice. Skica veze sa nemogućnošću kvadrature kruga lenjirom i šestarom. 17. Geljfand-Šnajderova teorema bez dokaza i posledice. [ igorpet @ 17.01.2012. 16:43 ] @
Pogledaj u ovoj knjizi Mathematics and Its History John Stillwell (2002)
Kada sam nesto ja trazio cini mi se da je bilo interesantnih delova o iracionalnosti. Mathematics and Its History John Stillwell [ Sini82 @ 18.01.2012. 12:10 ] @
Nedeljko, svaka čast na uloženom trudu. Obavezno postavi link ovdje prema članku, ako nije problem? Unaprijed hvala.
[ Nedeljko @ 18.01.2012. 14:38 ] @
Ne znam koliko je interesantna trenutna radna verzija, ali predstavlja zaokruženu celinu, pa je ovde postavljam. Možda nije loše zbog primedbi, kako bi se tekst učinio boljim.
[ Sini82 @ 19.01.2012. 13:03 ] @
Pregledao sam, zaključno sa dokazom teoreme 7. Kada (ako) budem imao vremena analiziraću rad do kraja. Dopada mi se ideja i rad.
1. Zašto u formulaciji Bernulijeve teoreme ne uzmeš uslov 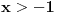 ? Koja je svrha dogovora ? Koja je svrha dogovora 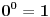 ? Kako ga opravdavaš? Mislim da je on u radu suvišan i bez njega sve funkcioniše. ? Kako ga opravdavaš? Mislim da je on u radu suvišan i bez njega sve funkcioniše.2. U dokazu teoreme 5. ako je 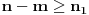 onda je onda je  , tj odmah nakon prvog , tj odmah nakon prvog 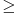 možeš da pređeš na možeš da pređeš na  . .3. U dokazu teoreme 7. ne bih uvodio novu oznaku 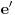 , ostao bih na staroj oznaci , ostao bih na staroj oznaci  , gimnazijalcima kojima si namijenio rad to ne bi trebao da predstavlja problem (vidim da u dokazima puno ne detaljišeš, podrazumijevaš im solidno predznanje). , gimnazijalcima kojima si namijenio rad to ne bi trebao da predstavlja problem (vidim da u dokazima puno ne detaljišeš, podrazumijevaš im solidno predznanje).[Ovu poruku je menjao Sini82 dana 19.01.2012. u 14:50 GMT+1] [ Nedeljko @ 19.01.2012. 16:30 ] @
1. Svrha konvencije
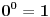 , koja se primenjuje na Bernulijevu nejednakost je da nejednakost važi za , koja se primenjuje na Bernulijevu nejednakost je da nejednakost važi za 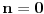 i i 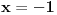 . Kada bi se tvrđenje formulisalo za . Kada bi se tvrđenje formulisalo za 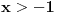 , kao što predlažeš, onda ta konvencija ne bi bila neophodna. Obzirom da mi ta nejednakost treba samo za , kao što predlažeš, onda ta konvencija ne bi bila neophodna. Obzirom da mi ta nejednakost treba samo za 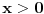 , predlog može da se uvaži. , predlog može da se uvaži.2. Izmenjeno na malo drugačiji način. Pogledaj. 3. Uvođenje nove oznake je obavezno, jer na tom mestu gde se ta oznaka uvodi nije jasno da li je to broj e, tj. to je ono što treba dokazati. Kada bi se koristila ista oznaka e, onda bi ispalo da treba dokazivati da je e=e, a jednakost nečega sa samim sobom je nešto što se ne dokazuje. Jednakost brojeva se ne može dokazivati uvođenjem iste oznake za njih. No, ta oznaka je korišćena samo u tom dokazu. Posle toga, kada je poznato da je suma tog reda jednaka e, oznaka e' se naravno više ne koristi. Evo nove verzije. [ Sini82 @ 19.01.2012. 17:00 ] @
Nedeljko, u pravu si za 3. Gore je u tvrđenju teoreme bilo n dole k, na to sam mislio ali to je uredno, nemam primjedbe (lapsus, do mene je).
Nezgodno je ovo 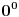 , zato me zanima. Cijelo vrijeme ih u školi uče da je taj izraz nedefinisan, nisu se nikad dosad sretali sa tom vrstom dogovora u matematici. Da li je tako nešto matematički korektno (mislim na , zato me zanima. Cijelo vrijeme ih u školi uče da je taj izraz nedefinisan, nisu se nikad dosad sretali sa tom vrstom dogovora u matematici. Da li je tako nešto matematički korektno (mislim na ; nije mi namjera da te kritikujem, ovo mi je posebno zanimljivo a možda i prilika da nešto naučim)? Kako se to opravdava? Možda je potrebno neko dodatno objašnjenje. ; nije mi namjera da te kritikujem, ovo mi je posebno zanimljivo a možda i prilika da nešto naučim)? Kako se to opravdava? Možda je potrebno neko dodatno objašnjenje.[ Bojan Basic @ 19.01.2012. 17:28 ] @
Citat: Sini82: Cijelo vrijeme ih u školi uče da je taj izraz nedefinisan, nisu se nikad dosad sretali sa tom vrstom dogovora u matematici. To je zato što slabo pratiš ovaj forum. Citat: Nedeljko: Pomenuti izraz nema definisanu vrednost u matematici jer ne postoji limes od xiy kada x teži nuli sa desne strane i y teži nuli na proizvoljan način. Ipak, to ne znači da nema smisla u konkretnoj situaciji uzeti da taj izraz ima određenu definisanu vrednost. Bitno je da se zna sadržaj teoreme, kao i da postoji dokaz iste u toj formulaciji. Nije ništa pogrešno u iskazu teoreme uzeti tako nešto po konvenciji (samo za iskaz teoreme i njen dokaz). Štaviše u teoriji skupova u kardinalnoj, kao i ordinalnoj aritmetici jeste 00=1. Često se i u aritmetici prirodnih, celih i racionalnih brojeva (dakle u teoriji brojeva), kao i u algebri (odnosno gde nemamo posla sa limesima) vrednost tog izraza uzima baš tako. U teoriji mere i integracije je na primer nula puta beskonačno jednako nuli. [ Sini82 @ 19.01.2012. 19:58 ] @
Hvala Bojane. Pratim forum, nije valjda za očekivati da svaki gimnazijalac koji čita rad takođe prati ovaj forum? Nije forum jedino mjesto na internetu gdje postoji objašnjenje zašto se uzima baš da je 0^0=1, nadao sam se da bih možda od vas ovdje na forumu naučio nešto novo što nisam pročitao na internetu. Primjedba se odnosila na sadržaj fusnote u radu. Moja sugestija je da se negdje u radu npr. u sadržaju fusnote to eksplicitno i navede.
Moje mišljenje je da ovakvu vrstu dogovora u matematici treba izbjegavati osim ako je to baš potrebno. Ovdje nije taj slučaj. Malo ko će doći u situaciju da mu takva formulacija Bernulijeve nejednakosti treba. [ Nedeljko @ 19.01.2012. 20:40 ] @
Nem gimnazijalac ne treba da bude upoznat sa tom konvencijom, niti da prati forum, već samo da je pročita u tekstu. Uz nju je kontekst stava bio potpuno određen. Takođe, konvencije se ne dokazuju i ne pravdaju. Konvencija je dogovor i kao takva ne može biti ni tačna ni netačna.
Realni i celobrojni stepen nisu ista operacija. U slučaju stepenovanja na celobrojni izložilac ima smisla uzeti da je 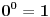 , dok u slučaju stepenovanja sa realnim izložiocem to svakako treba da bude nedefinisano. , dok u slučaju stepenovanja sa realnim izložiocem to svakako treba da bude nedefinisano.[ Sini82 @ 19.01.2012. 20:56 ] @
[ Sini82 @ 19.01.2012. 22:15 ] @
Pregledao sam, zaključno sa "Metod korena polinoma". Nisam kontrolisao stranu 7, vjerujem da nema računske greške, bitno je da je princip izložen kako treba.
4. Iznad teoreme 12. umjesto s(s,p) treba s(k,p). [ Nedeljko @ 21.01.2012. 01:07 ] @
Hvala! Evo ispravke.
[ Sini82 @ 21.01.2012. 21:38 ] @
Pregledao sam letimično rad do kraja, na str. 12. umjesto "Na sonovu teorema 9 i 5" treba "Na osnovu teorema 9 i 5". Bilo bi dobro da neko ko ima vremena detaljnije pregleda rad do kraja i potvrdi da nema grešaka.
Svaka čast, Nedeljko. Da li si mislio ubaciti u rad istorijski dio, svu tu priču oko dokaza iracionalnosti ili tako nešto? [ Nedeljko @ 21.01.2012. 23:23 ] @
Ne, istorijski deo me lično ne zanima. Raspitivao sam se oko tih podataka samo zbog citiranja autora (radi korektnosti), mada bih onda i pored dokaza trebao da ubacim čiji su (jer obično nisu navedeni oni istorijski prvi, pa da je autor dokaza isti kao autor teoreme).
Zamenio sam prilog uz prethodnu poruku novom verzijom, ali me je nažalost posao pritegao, tako da će rad na članku morati da pričeka nekoliko dana. [ Sini82 @ 22.01.2012. 12:30 ] @
Spominjao si popularizaciju znanja, zbog toga me je interesovalo. To bi čitaocu koji se prvi put sreće sa tim dokazima dalo neku opštu sliku i vremenski okvir u kome se sve to dešava. Ne bi bilo loše i napisati nešto o značaju tih dokaza u matematici.
Inače, može rad i ovakav da ostane, nemam zamjerki. Prethodna napomena je isključivo radi popularizacije znanja, da se čitalac motiviše (zainteresuje i pridobije) da uloži napor koji je potreban za praćenje rada. Hoćeš li ubaciti "Literatura", "Sadržaj" itd. ili će forma rada ostati ista? Dobro je što praviš pauzu nekoliko dana, nadam se da će za to vrijeme neko još provjeriti rad i potvrditi da nema grešaka. [ Sonec @ 22.01.2012. 13:36 ] @
Ma, dodavanje istorijskog dela je bespotrebno rekao bih. Rad treba da sadrzi izvesnu dozu ozbiljnosti, dovoljno je navoditi samo imena matematicara cija se tvrdjenja dokazuju/koriste/razmatraju (kao sto je Nedeljko i radio).
[ Nedeljko @ 22.01.2012. 16:07 ] @
Ne kažem da istorijski podaci nemaju vrednost, ali ja nisam zainteresovan da se time bavim. Kada se tekst nagoji, videću koliko strana ima, pa da vidim da li da promenim stil "article" u "book". U svakom slučaju će nešto što ima poveći broj strana imati sadržaj. Naravno, dobro je dati i reference.
[ Sini82 @ 22.01.2012. 23:48 ] @
Kada završiš, uradiš svih 17 stavki, možda proširiš sa još kojom u toku rada, biće sadržajan i po dosadašnjem sadržaju sudeći, kvalitetan rad. Pratiću verzije i trudiću se da budem što više od pomoći, naravno, onoliko koliko mi to obaveze dozvole. Biće to prava stvar.
[ Nedeljko @ 26.01.2012. 16:18 ] @
Društvo, moraću da vas razočaram. Nastavak će morati da pričeka još koji dan.
Šmrc! [ Nedeljko @ 03.03.2012. 23:34 ] @
Ugrabio sam nešto vremena da malo dopunim i ispravim članak. Evo nove verzije.
Što se oznaka verzija tiče, promena trećeg samo broja znači da su u pitanju samo ispravke grešaka, a povećanje drugog broja bez prvog znači da ima i nekih dopuna. Izmena prvog proja verzije označava završetak velike celine. [ darkosos @ 04.03.2012. 10:05 ] @
Nisam previse ulazio u same dokaze, verujem da su dobro pregledani :)
Ali jedna stilska stvar, a moze se reci i matematicka: u tvrdjenjima nekih teorema navodis skup u kome treba da se nadje promenljiva, kao npr. teorema 5, dok si negde to ispustio, kao npr teorema 2, 4 itd... To ne bi bilo lose da se nekako uskladi, ili da kazes da se odnosi na realne brojeve ako nije drugacije navedeno... I jos nesto, mozda vise kao sugestija: koristis termin "neparan prost broj" koji mi je nekako suvise rogobatan za cinjenicu da su to svi sem 2. Mozda je intuitivnije da se kaze prost broj veci od 2? Pretpostavljam da tako pises zbog T12 gde se pominju neparni brojevi? [ Nedeljko @ 31.08.2013. 18:54 ] @
Samo da okačim noviju verziju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|