[ ortodox888 @ 18.01.2012. 10:04 ] @
| Pokazati da za svaki prost broj p, grupa G reda 2p sadrzi bar jednu normalnu podgrupu reda p. Resenje potrebno hitno [Ovu poruku je menjao ortodox888 dana 18.01.2012. u 18:36 GMT+1] |
|
[ ortodox888 @ 18.01.2012. 10:04 ] @
[ Sonec @ 18.01.2012. 10:45 ] @
[ Nedeljko @ 18.01.2012. 11:02 ] @
Ne, Lagranževa teorema ne tvrdi da podgrupa reda koji je delitelj reda grupe postoji. Ona samo tvrdi da red podgrupe deli red grupe, tj. isključuje postojanje podgrupa čiji red ne deli red grupe. Teorema o postojanju podgrupa koja se ovde može primeniti je teorema Silova, ali ovo može i prostije.
Ako su svi elementi osim neutrala reda dva, onda je grupa komutativna, jer je 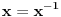 i samim tim i samim tim 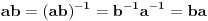 , a kod komutativnih grupa uvek postoji podgrupa čiji je red bilo koji željeni delilac reda grupe. U protivnom postoji element koji je delilac reda , a kod komutativnih grupa uvek postoji podgrupa čiji je red bilo koji željeni delilac reda grupe. U protivnom postoji element koji je delilac reda  ili ili 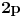 . .Normalnost se dokazuje baš kao što Sonec napisao. To je skica. Neka postavljač teme sam kompletira rešenje. Inače, nije zaslužio da mu se odgovori, kad je već u naslovu napisao da je zadatak "lak". [ ortodox888 @ 18.01.2012. 11:51 ] @
pa zar nije lak :D. Mene je najvise interesovalo kako se dokazuje da uopste postoji podgrupa reda p. Hvala Nedeljko.
[ Sonec @ 18.01.2012. 11:51 ] @
Hvala Nedeljko na ispravci.
Da li bi neko mogao meni da pomogne. Zadatak glasi: Neka su  i i  normalne podgrupe grupe normalne podgrupe grupe  takve da je takve da je 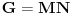 . Dokazite da je onda . Dokazite da je onda 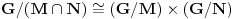 . .Jedino sto sam ja uspeo da uocim jeste 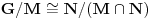 i slicno i slicno 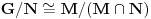 (koristeci prvu teoremu o izomorfizmu, ciji su uslovi ovde ispunjeni). Ali, ne znam kako bih mogao dalje da nastavim. (koristeci prvu teoremu o izomorfizmu, ciji su uslovi ovde ispunjeni). Ali, ne znam kako bih mogao dalje da nastavim.Postoji stav koji kaze: ako su 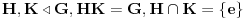 tada je tada je 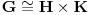 , mozda moze preko njega, al nzm kako. , mozda moze preko njega, al nzm kako.[ Nedeljko @ 18.01.2012. 14:01 ] @
Citat: ortodox888: pa zar nije lak :D. Ako je lak, onda si trebao da ga rešiš sam. Ovakvim procenama se unapred obezvređuje tuđi rad i zato takve stvari ne treba raditi. Odgovorio sam samo zbog Soneca, da bih ga ispravio, a inače ne bih sa onakvim stavom iz naslova. [ ortodox888 @ 18.01.2012. 17:47 ] @
Ja se izvinjavam ali stvarno nisam imao nameru da bilo čiji rad obezvredim mislio sam da ću time privući veću pažnju i ne znam već ni sam. Evo promenio sam naziv teme.
Elem imam problem, i ne samo ja već dosta kolega iz grupe, sa zadacima tipa ovog: Data je grupa reda 33 . Dokazati da ima bar jednu podgrupu reda 3 i reda 11 i da je ona jednaka proizvodu tih podgrupa. I dokazati da je ona ciklična. Zapravo meni najveći problem predstavlja da dokažem da te dve podgrupe komutiraju. [ Nedeljko @ 18.01.2012. 18:31 ] @
Ne znam da li ste učili teoreme Silova. Na osnovu njih je broj podgrupa reda 3 kongruentan jedinici po modulu 3 i deli 11, odakle postoji tačno jedna takva podgrupa, odnosno postoje tačno dva elementa reda 3 i oni komutiraju. Na sličan način se zaključuje da postoji tačno jedna podgrupa reda 11.
Izaberi jedan element a reda 3 i jedan element b reda 11. Koliki je red njihovog proizvoda? Ako je (ab)3=1, onda ab pripada istoj podgrupi reda 3, jer je takva podgrupa jedinstvena, pa i element b=a-1ab mora pripadati toj podgrupi, jer je ona jedinstvena. No, to nije moguće, jer je b reda 11. Na isti način se pobija mogućnost da je (ab)11=1, pa ab ne može biti reda ni 1, ni 3, ni 11, a mora pripadati skupu {1,3,11,33} jer mora da deli red grupe, pa je reda 33, to jest grupa je ciklična, pa samim tim i komutativna. [ ortodox888 @ 18.01.2012. 18:38 ] @
Nismo učili teoreme Silova. Ima li neki dokaz bez njega? I kako da dokažem da je proizvod tih podgrupa njihova grupa tj da je njihov proizvod uopšte grupa.
[ ortodox888 @ 18.01.2012. 19:07 ] @
Ako je (ab)3=1, onda ab pripada istoj podgrupi reda 3, jer je takva podgrupa jedinstvena, pa i element b=a-1ab mora pripadati toj podgrupi, jer je ona jedinstvena.
Zašto je ona jedinstvena? [ Nedeljko @ 18.01.2012. 20:24 ] @
Pa, napisao sam kako iz teorema Silova sledi jedinstvenost tih podgrupa. Teoreme Silova govore nešto o broju podgrupa tog reda. U ovom slučaju, broj podgrupa reda 3 mora biti delitelj broja 11 (dakle, u skupu {1,11}), a takođe mora biti kongruentan jedinici po modulu 3, pa je on jednak jedan.
Sonec, prema jednoj o teorema o izomorfizmima je 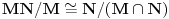 , pa treba dokazati da je , pa treba dokazati da je 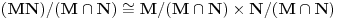 . .Presek podgrupa od kojih je bar jedna normalna je normalna podgrupa i tada je njihov proizvod podgrupa. Neka je 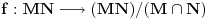 prirodni homomorfizam. Njegovo jezgro je tačno prirodni homomorfizam. Njegovo jezgro je tačno 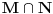 . Traženi izomorfizam biće preslikavanje . Traženi izomorfizam biće preslikavanje 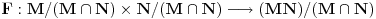 za koje je za koje je 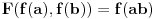 . Treba dokazati da je to preslikavanje korektno definisano. Ako je . Treba dokazati da je to preslikavanje korektno definisano. Ako je 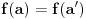 i i 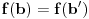 onda je onda je 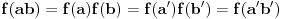 , odakle sledi korektna definisanost. Ostale neophodne osobine dokaži sam. , odakle sledi korektna definisanost. Ostale neophodne osobine dokaži sam.[ Nedeljko @ 19.01.2012. 01:48 ] @
Ako je p prost broj, onda su elementi reda p upravo elementi podgrupa reda p različiti od 1, a presek bilo koje dve podgrupe reda p sadrži samo neutral, pa je broj elemenata grupe reda p deljiv sa p-1.
Dakle, ako imamo m grupa reda 3 i n grupa reda 11, onda elemenata reda 3 i 11 ima 2m+10n. Ako ne bi bilo elemenata reda 33, onda bi osim neutrala svi elementi bili reda 3 ili 11, pa bi bilo 2m+10n=32, što je moguće samo za m=1 i n=2. Dakle, podgrupa reda 3 bi bila jedinstvena, dok bismo imali tačno dve podgrupe reda 11. Označimo podgrupu reda 3 sa A, a podgrupe reda 11 sa B i C. Proizvod bilo kog elementa podgrupe B različitog od 1 i bilo kojeg elementa podgrupe C različitog od 1 nije element nijedne od tih podgrupa, pa mora biti element skupa A\{1}. Za fiksirani element b skupa B\{1} preslikavanje skupa C\{1} u skup A\{1} definisano sa f(x)=bx ne može biti 1-1, pa neka je recimo bc=bc' za neke različite elemente c i c' skupa C\{1}. No, to je u suprotnosti sa aksiomama grupe, jer se množenjem jednakosti bc=bc' sleva sa b-1 dobija c=c'. Stoga pretpostavka da ne postoji element reda 33 pada, pa je grupa ciklična. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|