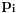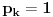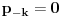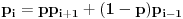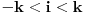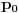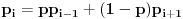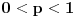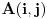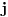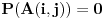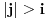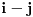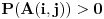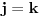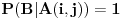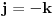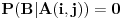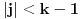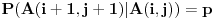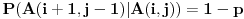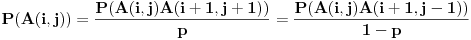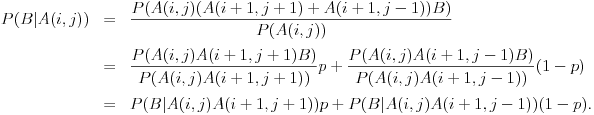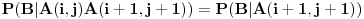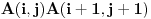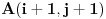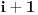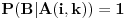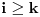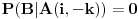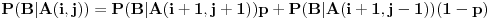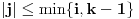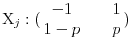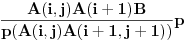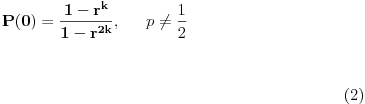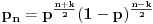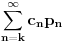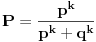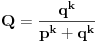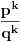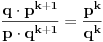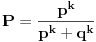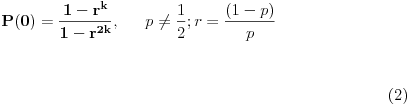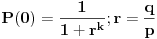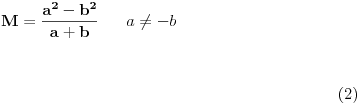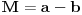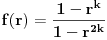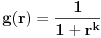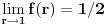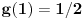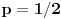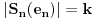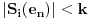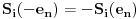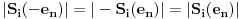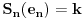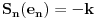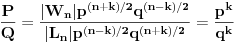|
|
[ beyn @ 19.01.2012. 15:21 ] @
|
| Pozdrav svima.
Potrebna mi je mala pomoc oko racunanja verovatnoce. Naime problem je sledeci:
Igrac A gadja u metu (igru pocinje sa 0 poena) . Za pogodak dobija +1 poen a za promasaj -1 poen. Igrac je pobedio ukoliko osvoji k poena a partija je izgubljena ukoliko osvoji -k poena.
Znajuci verovatnocu pogotka p i broj poena koji treba da se osvoji k odrediti verovatnocu da ce igrac A da pobedi.
Ja sam ovaj problem resio preko programcica koji sam napravio. Jenostavno se unosi verovatnoca pogotka i broj poena koji treba osvojiti, zatim se simulira 10000 igara i krajnja verovatnoca se dobija kao broj_pobedjenih_igara\10000 i to fino radi,
Sada imam zadatak da izracunam istu tu verovatnocu teorijskim putem (konkretno, mozemo da predpostavimo da je verovatnoca pogotka 0.2 i da treba osvojiti 3 poena za pobedu).
Da li neko ima ideju kako bi to moglo da se uradi?
|
[ kandorus @ 19.01.2012. 19:25 ] @
Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk
H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena
p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1
[ Nedeljko @ 19.01.2012. 20:51 ] @
Citat: kandorus: Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk
H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena
p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1
Hihihi! Probaj da rešiš tako kako si napisao za neki konkretan slučaj, recimo p=2/3, k=2.
@beyn
Neka je 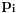 verovatnoća da će igrač pobediti ako trenutno ima  bodova.
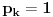 , 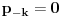 ,
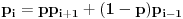 za 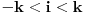 .
Kada rešiš ovaj sistem jednačina, 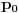 je vrednost koja te zanima. [ beyn @ 19.01.2012. 21:38 ] @
@Nedeljko
Hvala na odgovoru.
Samo jos jedno pitanje. Da li postoji neka teorema na kojoj se bazira to sto si naveo (ako postoji samo navedi ime zato sto cu je lako naci) tj. iz cega si to dobio ili si do resenja dosao cistom logikom ?
[ darkosos @ 19.01.2012. 22:25 ] @
Da ne treba slucajno 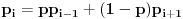 ? Ako je p verovatnoca da pogodi? [ kandorus @ 19.01.2012. 23:12 ] @
@Hihihi!
U čemu je problem? Ja sam samo izračunao verovatnoću da strelac sakupi k poena. Slično važi i za -k poena:
p(-k) = p^k/(1-p)^k, 1/2 < p <= 1
p(-k) = 1, 0 <= p <= 1/2
Za k=2 i p=2/3 dobije se da sa verovatnoćom 1 (sigurno) strelac osvaja 2 poena ali ne tvrdim da će da pobedi.
Kad smo već kod računanja. Za k=0 i p=0.5, koliko je pk po tvojoj računici?
[ beyn @ 19.01.2012. 23:14 ] @
@Darkosos
Meni deluje logicno ono sto je Nedeljko napisao, zato sto uvek iz i-te situacije u kojoj se nalazimo (-k<i<k) mozemo da idemo napred za jedan (u stanje i+1) sa verovatnocom pogotka (ako postignemo pogodak) i nazad za jedan (u stanje i-1) sa verovatnocom promasaja.
[ darkosos @ 19.01.2012. 23:20 ] @
Nemam pojma, mozda, ja sam to shavtio kao dolazak u situaciju i :) ili preko i+1 sa promasajem ili preko i-1 sa pogotkom...
[ Nedeljko @ 20.01.2012. 02:17 ] @
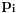 je verovatnoća da pobediš ako si trenutno u poziciji  . Treba samo čitati.
Radi se naravno o uslovnoj verovatnoći.
Pretpostavimo da je 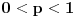 (preostali slučajevi su trivijalni). Neka je 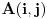 događaj da je igrač u  -tom gađanju imao 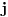 poena i  događaj da je pobedio. U tom slučaju je je 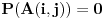 ako i samo ako je 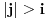 ili je 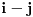 neparan broj. U suprotnom je 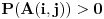 . Ovo mi treba zato što se uslovna verovatnoća može računati samo po uslovu čija je verovatnoća različita od nule.
Pretpostavimo da je  i da je 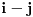 paran broj.
Ako je 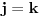 , onda je 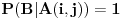 .
Ako je 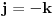 , onda je 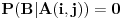 .
Ako je 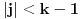 , onda je 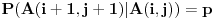 i 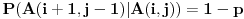 , odnosno 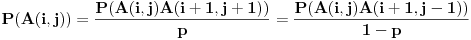 i pritom je
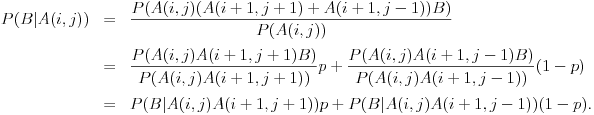
Tebi ostavljam da dokažeš da je u ovom slučaju 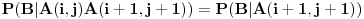 . Skup elementarnih ishoda je skup konačnih nizova nula i jedinica (pogotci i promašaji) takav da... Razmotri događaje 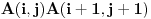 i 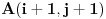 , tj. odnos skupova početaka nizova do pozicije 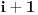 i završnih delova nizova, odgovarajuće verovatnoće itd. Na kraju vidi šta se krati i to je to.
U dobijenom sistemu jednačina
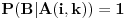 kada je 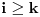 i  iste parnost kao  ,
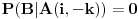 kada je 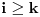 i  iste parnost kao  ,
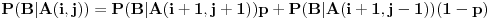 kada je 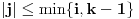 i  iste parnost kao 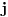 ,
možeš ignorisati  , a ti vidi zašto (imaš beskonačno mnogo nezavisnih sistema sa istim rešenjem).
[Ovu poruku je menjao Nedeljko dana 20.01.2012. u 15:40 GMT+1][ kandorus @ 20.01.2012. 02:55 ] @
U ovom zadatku ne važi da je
Citat: Skup elementarnih ishoda je skup konačnih nizova nula i jedinica (pogotci i promašaji)
već važi:
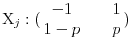
jer je slučajna veličina vezana za vrednost poena (+1 ili -1). [ darkosos @ 20.01.2012. 10:44 ] @
Ja se izvinjavam, ovo je postalo previse komplikovano za mene :)
[ beyn @ 20.01.2012. 11:26 ] @
Veliko hvala Nedeljko. Stvar je sada razjasnjena.
[ kandorus @ 20.01.2012. 12:50 ] @
Pa lepo, da li bi hteo i nama da razjasniš? Baš smo radoznali.
Meni je ovo Nedeljkovo "rešenje" zanimljivo i zato jer (množi i) deli dogadjaje i verovatnoće. Na primer jedan od članova u tim sabircima je
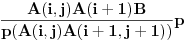
Neki bi rekli "deli babe i žabe". E sad to je moguće jer je tada rezultat oblika "a baba po b žaba". Problem je što se u Nedeljkovom rezultatu dobije verovatnoća. Obaška što A(r) nije definisano. Ali dobro šta se ja razumem.
[Ovu poruku je menjao kandorus dana 20.01.2012. u 14:46 GMT+1][ Nedeljko @ 20.01.2012. 14:47 ] @
Ispravljene su uočene greške u kucanju. No, rešenje je očigledno i ranije bilo jasno onome kome vredi objašnjavati, a zaista ne mogu da objašnjavam onima koji mogu da napišu ovako nešto
Citat: kandorus: Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk
H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena
p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1
ili
Citat: kandorus: @Hihihi!
U čemu je problem? Ja sam samo izračunao verovatnoću da strelac sakupi k poena. Slično važi i za -k poena:
p(-k) = p^k/(1-p)^k, 1/2 < p <= 1
p(-k) = 1, 0 <= p <= 1/2
Za k=2 i p=2/3 dobije se da sa verovatnoćom 1 (sigurno) strelac osvaja 2 poena ali ne tvrdim da će da pobedi.
Kad smo već kod računanja. Za k=0 i p=0.5, koliko je pk po tvojoj računici?
ili
Citat: kandorus: U ovom zadatku ne važi da je
Citat: Skup elementarnih ishoda je skup konačnih nizova nula i jedinica (pogotci i promašaji)
već važi:
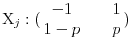
jer je slučajna veličina vezana za vrednost poena (+1 ili -1).
Ako darkosos bude tražio konkretnija pojašnjenja, potrudiću se, a oko tebe kandorus jednostavno nema svrhe truditi se. [ kandorus @ 20.01.2012. 16:36 ] @
Slučajna promenljiva iz postavke zadatka nije indikator dogadjaja (a što je ti predstavljaš navodeći da su u pitanju nizovi nula i jedinica). Ovde slučajna promenljiva uzima vrednost iz skupa {-1, 1}. Za indikator dogadjaja važi E(I) = p. Medjutim za slučajnu promenljivu koja uzima vrednost iz skupa {-1, 1} sa verovatnoćom {1-p, p} važi
E(X) = -1(1-p) + 1p = 2p - 1
Jasno je da te dve slučajne veličine nemaju istu raspodelu. Kako možeš dobiti tačno rešenje ako ti verovatnosni model nije korektan?
[ kandorus @ 21.01.2012. 12:21 ] @
Ovo što je Nedeljko izračunao u poslednjoj formuli se svodi na isto ono što sam ja dao za B1. Medjutim, kao što sam već napomenuo, primena te formula ne daje konačan odgovor na zadatak jer ne uzima u obzir mogućnost sakupljanja -k poena kada je partija izgubljena.
[ Nedeljko @ 21.01.2012. 14:44 ] @
kandorusu nemam nameru da odgovaram. Ovde pišem samo zbog onih koje bi on mogao da dovede u zabunu. Ako rešenje nije jasno onome kome treba da bude jasno, molim da mi to napiše, da se ne bih raspravljao sa kandorusom.
[ kandorus @ 21.01.2012. 15:29 ] @
Ne radi se niokom ponaosob već o rešenju. Ti osporavaš ono što sam napisao a sam dolaziš do iste formule. Medjutim ta formula nije potpun odgovor na zadatak. Osim toga ostaje otvoreno pitanje tipa promenljive. Ti polaziš od pretpostavke da je reč o promenljivoj tipa indikator dogadjaja. Ali takva pretpostavka nikako ne stoji. Bar je to očigledno jer indikator dogadjana ne može da ima negativnu vrednost a slučajna promenljiva iz ovog zadatka može. Matematičko očekivanje nije isto, disperzija (4p(1-p)) nije ista, ma to nisu promenljive sa istom raspodelom.
A osim toga, upravo zahvaljujući mojim primedbama ispravio si neke greške u tvom rešenju.
[ kandorus @ 22.01.2012. 01:43 ] @
Po uslovu zadatka je
P(-k) = 0, P(k) = 1
Prelazak iz stanja sa (-k+2) pogodaka u stanje sa (-k+1) pogodataka ostvaruje se sa verovatnoćom (1-p) pa je
P(-k+1) = P(-k+2)(1-p)
Ako je stanje sa (k-1) pogodaka tada sledećim hicem pobedjuje sa verovatnoćom p ili se prelazi u stanje (k-2) sa verovatnoćom (1-p). Zato je
P(k-1) = p + (1-p)P(k-2)
Za -k+1 < j < k-1 važi
P(j) = pP(j+1) + (1-p)P(j-1)
(p + (1-p))P(j) = pP(j+1) + (1-p)P(j-1)
pP(j) + (1-p)P(j) = pP(j+1) + (1-p)P(j-1)
p( P(j) - P(j+1) ) = (1-p)( P(j-1) - P(j) )
P(j) - P(j+1) = ( P(j-1) - P(j) )(1-p)/p
Ako se označi r = (1-p)/p dobije se
P(-k+2) = P(-k+1)(1+r)
P(-k+3) = P(-k+1)(1+r+r²)
...
P(j) = P(-k+1)(1+r+r² + ... + r j+k-1) (*)
P(j) = P(-k+1)(1 - r j+k)/(1 - r) (**)
r mora biti različit od 1 (u suprotnom je p=1/2).
Za j = k dobije se:
P(k) = P(-k+1)(1 - r 2k)/(1 - r)
1 = P(k) = P(-k+1)(1 - r 2k)/(1 - r)
P(-k+1) = (1 - r)/(1 - r 2k)
Koristeći dobijeni izraz za P(-k+1) i na osnovu (**) verovatnoća pobede je:
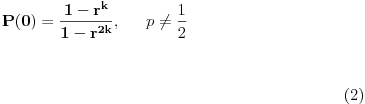
(*) Ako je p = 1/2 tada 1+r+r² + ... + r j+k-1 = j+k, pa je P(-k+1) = 1 / 2k
P(0) = k/2k = 1/2 [ Nedeljko @ 22.01.2012. 03:16 ] @
Ovaj put ti je rešenje dobro jer si prepisao uslove iz moje prve poruke i njih rešio.
Citat: kandorus: P(-k) = 0, P(k) = 1
P(j) = pP(j+1) + (1-p)P(j-1)
No, uporedi ovo sa svojom prvom porukom
Citat: kandorus: Bk - dogadjaj sakupljeno je (+)k poena
pk - verovatnoća dogadjaja Bk
H1 - dogadjaj da je prvim hicem meta pogodjena
H2 - dogadjaj da je prvim hicem meta promašena
p1 = p(B1) = p(H1)p(B1|H1) + p(H2)p(B1|H2)
...
pk = p^k/(1-p)^k, 0 <= p <= 1/2
pk = 1, 1/2 < p <= 1 [ darkosos @ 22.01.2012. 11:03 ] @
Pa, ja sam odustao jer mi se cini sve to previse komplikovano :) Probao sam da resim na neki drugi nacin, ali sam se zaglavio a nemam previse vremena da se bavim time.
Zadatak izgleda uopste nije naivan; ideja mi je bila da posmatram skupove pobeda u klasama duzine n; hocu reci, klasa bi bila skup svih pobeda u n >=k koraka.
Tu se lako vidi da je broj pogodaka (n+k)/2 a promasaja (n-k)/2; takvi skupovi pobeda su disjunktni pa bi se verovatnoca sabirala.
Verovatnoca svake pobede u n pokusaja je 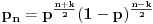 Problem je nastao kada sam pokusao da odredim koliko ima elemenata takva klasa, tj. na koliko nacina se moze pobediti u n koraka. Ako bih to nasao, npr neko c n, onda bi valjda ukupna verovatnoca biila 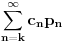 . A kako nisam uradio ni ovaj prvi deo, nemam pojma sta bi me sacekalo sa ovim redom :)
U svakom slucaju, posto to nisam uspeo da isteram do kraja, mogu samo da se slozim sa Nedeljkom za koga sam siguran da se dovoljno potrudio oko analize zadatka. [ kandorus @ 22.01.2012. 11:16 ] @
@Nedeljko
Pravo da ti kažem tu poruku nisam ni čitao do kraja zbog onog "Hihihi!". Posebno kad si kasnije uveo "indikator". A i da sam "prepisao" početne uslove trebalo je izračunati verovatnoću bez pretpostavke o "indikatoru" jer bilo bi neoprezno od mene da prepisujem nešto što sam osporio.
To jedno, a drugo, koristio sam formulu za verovatnoću pogotka prvim hicem, koju sam upravo ja prvi napisao. Ta formula stoji. Naravno, ja mogu sad da spekulišem da si ti prepisao od mene.
A što se tiče verovatnoće dogadjaja da je sakupljeno k poena te formule i dalje stoje. Još jednom, kao šro sam ranije napisao, to nije verovatnoća pobede. No ako ti misliš da je formula za izračunavanje "verovatnoće dogadjaja da je sakupljeno k poena" nije tačna niko ti ne brani da je izračunaš.
Ti i dalje braniš nešto što je neodbranjivo (pretpostavka o indikatoru) i da bi to maskirao napadaš nešto što niko ne brani. Jeste, napisao sam to što sam napisao i ja to ne sporim. Ono što sporim je kontekst koji si ti izvrnuo i sad ponavljaš "ko švaba tralalala" da sam nešto napisao. Da sam ćutao (kao što ti ćutiš o indikatoru) imao bi osnova da ponovo citiraš poruku. Pa objasnio sam u kom kontekstu sam napisao i nemoj se više truditi da promeniš kontekst (stalnim zvocanjem) već olovku u šake i izračunaj da li je tačno to što sam izračunao (ali u onom kontekstu kako sam napisao a ne tvoje zamene konteksta).
[ Nedeljko @ 22.01.2012. 16:03 ] @
darkosos
Ako ti ne ide na taj način, zašto ne probaš na drugi? Reci šta ti konkretno nije jasno u mom rešenju, pa ću pokušati da ti objasnim.
[ darkosos @ 23.01.2012. 07:39 ] @
Hvala ti Nedeljko, ali mene pre svega interesuje otkud ti ideja da na takav nacin resavas? :)
MIslim, nije bas tako ocigledno, ici preko uslovne verovatnoce za pobedu ako imas i poena... Mozda je to neka klasa problema u koju ovo upada?
[ Nedeljko @ 23.01.2012. 13:11 ] @
Pa, bio je neki sličan, ali ne isti zadatak sa pijancem koji stoji na litici i samo što ne padne, pašće ako napravi samo jedan korak napred (odmah), a pravi nasumične korake napred i nazad iste dužine. Takođe, ovaj zadatak se za k=2 svodi na to koji će teniser da osvoji gem pri rezultatu 40:40, o čemu sam već razmišljao.
[ kandorus @ 23.01.2012. 14:02 ] @
Rekao bih da su u pitanju lanci Markova.
[ Nedeljko @ 23.01.2012. 15:35 ] @
Jesu lanci Markova, ali to treba dokazati. Dao sam ideju kako.
[ darkosos @ 24.01.2012. 12:46 ] @
[ zzzz @ 24.01.2012. 16:09 ] @
Ovaj zadatak je sasvim jednostavan i može se odmah intuitivno riješiti.
Vjerovatnost pobjede P je:
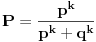 ,a poraza Q je: 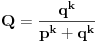 ,( p je šansa pogotka, q je šansa promašaja (p+q=1),a k je zadana razlika između broja pogodaka i promašaja.)
Dokaz intuitivnog rješenja:
Ako pođemo od tvrdnje da će razlika (kad tad) između pogodaka i promašaja biti k,(a ima dokaz za to!),onda slijedi:
-Ako se to desilo u k-tom pokušaju (a ranije nije ni moglo),onda je omjer između mogućnosti da je tada pobjedio ili izgubio jednak:
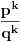 ,a šansa da je u takvom slučaju to baš bila P je : 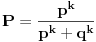
-Ako se to desilo u k+2-tom pokušaju ,onda je omjer između mogućnosti da je tada pobjedio ili izgubio jednak:
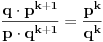 ,a šansa da je pobjedio je: 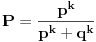
-Itd za svako k+2i (ako se desila razlika k) imamo isti omjer šansi .Pa ako će se to desiti u ko zna kom potezu šansa je ostala ista .
(Formula koju je napisao kanduros je ispravna samo nesređena,i izvedena na komplikovan način koji mi obični ne razumijemo.)
[ Nedeljko @ 24.01.2012. 18:41 ] @
Bravo zzzz!
[ kandorus @ 24.01.2012. 23:14 ] @
Citat: Formula koju je napisao kanduros je ispravna samo nesređena,i izvedena na komplikovan način koji mi obični ne razumijemo.
A ja se "satra" da ispišem što jednostavnije da svi ukapiraju.
[Ovu poruku je menjao kandorus dana 25.01.2012. u 10:16 GMT+1][ darkosos @ 25.01.2012. 07:39 ] @
Sjajno zzzz, i mene je bolela glava :) Jos samo treba dodati, da zbog toga sto trazis razliku k, mora biti P+Q=1, odakle verovatno i izvodis formulu za P (imas P/Q i P+Q, pa kao sistem jednacina). Ja sam se tu malo zabunio, pa zato kazem...
[ zzzz @ 25.01.2012. 21:51 ] @
Citat: kandorus: A ja se "satra" da ispišem što jednostavnije da svi ukapiraju.
Mislio sam na:
@kandorus:verovatnoća pobede je:
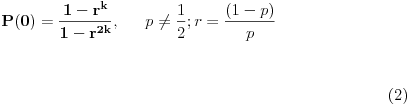 ,a moglo je ići kraćenje sa (1-r k) Pa bi bilo:
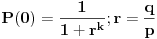 , izbjegao bi dodatno "satiranje" za p=1/2 koje nije lako ukapirati.Ne ljutiš se valjda?
Citat: Sjajno zzzz, i mene je bolela glava :) Jos samo treba dodati, da zbog toga sto trazis razliku k, mora biti P+Q=1, odakle verovatno i izvodis formulu za P (imas P/Q i P+Q, pa kao sistem jednacina).
Ja sam krenuo obrnuto.Ovako:Ako saznam da je strijelac završio gađanje,a ne znam kako je prošao,na šta bih se kladio?Pobjeda ili poraz?Kolika bi mi šansa bila da pogodim?I da li je važno znati u kom hicu se to desilo?Odgovore na ova pitanja lako je naći bez olovke i papira uz pivo u bučnoj kafani.Hvala vam na priznanjima,mada mislim da nema nekog razloga jer se ipak radi o jednostavnom problemu.
[ kandorus @ 25.01.2012. 22:38 ] @
Upppssss, za p=1/2 važi
1 - rk = 1 - ((1-p)/p)k =
= 1 - 1k = 0
a deljenje nulom nije dozvoljeno.
[ zzzz @ 26.01.2012. 08:00 ] @
Izvini ne razumijem šta želiš reći.Možeš li nama običnim koji to ne razumijemo malo razjasniti?
Da li bi po tvom išlo naprimjer ovako:
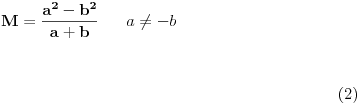 ,zbog a+b=0,"a deljenje nulom nije dozvoljeno."
A nipošto ovako:
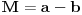 [ kandorus @ 26.01.2012. 09:25 ] @
Za izraz P/Q u svim tačkama za koje izraz Q uzima vrednost nula nije dozvoljeno delenje. U ostalim tačkama je dozvoljeno pa za taj izraz M upravo tako se i piše, M = a - b, a <> b.
Kad je u pitanju odredjivanje izraza za verovatnoću, u navedenom zadatku, samo je u mom rešenju razmotren slučaj p = 1/2. Rešenje bi bilo nepotpuno ako se taj slučaj ne razmotri jer bi tada došlo do delenja nulom kao što sam već objasnio,
E sad, ako ti i dalje nije jasno onda ne znam šta da kažem osim da zaključim da su moja objašnjenja iskomlikovana pa ne umem da prenesem ono što mislim. Čak ni Nedeljku nije jasno šta ja pišem te mi ponekad pripisuje da sam napisao ono što on misli a ne ono što piše. Kad njemu nije jasno kako će onda biti drugima? Pa ne znam, ne umem da budem jednostavniji (iako se "satra").
[ darkosos @ 26.01.2012. 09:35 ] @
Funkcije 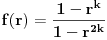 i 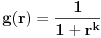 imaju razlicite domene;
ali posto je 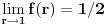 a 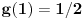 , kada bi dodefinisali f za r=1, tako da je f(1)=1/2, takve dve funkcije jesu identicne, jer imaju isti domen i svuda jednake vrednosti.
Ovo sve posmatrano za r>=0. [ Nedeljko @ 26.01.2012. 10:33 ] @
kandorus je u pravu da bi u njegovo rešenje bilo nepotpuno bez posebnog razmatranja slučaja 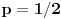 jer je njegov postupak takav da bi se u tom računu pojavilo deljenje nulom. [ darkosos @ 01.02.2012. 08:03 ] @
E, ja moram da dodam jos nesto :)
Rekao bih da verovatnoca da igrac dobije u k+2 poteza nije p k+1q, vec "broj varijanti pobeda u k+2 poteza" * p k+1q.
Srecom, sve ostaje isto, zato sto je i "broj varijanti poraza u k+2 poteza" isti broj kao onaj gore.
Ne mogu da izdrzim a da to ne pokazem :)
Dakle, ako je npr Wn skup pobeda u n koraka a Ln skup poraza u n koraka, treba pokazati da je |Wn|=|Ln|. Ovo moze da se izvede koristeci funkciju f(en) = -en koja urejdenu n-torku iz {-1,1} n slika u isti taj skup tako da pomnozi svaku koordinatu sa -1, tj. pretvori promasaj u pogodak i obrnuto. Pokazacu da na taj nacin f slika pobedu u poraz i obrnuto (sjajna stvar :).
Da bih prikazao osobine elementarnog dogadjaja, uvescu sumu Si(en) koja predstavlja sumu koordinata, tj. bodova prvih i elemenata uredjene n-torke en. Da bi en bio elementarni dogadjaj ove igre, mora biti
1. 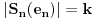
2. 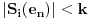 za i=1,..,n-1
Lako se vidi da je 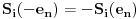 pa je 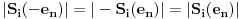 za i=1,..,n odakle se vidi da i -e n zadovoljava prethodna dva uslova.
Takodje, posto 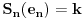 znaci pobedu, a 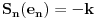 poraz, ova funkcija zaista preslikava pobedu u poraz i obrnuto.
Ostaje da se pokaze jos da je f:Wn->Ln bijekcija. 1-1 jeste sigurno jer je to na {-1,1} n. Iz tog razloga je i |Wn| = |f(Wn)|. Posto je f(Wn) podskup Ln i f(Ln) podskup Wn, vazi:
 . Pocetak i kraj su jednaki pa su i ovi u sredini.
Konacno,
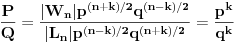 [Ovu poruku je menjao darkosos dana 01.02.2012. u 09:23 GMT+1]
[Ovu poruku je menjao darkosos dana 01.02.2012. u 09:30 GMT+1]
[Ovu poruku je menjao darkosos dana 01.02.2012. u 09:23 GMT+1]
[Ovu poruku je menjao darkosos dana 01.02.2012. u 09:30 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|