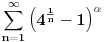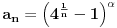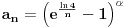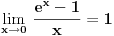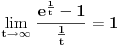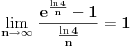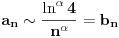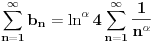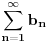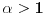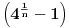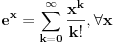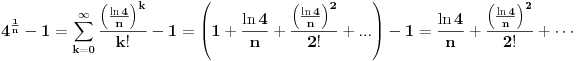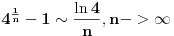[ salchin @ 24.01.2012. 15:12 ] @
[ SrdjanR271 @ 24.01.2012. 17:41 ] @
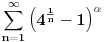
Opšti član reda je
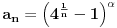
.
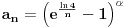
.
Iskoristimo sad poznat limes
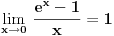
.
Smena x=1/t.
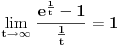
.
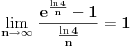
Znači imamo
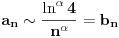
, kad
.
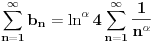
.
Na osnovu konvergencije hiperharmonijskog reda
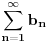
konvergira za
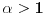
.
Na osnovu drugog poredbenog kriterijuma
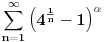
KV za
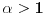
.
[ SrdjanR271 @ 24.01.2012. 17:50 ] @
Drugi način.
Razvijamo
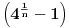
u red na osnovu reda
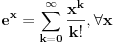
.
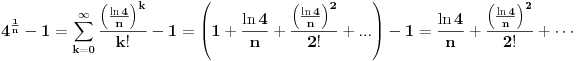
Odavde zaključujemo
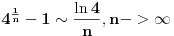
.
Dalje sve isto kao u prethodnom postu.
[ salchin @ 24.01.2012. 18:16 ] @
hvala druze, punoo ti hvala...
nemas predstave koliko sam ti zahvalan :)
jos jedno pitanje...
da nema neko kakvu zbirku PDF formata u kojoj imaju rijeseni zadaci sa redovima...
ovo mi je najkomplikovaniji dio analize, pa zato pitam...
hvala jos jednom...
[ SrdjanR271 @ 24.01.2012. 18:24 ] @
Kucaj na guglu. Ima toga po netu.
Na engleskom series, infinite series....
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.