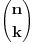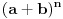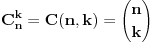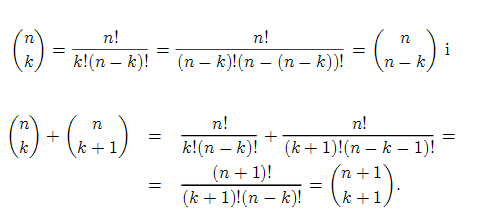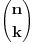
Ne razumem, ako nema onda to nije binomna forumula i to nije jednako
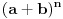
Inace, binomna formula se dokazuje preko indukcije (moze i drugacije, preko kombinatorike na primer).

Evo sad vidim u zadatak ima n i k samo pise na istom mjesu C pa gore k a dolje n. To je to valjda.
Nasao sam nesto pa mi recite da li je tako...
(a+b)^1 =(1 a ispod jedinice 0) a + (1 i ispod jedinice 1) b = a+b

eto ako ste me dobro shvatili ovo 1 a ispod jedinice 0 je ono u veliku zagradu isto kao to n i k :D
ZNaci ovako pocinje pa oonda imaju jos 3 formule iste samo ide (a+b)^2...(a+b)^4
Da li je ovo taj dokaz?

Evo ovako

Znaci ovo je taj dokaz. Ovo mi je za ispit. Mogu li sam ovu sliku u sredinu da kopiram?

Postavio sam slicnu temu prije nesto malo manje od godinu dana,pogledaj sta mi je Nedeljko odgovorio: http://www.elitesecurity.org/.

Nijesi poslao pravi link... Ljudi recite mi da li je to to one 3 slike da napisem kao odgovor? Valjda ona prva slika ne treba jel?
Neka potvrdi neko pa da polozim to sjutra :)))

Ova prva ti je da bi ti razumeo sta su binomni koeficijenti.
A tvoj trazeni dokaz su ti 2 i 3 slika.

Uh smorih vise pogotovo soneca :D
Evo jos jedno pitanje:
Dokazati formule: C gore k dolje n= C na n-k a dolje n i C gore k dolje n= C gore k-1 dolje n-1 + C gore k dolje n-1

Eto to isto ima dobrro ovo napisah :D

Prvo, zbog notacije:

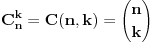
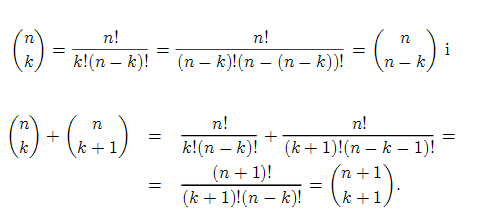
Primeti da je ovo drugo svojstvo korisceno u dokazu binomne formule, kod uglastih zagrada (pogledaj dokaz).

Brate evo ovo nam je dao profesor. Mozes li mi reci da li je ovo odgovor na ova 2 pitanja? Cisto jer je krace pa zato bi dobro bilo ako jeste :D
Evo link za pdf fajl pogledaj na 14 stranici tu ti je to. http://www.mediafire.com/?i3cwbt02wb10wa6

Sedi i uči umesto da tražiš načine kako da se provučeš. Ako nisi sposoban da sam zaključiš ni šta je definicija, šta formulacija teoreme, šta dokaz teoreme — očigledno je jedino smisleno da padneš ispit pa da za sledeći put naučiš kako treba.