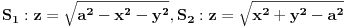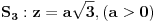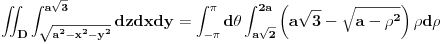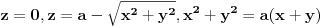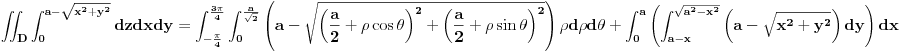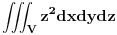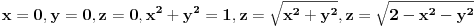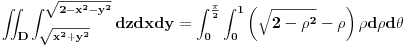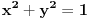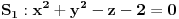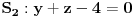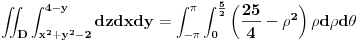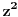[ Sonec @ 24.01.2012. 17:50 ] @
|
| Vezbam zadatke sa rokova, a nemam resenje, pa bi valjalo da proverim dal mi ista valja. Samo da li sam dobro odredio integrale, racun mi nije vazan.
1.Izracunati zapreminu tela ogranicenog povrsima 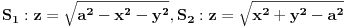 i i 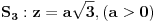 . .
Moje resenje: 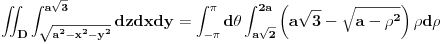
2.Naci zapreminu tela koje je ograniceno povrsima 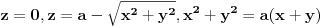 gde je gde je  . .
Moje resenje: 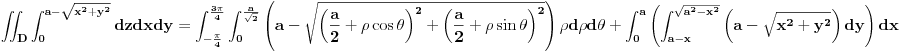
E sad, ovaj prvi integral nema bas "lepu" potkorenu velicinu, i pitanje je kako njega uraditi. Ovde sam koristio pomerene polarne koordinate. Mozda se zadatak lakse radi sa standardnim, to cu proveriti kasnije.
3.Izracunati integral 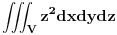 , gde je , gde je  skup u skup u 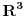 ogranicen povrsima ogranicen povrsima 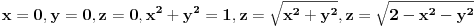 . .
Moje resenje: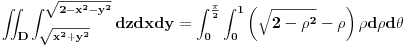
I da, jos jedno pitanje, da li nam ovaj uslov 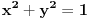 uopste treba? uopste treba?
4.Izracunati zapreminu tela ogranicenog povrsinama 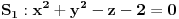 i i 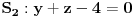 . .
Moje resenje: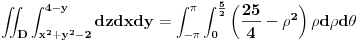
[mimo ovoga, da li moze nekako ovo D npr. da se napise ispod integrala?]
[Ovu poruku je menjao Sonec dana 24.01.2012. u 19:03 GMT+1] |
[ SrdjanR271 @ 24.01.2012. 18:12 ] @
Ja sam prvo gledao treći.
Taj uslov x^2+y^2=1 je tu samo da zbuni izgleda.
Kolko vidim da si ti radio kao da se radi o prvom oktantu. Meni nije jasno ni zašto su dati uslovi x=0,y=0,z=0.
Gde ti se izgubilo z^2 iz početnog integrala?
[ Sonec @ 24.01.2012. 18:23 ] @
Zaboravio sam na
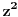

[ Sonec @ 25.01.2012. 21:42 ] @
Ovo resenje prvog zadatka nije dobro, to sam primetio danas, fali jos jedan deo, ako to nekoga uopste zanima...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.