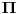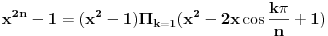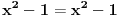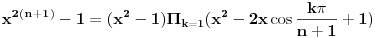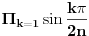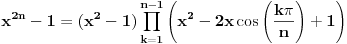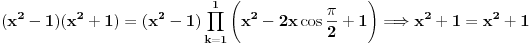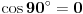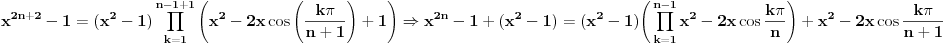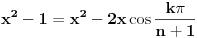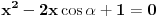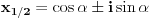[ Rato iks de @ 24.01.2012. 21:10 ] @
|
[ edisnp @ 24.01.2012. 21:46 ] @
[ Rato iks de @ 25.01.2012. 16:06 ] @
Misliš da sada ovaj zadnji izraz treba provjeriti za savko n osim -1?
Imaju dvije nepoznate x i n. Nema ni nekog uslova ni nešto za ovu drugu relaciju. Uradim sledeće: 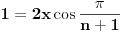 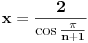 . Ne razumijem kako ovo da dokažem. . Ne razumijem kako ovo da dokažem.Ako možete samo provjeriti još da li je tačan ovaj zadatak. U pitanju je niz i ispitati da li je rastući i neogranićen. Hvala [ Nedeljko @ 25.01.2012. 16:25 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|