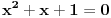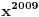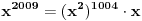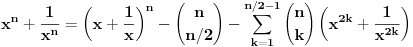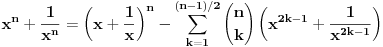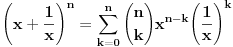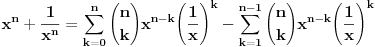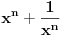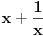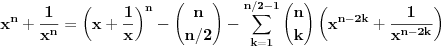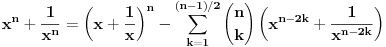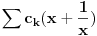[ miljakovic @ 26.01.2012. 18:20 ] @
| ako je x^2+x+1=0 odredi x^2009+1/x^2009. zadatak sa prijemnog na etf iz 2009. ja sam krenuo redom da racunam x^n+1/x^n i dobio da je uvek =-1 sem kad je stepen deljiv sa 3, onda je =2. pri cemu sam dobio da je x+1/x=-1 iz pocetnog uslova ima li neko resenje bez pesacenja, nego uz pomoc nekog rastavljanja? |