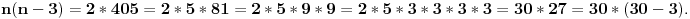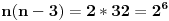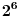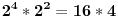[ zeljko.m @ 27.01.2012. 17:14 ] @
| Postovani, ne mogu da skontam kako resiti ovaj zadatak: Moze li broj dijagonala mnogougla da iznosi: a) 32 b) 118 c) 405? Znam da se broj dijagonala izracunava pomocu ove formule: D=n*(n-3)/2, ali ne znam kako na osnovu ove formule da izracunam cemu je jednako n? Unapred zahvaljujem. |