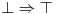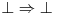[ vladadada @ 02.02.2012. 20:28 ] @
|
| Kod relacija imam svojstva relacije: refleksivnost, simetricnost, antisimetricnost i tranzitivnost (i funkciju ali to mi ne treba sada). Pitanje je: Koja svojstva ima prazan skup?
Tacnije, relacija je definisana ovako:
{(x,y) | x+y=0, x,y pripadaju N}
sto bi trebalo da bude prazan skup
Dvoumim se izmedju:
1) simetricnost, antisimetricnost i tranzitivnost (nije refleksivan jer je zadatak u skupu prirodnih brojeva)
2) nista od navedenog
Hvala unapred! :) |
[ darkosos @ 03.02.2012. 07:31 ] @
Hm, pa nesto nisam siguran da ima smisla ispitivati praznu relaciju. I generalno, osobine elemenata praznog skupa. Mislim, sve osobine ti podrazumevaju da su neki x i y u relaciji, pa posto nema takvih mozes da kazes sta hoces.
Na primer, da za sve
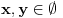
vazi da je x>y i y>x. Ili stagod ti padne na pamet...
Priseti se samo da
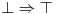
kao i
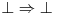
[ Nedeljko @ 03.02.2012. 12:55 ] @
Ima smisla i baš iz razloga koji si naveo je relacija tranzitivna, simetrična i antisimetrična. Naravno, ne može biti refleksivna osim ako je skup nnosač prazan, a to se valjda isključuje iz razmatranja. Puna i prazna relacija na nepraznom skupu se itekako razmatraju.
[ darkosos @ 03.02.2012. 13:10 ] @
Ako sam dobro razumeo, ove osobine su posledica upravo toga sto je relacija prazna? To znaci da ne zavisi od toga kako je zadana? Pa bi tako sve prazne relacije uvek imale iste osobine...
[ Bojan Basic @ 03.02.2012. 15:14 ] @
@darkosos:
Prazna relacija je jedinstvena za dati nosač.
[ darkosos @ 03.02.2012. 19:11 ] @
Hm, dobro, jedinstvena na nekom skupu, kakogod zadata. Ali, hocu da kazem, mogu li se osobine koje je Nedeljko pomenuo menjati u zavisnosti od nosaca?
Ili je bitno samo da li je prazan ili ne. Hocu reci, ako su date osobine izvedene samo iz cinjenice da je prazna, onda ni sam nosac nema znacaja u smislu koje ce osobine takva relacija imati.
[ Nedeljko @ 03.02.2012. 20:00 ] @
Navedene osobine u slučaju prazne relacije ne zavise od izbora nosača, a ako izabereš neku drugu osobinu, onda je to druga stvar. Recimo, da li postoji bar pet elemenata (nosača) koji nisu u relaciji sa samim sobom?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.