Postoje gornja i donja Darbuova suma: i , gde je podela intervala pri cemu se zahteva da je funkcija ogranicena.
Dok, pak, Rimanov zbir je gde je izbor istaknuth tacaka podele

Neke korisne osobine: ako je finija od ) tada je , zatim, ako su i u bilo kojem odnosu uvek vazi i mozda jos, za svaki izbor istaknutih tacaka vazi

Samo ispravi za , tada kazemo da je P₁ finija od P₂ i tada vaze nejednakosti i

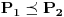
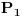
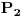
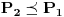
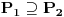
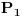
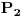
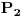
Moj profesor Analize je sa obelezavao cinjenicu da je podela finija od podele (a ne ), al bez obzira na to, ja sam u zagradi objasnio sta sam podrazumevao pod tim zapisom, i date nejednakosti tada i vaze, tako da nema potrebe da nista menjam. Ovaj zapis vise odgovara Rimanovom visestrukom integralu, dok kod Rimanogov integrala bi odgovarao zapis (podela je finija od podele , odnosno, podela je grublja od podele ). 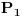Ako se negde uci da ova oznaka znaci suprotno, onda je to njihova stvar. Za mene je logicniji zapis kako sam ja stavio, al ako se nekome to ne svidja, on to moze da obelezi kako mu je volja.

Kod mene u knjizi Predavanja iz Analize 1 je oznaceno bas suprotno kao sto si napisao... probao sam da nadjem na internetu kako se oznacava finija podela, ali nasao sam samo definiciju sa relacijom ... Meni nije logicniji, ali u pravu si, ako si tako definisao onda nemoj nista da menjas! :)