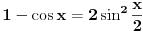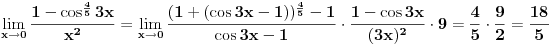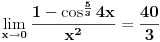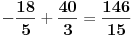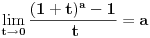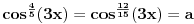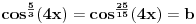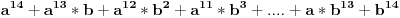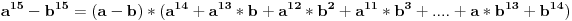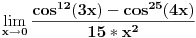|
|
[ duo18 @ 06.02.2012. 18:22 ] @
|
| lim 4koren iz cos na 3 *5x - 5koren iz cos na 4 *3x/x na 2
x→0
lim 1-(cos5x)na 3/4 - 1 + (cos3x) na 4/5 /x na 2
x→0
znam da treba da svedem na oblik 1-cosx/x na 2 ali do ovde stignem i ne znam sta dalje... moze li pomoc ? |
[ SrdjanR271 @ 06.02.2012. 19:16 ] @
[ SrdjanR271 @ 06.02.2012. 19:24 ] @
[ duo18 @ 06.02.2012. 22:10 ] @
[ duo18 @ 07.02.2012. 16:55 ] @
Hoce li neko da preoba da uradi ovaja zadatak? Bio bih mu zahvalan,jer ja dva dana vec pokuasvam da uradim ali ne ide...
[ miki069 @ 07.02.2012. 17:17 ] @
Jel sme Lopitalovo pravilo ili razvoj funkcije u Mekloranov polinom?
Ručno (svođenjem na tablični limes) je velika gužva.
[ duo18 @ 07.02.2012. 17:31 ] @
Samo svodjenje na tablicni limes.Da moze lopital ne bih se mnogo mucio oko ovog...
[ SrdjanR271 @ 07.02.2012. 20:07 ] @
Pogledaj u Veneovoj zbirci za 4-tu godinu zadatak broj 99.
[ miki069 @ 07.02.2012. 23:43 ] @
Srđanje u mojoj Venovoj zbirci za 4-tu godinu 99-ti zadatak je iz kombinatorike.
Izdanje mnogo matoro.
Ta Venova zbirka ima mnogo izdanja.
[Ovu poruku je menjao miki069 dana 08.02.2012. u 02:09 GMT+1]
[ SrdjanR271 @ 08.02.2012. 00:12 ] @
Ova je 32-o izdanje.
Uglavnom zadatak je iz limesa.
A pitanje za duo18: odakle je zadatak?
[ Sonec @ 08.02.2012. 00:33 ] @
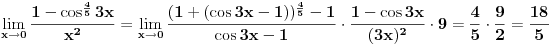
slicno dobijamo
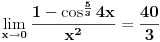
Konacno, 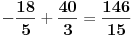
U prvom limesu treba minus svuda, al bilo mi lakse ovako da pisem  [ miki069 @ 08.02.2012. 01:00 ] @
Bravo Sonec.
Tabličan limes: 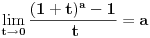 koji važi za a>0.
Ja se ubih da racionališem nešta što je praktično nemoguće racionalisati.
Teoretski moguće, kao 15-te korene, ali se onda ulazi u duboku šumu. [ miki069 @ 08.02.2012. 01:30 ] @
Metoda grube sile.
Radi jednostavnosti pisanja uvešćemo smene:
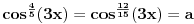 i
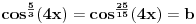
Proširimo razlomak sa 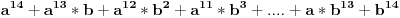
Korišćenjem jednakosti: 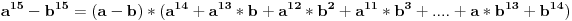
i osobina limesa, traženi limes postaje jednak:
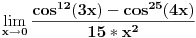
Dovedeni limes izgleda samo "lepše" od početnog, ali je iste težine.
Mislim da je jedini način da se reši, upravo način koji je Sonec izložio.
Mnogo dobar zadatak.
Što reče Srđan, Duo18, odakle ga bre iskopa???
[Ovu poruku je menjao miki069 dana 08.02.2012. u 03:04 GMT+1]
[Ovu poruku je menjao miki069 dana 08.02.2012. u 03:04 GMT+1][ duo18 @ 08.02.2012. 04:07 ] @
Zadatak je sa kolokvijuma na tehnoloskom fakultetu.I ja sam radio kao sto je miki069 ali ocigledno to je pogresan nacin... :)
Hvala sonec !
[ Bojan Basic @ 08.02.2012. 14:46 ] @
Citat: miki069:
Mnogo dobar zadatak.
Pošto je zadatak rešen, valjda je OK nastaviti temu u ovom smeru. 
Mislim da je ovaj zadatak izuzetno loš (i ne samo ovaj, gomila sličnih, često se pojavljuju i na ovom forumu). Zašto? Zato što smatram nedopustivim da postavka glasi „Izračunati limes taj-i-taj, bez upotrebe Lopitalovog pravila?“ Kada će neki inženjer (ili bilo ko kome treba računanje limesa u životu) doći u praktičnu situaciju da izračuna neki limes, ali da mu je pritom zabranjeno koriščenje ovog ili onog metoda?
Naravno, postoje pedagoški razlozi zbog kojih se na kolokvijumima daju i limesi koje treba rešiti bez primene Lopitalovog pravila. Ali, u tom slučaju smatram dužnošću onoga ko zadatke sastavlja da smisli zadatak koji se ne može rešiti primenom Lopitalovog pravila (ili, ako i može, da onda . Ovo što se radi (uzme se zadatak koji ima rešenje u dva reda primenom neke tehnike, pa se zahteva da se reši ali zabranjujući primenu te tehnike) prikazuje (po mom mišljenju) nesposobnost postavljača zadataka da pripremi odgovarajuće zadatke za kolokvijum. (Izvinjavam se ako je ova izjava previše teška, ali ipak u potpunosti stojim iza nje.)
I najzad, šta uopšte znači „...bez primene tog i tog metoda“. Evo, konkretno, da li je ovo što ću sad skicirati validno rešenje navedenog limesa, bez upotrebe Lopitalovog pravila?
Rešenje: Dokažimo prvo pomoćnu lemu.
Lema: (Ovde sad ide formulacija Lopitalovog pravila — naravno, bez pominjanja naziva „Lopitalovo pravilo“.)
Dokaz leme: (Naravno, ovde ide dokaz Lopitalovog pravila, opet bez ikakvog pominjanja imena.)
Rešenje limesa: (Sad ovde lepo rešim limes u dva reda, kako „lema“ dozvoljava.)
Kraaaaaj. Ako mi neko zameri da sam ipak koristio Lopitalovo pravilo — ne znam ja ništa ni o kakvom Lopitalovom pravilu, ja sam na licu mesta smislio lemu koja mi pomaže da rešim zadatak, dokazao je, i primenom te leme rešio zadatak. Lopitalovo pravilo, šta to beše?
Zapravo, paradoksalno je to što je vrlo moguće da bi ovakvo rešenje (dakle, sve sa ispisivanjem dokaza) stvarno oduzelo drastično manje vremena nego traženje predviđenog rešenja (poput onog Sonecovog). Dakle, student bi mogao jednom da nauči dokaz Lopitalovog pravila, kao pesmicu (što je najgrđe, ne mora čak ni da razume taj dokaz!), a onda sve slične „zadatke“ rešava kao iz rukava. No, to ipak ne preporučujem — uvek ostaje mogućnost da će pomenuti nesposobni sastavljač zadataka shvatiti da ga je student preveslao, pa zaključiti da ponuđeno rešenje ipak nije „rešenje bez upotrebe Lopitalovog pravila“, te ga oceniti sa zasluženih 0 bodova (mada je zapravo jedina „mana“ ovakvog rešenja to što ono nije bilo predviđeno).
Komentari su, naravno, dobrodošli. Mislim da se od ovog može razviti lepa diskusija — a duo18 se valjda neće ljutiti što mu okupiramo temu, pošto je zadatak svakako rešen.  [ berazorica @ 08.02.2012. 17:05 ] @
U više navrata sam (zlo)upotrebila ovaj Bojanov recept i - prošlo mi je! Npr. sastavljač zadatka predvidi korišćenje Banahove teoreme o fiksnoj tački, ali data osobina može se pokazati metodama iz analize 1. Ili, traži se da, poznavajući određeni program, pokažemo da za neke druge ulazne podatke zadatak nema rešenje, a moguće je logički pokazati da rešenje ne postoji i onda samo objasniti šta bi to značilo u programu...
Ipak, ako bismo podele na oblasti u matematici smatrali neprirodnim, gde je onda granica takvih mogućnosti? Šta bi Bojan rekao kad bi mu student na ispitu iz geometrije zadatak rešio metodama analitičke geometrije? Ili su zadaci baš tako pažljivo odabrani, da je to nemoguće?
[ Bojan Basic @ 08.02.2012. 18:39 ] @
Citat: berazorica:
Šta bi Bojan rekao kad bi mu student na ispitu iz geometrije zadatak rešio metodama analitičke geometrije? Ili su zadaci baš tako pažljivo odabrani, da je to nemoguće?
Prihvatio bih rešenje, naravno — štaviše, uz pohvalu studentu (uvek mi je drago kada neko reši zadatak drugačije nego što sam predvideo). A drugo je pitanje da li mi se to nekad desilo u praksi: nije (mada nešto donekle slično jeste, biće reči o tome pri kraju poruke). Kako to da se navedeni primer nikada nije desio? Zadaci nisu tako pažljivo odabrani da je rešenje putem analitičke geometrije nemoguće — u stvari, kada biram zadatke za kolokvijum, priznajem da i ne pomišljam na to koliko bi rešenje putem analitičke geometrije bilo komplikovano. No, ipak, analitička geometrija je malo specifična: iako se putem nje se može rešiti recimo 70% geometrijskih zadataka, verovatno je u 95% takvih primera rešenje neuporedivo složenije nego rešenje putem elementarne geometrije (procenti su odokativno navedeni, ali mislim da je suština jasna).  To može biti jedno objašnjenje kako to da još nisam dobio rešenje zadatka putem analitičke geometrije. No, bojim se da postoji i drugačije: nažalost, stičem utisak da je šablonizacija matematike u glavama studenata sve izraženija (za šta ne kažem da su sami odgovorni, bar ne sasvim — dobar deo krivice jeste na onima oni koji na šablonski način predaju raznorazne predmete, a da pritom sve to može i mnogo drugačije). Prosto, student maltene svaki predmet doživljava kao gomilu šablona koje treba da nabifla napamet, i kad ga jednom položi — e, onda mora da isprazni glavu od tih šablona, kako bi u nju stali šabloni za sledeći predmet. (Naravno, ni slučajno ne tvrdim da ovo važi za sve studente. Samo ističem pojavu koja deluje da sve više uzima maha.)
Baš mi u toku pisanja ove poruke pade na pamet jedan baš upečatljiv primer. Održavan je prijemni ispit za doktorske studije matematike, i bio je jedan geometrijski zadatak. Ispostavilo se da je taj geometrijski zadatak „dušu dao“ za rešavanje analitičkom metodom (naravno, postojalo je i vrlo pristojno elementarno rešenje, čak više različitih, ali se prosto uklopilo tako da i analitička geometrija rešava zadatak očas posla). Apsolutno svi koji su rešili zadatak rešili su ga elementarnim putem. I posle prijemnog razgovara jedna studentkinja koja nije prošla prijemni, ali joj je malo falilo, s jednim članom komisije za pregled zadataka s tog prijemnog. Ta studentkinja nije rešila pomenuti zadatak. Pomenuti profesor joj pokazuje razne načine za rešavanje, i dodaje: „A i ako ti nije palo na pamet ništa od ovoga, mogla si bar pokušati analitičkom geometrijom, evo vidi koliko se brzo stigne do rešenja“. Studentkinja, sva zatečena ovim poslednjim komentarom, dodaje: „A to je smelo da se radi??!!“ Dakle, naglašavam još jednom, u pitanju je prijemni za doktorske studije, pomenuta studetkinja je vrlo dobra (kasnije je i položila prijemni, u drugom krugu, i trenutno je na doktorskim studijama) — pa je sva šokirana saznanjem da se geometrijski zadatak sme rešavati i analitičkim putem!
No, svrh svega mislim da primer analitičke geometrije i nije baš u skladu s temom. Ovde je zadatak bio rešavanje limesa uz zabranu primene Lopitalovog pravila, a da je pri tome Lopitalovo pravilo rađeno iz istog predmeta, čak u istoj tematskoj celini (izračunavanje graničnih vrednosti), i zabranjeno je jedino iz razloga što vodi do rešenja u dva reda! Rekoh ranije: sigurno nije loša ideja proveriti na kolokvijumu ume li student da rešava limese na neki drugi način, a ne primenom Lopitalovog pravila. Ali onda mu lepo daj limes koji mora da rešava na drugi način — tako ćeš em postići šta si hteo (proveriti ume li se on snaći i bez Lopitalovog pravila), em će studentu biti jasno zašto on treba da zna i druge stvari pored Lopitalovog pravila (zato što postoje limesi za koje Lopitalovo pravilo nije bogomdano — dok se, nasuprot tome, u primeru iznetom u temi studentu maltene šalje poruka da Lopitalovo pravilo funkcioniše uvek, ali da za neke limese asistent/profesor prosto „’oće nešto drugo“?!). Pravi geometrijski pandam ovakvom primeru bio bi kada bih na ispitu zahtevao od studenata da reše neki zadatak, ali bez korišćenja Pitagorine teoreme. Duhovito.
Uglavnom, evo onog primera koji sam najavio na samom početku. Jednom prilikom zadao sam ovakav zadatak: bila je data kružnica 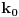 , nešto se u njoj dešavalo, i tu je trebalo nešto dokazati (nisu sad bitni detalji). Uglavnom, moja ideja je bila da se uoči sledeće: ukoliko kružnicu  zamislimo kao apsolutu Poenkareovog modela, svi drugi posmatrani objekti imaju svoju interpretaciju kao određeni hiperbolički pojmovi, i ispostavlja se da je postavka zadatka zapravo prepričavanje, u Poenkareovom modelu, određenog zadatka iz hiperbolične geometrije urađenog na vežbama. Kako Poenkareov model predstavlja model hiperbolične geometrije, sve što važi u hiperboličnoj geometriji važi i u njemu, te tvrđenje zadatka sledi iz tvrđenja dokazanog na vežbama. Ta konstatacija bila je sve što sam ja očekivao kao rešenje zadatka. Neki studenti su to i primetili, i dobili maksimalan broj bodova. No, jedna studentkinja to nije primetila, već je zadatak rešavala na potpuno euklidski način, i posle ispisane dobre tri strane zaista dokazala ono što se tražilo. Naravno, i ona je dobila maksimalan broj bodova, i još sam je jednom kasnijom prilikom pohvalio, uz napomenu da mi je veoma drago što je demonstrirala da se zadatak može rešiti i tako. Je li ona tu pokazala neko znanje iz hiperbolične geometrije (budući da je zadatak bio zamišljen da bude iz te oblasti)? Očigledno nije pokazala ni da zna da postoji hiperbolična geometrija, a kamoli kako ona izgleda (naravno, ja ne tvrdim da ona to ne zna, samo se prosto iz njenog rešenja ne može ama baš ništa reći o tome). Je li ona tu pokazala da ume razmišljati svojom glavom? Apsolutno jeste. Pritom, hiperboličnu geometriju će najverovatnije svakako brzo zaboraviti, a sposobnost matematičkog načina razmišljanja će imati doveka. Zato je ovo drugo i jedino što me zanima kod studenata. [ Sonec @ 08.02.2012. 19:04 ] @
Sve je to lepo, ali, ako bi neko zeleo da resi zadatak tako sto ce dati iskaz i dokaz Lopitalovog pravila (naravno, tom prilikom ne zvati ga tako) trebalo bi mu dosta vremena. Sam dokaz Lopitalovog pravila (u full paketu, e sad, ako se limes svodi na samo poseban slucaj onda naravno treba manje vremena) nije uopste lak, to je jedno celo ispitno pitanje iz Analize 1 (preciznije, Analiza 1a). Dokaz koji je meni poznat (i koji sam ja ucio) ima bar 2 pune strane A4 formata, pri cemu su se neke strane nejednakosti (i slicno) radile na dualan nacin, pa nisu navodjene. Dalje, pitanje je koliko bi studenata (ako bi htelo da uradi ovaj zadatak ovom metodom) znalo da da dokaz Lopitalovog pravila, ja sam siguran da bi to mozda znalo 5 do 7 ljudi na 200 studenata, jer ce 90% studenata poceti sa spremanjem usmenog tek posle pismenog, tako da nisu ni gledali dati dokaz.
I u ovom zadatku, da, tacno je, treba 2 reda primenom Lopitala, ali kakva, prvom prilikom kada se koristi Lopital ne dobije se tako rogobatan izraz, ali kada se na taj novonostali izraz primeni ponovo Lopital dobije se jedan poveliki izraz, za cije racunanje (tj. dolazenja do njega) treba dosta vremena. Ali, kao sto kazes, sve zavisi i od fakulteta do fakulteta, konkretno, ako je u pitanju matematicki fakultet i ako je receno da ne sme da se koristi Lopital onda tako treba i postupiti (tj. nema nikakvog navodjenja pomocnih dokaza Lopitala i slicno), jer, ako se na matematickom fakultetu ne uradi na taj nacin (bez Lopitala), a gde ce onda da se uradi? (da nece mozda na poljoprivrednom (bez ikakvog potcenjivanja fakulteta)).
Sto se tice same geometrije (posto smo/ste se dotakli i toga) na matematickom fakultetu u Beogradu je iz Geometrije 2 (geometrija poretka, euklidska, hiperbolicka) izricito receno i stavljeno do znanje da je zabranjena upotreba analiticke geometrije, trigonometrije i slicnih "metoda", i da takva resenja nece biti uzimana u obzir prilikom pregledanja radova. Sa tim u vezi, prilazem jedan saljiv "prirucnik" profesora Predraga Janicica o tome kako treba/ne treba spremati ispit iz (tada) Osnova Geometrije (cenim da bi nekoga to moglo da zanima (mislim i na Bojana tom prilikom)).
[ berazorica @ 08.02.2012. 19:28 ] @
Meni je ova priča sa geometrijom i analitičkom geometrijom pala na pamet zato što sam jednom prilikom zatražila pomoć kolege oko jednog geometrijskog zadatka i on je odmah uočio rešenje preko vektora, jer mu je taj način razmišljanja bliži, mada je ubrzo "izbacio" i očekivano rešenje. Inače, svesna sam da poređenje nije sasvim odgovarajuće.
Sonec
Presladak je "priručnik", naročito neke od metoda! ("Ko zna dobro da razlikuje ključno od trivijalnog rizikuje da položi!")  [Ovu poruku je menjao berazorica dana 08.02.2012. u 20:42 GMT+1]
[Ovu poruku je menjao berazorica dana 08.02.2012. u 20:42 GMT+1][ darkosos @ 08.02.2012. 20:42 ] @
Slazem se da "nekoriscenje pravila" nije bogznakakav pedagoski metod. Ali bih razdvojio zaobilazenje tematike predmeta od pukog snalazenja.
Izostavljanje lopitala u ovom slucaju tera resavaca da se "snadje", bez obzira sto pritom pokazuje znanje ostalih metoda resavanja. To onda i nije nesto pedagoski... I sto rece Bojan, moze "pravilnom primenom" da suzbije slobodu resavanja problema. Dakle slazem se da je u ovom slucaju bezveze izostaviti lopitala. Mozda da je receno, resiti na bar 2 nacina :)
Ali mi se ne cini dobrim da se zaobilazi tematika predmeta, tako sto se resi u nekoj srodnoj oblasti. Mozda neko moze topologijom da resi algebarski problem? Ili da sve zadatke osnova geometrije resi analitickom (slazem se da je malo verovatno, ali opet...). Ako bi postavljac hteo da bude precizan do kraja, mogao bi da kaze: resiti metodama predmeta koji se polaze :) Ili ako zeli da popusti nekim sirokim dusama, moze da kaze: resiti vise od pola zadataka metodama predmeta koji se polaze...
Ovo "suzavanje" je svakako primereno osnovnim studijama.
[ Nedeljko @ 08.02.2012. 21:13 ] @
Citat: Predrag Janičić, Srđan Vukmirović: 2.2 Metoda pogrešne discipline
Na kursu Osnovi geometrije izučava se klasičcna, sintetička geometrija i u teoremama i zadacima se mogu koristiti samo tehnike koje odgovaraju takvom zasnivanju. Ukoliko želite da padnete na pismenom ispitu, iskoristite prethodnu činjenicu i svoje rešenje zasnujte na znanju iz neke druge matematičke discipline. Primena znanja iz trigonometrije ili iz analitičke geometrije (uz obavezno korišćenje transformacija koordinata ili krivih drugog reda) je očigledna podmetoda, ali već suviše eksploatisan. Budite originalni - svoje rešenje zasnujte na nekim još neočekivanijim tehnikama.
Ovo je očigledna glupost. U matematici je suština da se zna šta je zadatak i da se on reši, kako god, samo korektno. U kursu u kome se izučava aksiomatsko zasnivanje geometrije prirodna formulacija zadatka bi trebala da bude da se dokaže da nešto sledi iz usvojenih aksioma. E, sad, kako će student dokazati da to sledi iz tih aksioma, to je njegova stvar.
Jedan od ciljeva tog kursa je bio da se razume aksiomatski metod. Ne samo da je savršeno nepotrebno tupiti geometriju aksiomatski da bi se naučilo šta je aksiomatski metod, jer se on može savladati na primeru bilo koje aksiomatske teorije (na algebri se rade npr. teorije grupa, prstena i polja, a cela analiza se izvodi iz aksioma polja realnih brojeva), već se na ovaj način razumevanje aksiomatske metode unazađuje, pa studenti shvataju aksiomatski metod kao "ono bez trigonometrije i koordinata", a ne kao teoriju u kojoj se definišu izvedeni pojmovi preko polaznih i u kojoj se dokazuju teoreme iz aksioma.
Ako neko zna da reši zadatak analitički, rešiće ga i sintetički korišćenjem teorema Pitagore i Talesa. Naime, može se dokazati da u prostoru postoje bar tri mežusobno upravne prave, bar dve tačke A i B (čije se rastojanje uzima za jedinično), da se bilo kojim takvim izborom uvodi bijekcija između skupa tačaka prostora i R 3 u kojoj je skup jednačina ravni jednak skupu netrivijalnih linearnih jednačina itd, to jest moguće je koordinatni sistem uvesti kao izvedeni pojam iz polaznih i dokazati pomoću aksioma osobine geometrijskih pojmova u tom koordinatnom sistemu kao teoreme. Štaviše, pomenutim pristupom je moguće dokazati da euklidska geometrija ima do na izomorfizam tačno jedan model. Kome to nije jasno, taj nije razumeo sintetičku geometriju, pa makar bio profesor sintetičke geometrije.
Kada se kaže "naći primer objekta sa osobinom P", onda takav objekat svakako treba konstruisati, a ako neko želi preciznu formulaciju tog zadatka, postoji intuicionistička logika koja takve zadatke opisuje. Ako se kaže "primenom tvrđenja A dokazati tvrđenje B", postoji relevantna logika koja opisuje takve zadatke. Neka se tako lepo gospoda koja propagiraju ideju o "pogrešnoj disciplini" izjasne dajući precizan okvir rešavanja njihovih zadataka. Ovako, postavka nema nikakvog logičkog smisla. [ Bojan Basic @ 09.02.2012. 01:00 ] @
Citat: Sonec:
Sve je to lepo, ali, ako bi neko zeleo da resi zadatak tako sto ce dati iskaz i dokaz Lopitalovog pravila (naravno, tom prilikom ne zvati ga tako) trebalo bi mu dosta vremena. Sam dokaz Lopitalovog pravila (u full paketu, e sad, ako se limes svodi na samo poseban slucaj onda naravno treba manje vremena) nije uopste lak, to je jedno celo ispitno pitanje iz Analize 1 (preciznije, Analiza 1a). Dokaz koji je meni poznat (i koji sam ja ucio) ima bar 2 pune strane A4 formata, pri cemu su se neke strane nejednakosti (i slicno) radile na dualan nacin, pa nisu navodjene.
Ako u pola noći umeš da izrecituješ taj dokaz, verovatno bi ti trebalo dvadesetak minuta da ga ispišeš u celini(a ako ti je zapravo neophodan samo specijalan slučaj, onda još manje vremena). Ukoliko ti za svođenje limesa na tablični treba više od tih dvadesetak minuta (a što je vrlo lako moguće — štaviše, moguće je i da uopšte nisi u stanju da za vreme trajanja ispita rešiš zadatak na „predviđen“ način), onda se ovo očigledno isplati.
Citat: Sonec:
Dalje, pitanje je koliko bi studenata (ako bi htelo da uradi ovaj zadatak ovom metodom) znalo da da dokaz Lopitalovog pravila, ja sam siguran da bi to mozda znalo 5 do 7 ljudi na 200 studenata, jer ce 90% studenata poceti sa spremanjem usmenog tek posle pismenog, tako da nisu ni gledali dati dokaz.
Naravno. Ali ako su ovakve stvari česta pojava, onda studente neće mrzeti da namenski nauče taj jedan dokaz (rekoh gore — makar napamet, bez ikakvog razumevanja), i time sebi praktično rezervišu urađen zadatak na ispitu.
Citat: Sonec:
I u ovom zadatku, da, tacno je, treba 2 reda primenom Lopitalovog pravila, ali kakva, prvom prilikom kada se koristi Lopital ne dobije se tako rogobatan izraz, ali kada se na taj novonostali izraz primeni ponovo Lopital dobije se jedan poveliki izraz, za cije racunanje (tj. dolazenja do njega) treba dosta vremena.
I dalje sam siguran da bi mnogi znatno brže uradili to, računajući i vreme za ispis dokaza Lopitala, nego što bi rešili limes svođenjem na tablične (ako uopšte uspeju!).
Citat: Sonec:
Ali, kao sto kazes, sve zavisi i od fakulteta do fakulteta, konkretno, ako je u pitanju matematicki fakultet i ako je receno da ne sme da se koristi Lopital onda tako treba i postupiti (tj. nema nikakvog navodjenja pomocnih dokaza Lopitala i slicno), jer, ako se na matematickom fakultetu ne uradi na taj nacin (bez Lopitala), a gde ce onda da se uradi? (da nece mozda na poljoprivrednom (bez ikakvog potcenjivanja fakulteta)).
Ne slažem se. Baš se na matematičkom fakultetu od postavljača zadataka očekuje da ume adekvatno postaviti zadatak — to jest, ako neće da vidi Lopitala u rešenju, da onda postavi zadatak u kome korišćenje Lopitalovog pravila ne vodi nigde. Da iskoristim upravo ovaj tvoj argument: ako na matematičkom fakultetu ispitivač ne ume da postavi zadatak u kom Lopital ne pomaže, a gde će onda umeti?
Druga stvar: na matematičkom fakultetu predavači bi najpre morali znati da postavka „rešiti bez korišćenja Lopitalovog pravila“ ne znači ništa, jer je nedefinisana. Zaista, šta to znači? Rešiti zadatak ne pozivajući se na Lopitalovo pravilo, urađeno tokom predavanja? Eno, ja sam u prethodnoj poruci ponudio rešenje koje radi upravo to (pa je opet njegova validnost sumnjiva). Zamislimo da je Johan Bernuli (koji je izumeo Lopitalovo pravilo) dobio na ispitu baš isti ovaj limes o kom mi sad diskutujemo, i da ga je dokazao baš onako kako sam ja predložio. Za takvo rešenje sigurno se ne bi moglo reći da je nastalo „korišćenjem Lopitalovog pravila“ — jer Lopitalovo pravilo do tog momenta nije postojalo. Dakle, ne može se ni sada reći (samo na osnovu toga što je prošlo nekih tristotinak godina) da se to rešenje „poziva na Lopitalovo pravilo“ (ne poziva se ni na šta — ono je, kako bi se reklo na engleskom, self-contained). A opet, takvo rešenje verovatno ne bi priznao onaj što je mudro napisao „rešiti bez korišćenja Lopitalovog pravila“. Zato i kažem da je matematički fakultet (bilo koji, zato i pišem malim slovom) prvi gde se ovakve stvari ne bi smele dešavati.
I treća stvar: matematički fakultet uči studente matematičkom načinu razmišljanja. Matematički način razmišljanja jeste: „Ukoliko pretpostavimo da važi ovo, onda dobijamo da važi ovo“. Matematički način razmišljanja nije: „Ukoliko pretpostavimo da važi ovo, onda iako dobijamo da važi ovo, mi zapravo nećemo to na taj način da dobijemo, nego na neki drugi način“.
Citat: Sonec:
Sto se tice same geometrije (posto smo/ste se dotakli i toga) na matematickom fakultetu u Beogradu je iz Geometrije 2 (geometrija poretka, euklidska, hiperbolicka) izricito receno i stavljeno do znanje da je zabranjena upotreba analiticke geometrije, trigonometrije i slicnih "metoda", i da takva resenja nece biti uzimana u obzir prilikom pregledanja radova.
Možeš li mi ti objasniti kako se tačno definiše rešavanje zadataka ovim ili onim metodom? (I zašto si uopšte reč „metoda“ stavio pod navodnike?) Ajde, za trigonometriju se možda i možemo razumeti: zabranjeno je da se bilo gde u rešenju pojavljuju slova S, I, N jedno za drugim u tom poretku (i slično za ostale trigonometrijske funkcije), ali kako precizno definisati šta znači „rešenje korišćenjem analitičke geometrije“? Zabranjeno je pominjati koordinatni sistem? Dobro, lako će se rešenje iz analitičke geometrije ispisati i bez upotrebe koordinatnog sistema. Zabranjeno je koristiti Pitagorinu teoremu? Hm, to bi ipak bilo malo preterano, onda bi otpala i mnoga rešenja koja jesu „politički podobna“. Evo, stvarno, ko će da mi objasni šta tačno podrazumeva zabrana korišćenja analitičke geometrije? (Nedeljko je naveo još neka vrlo zanimljiva zapažanja u vezi baš s ovim konkretnim pitanjem.)
Naravno, svi mi otprilike umemo da razlučimo šta je rešenje korišćenjem analitičke geometrije (trigonometrije itd.), a šta elementarno rešenje. Ali u matematici nema razlučivanja „otprilike“, sve mora biti strogo definisano.
Citat: Sonec:
Sa tim u vezi, prilazem jedan saljiv "prirucnik" profesora Predraga Janicica o tome kako treba/ne treba spremati ispit iz (tada) Osnova Geometrije (cenim da bi nekoga to moglo da zanima (mislim i na Bojana tom prilikom)).
„Priručnik“ mi jeste bio zanimljiv, zahvaljujem. I odmah dodajem da se u njemu nalaze neke stvari s kojima se suštinski ne slažem — od kojih je ovde od relevantnosti, naravno, ovo što je Nedeljko već komentarisao, a o čemu i pričamo sve vreme.
Citat: darkosos:
Mozda da je receno, resiti na bar 2 nacina : )
Rešiću ti ja na pet načina, a da pritom nijedan nije svođenjem na tablične limese. I šta ćemo onda? 
Citat: darkosos:
Ali mi se ne cini dobrim da se zaobilazi tematika predmeta, tako sto se resi u nekoj srodnoj oblasti. Mozda neko moze topologijom da resi algebarski problem? Ili da sve zadatke osnova geometrije resi analitickom (slazem se da je malo verovatno, ali opet...).
Po mom mišljenju, svrha bilo kog predmeta jeste da osposobi studente za rešavanje problema koji po postavci spadaju u taj predmet. A ako ispitivač ne želi rešenja koja se zasnivaju na drugim oblastima, smatram njegovom dužnošću da onda postavi probleme kod kojih poznavanje drugačijih metoda ne pomaže. Zadaci tipa „rešiti ovo metodom A a ne metodom B“ neminovno vode do jednog od sledeća dva zaključka:
1) ispitivač ne zna da postavi zadatak kod kog metod B ne vodi ka rešenju, već jedino metod A;
2) zaista ne postoji zadatak kod kog metod B ne vodi ka rešenju, već jedino metod A.
U prvom slučaju diskutabilna je sposobnost ispitivača da na pravi način objasni ispitivanom čemu služi metod A — ispada da je jedina svrha metoda A rešavanje zadataka u onim situacijama kad je metod B izričito zabranjen bez posebnog razloga!? Drugi slučaj još je gori: to bi značilo da je metod A stvarno beskoristan i da stvarno služi isključivo ispunjavanju bubica ispitivača (jer — zašto bi se metod A uopšte izučavao, ako metod B uvek može brže rešiti postavljen problem?). [ Sonec @ 09.02.2012. 02:00 ] @
Sto mrzim kad neko ovako isecka post, pa analizira svaku recenicu ko da je... (zaboravi) 
Sad cu morati i ja tebi istom merom da vratim (msm na cepkanje  )
Citat: Bojan Basic: Ali ako su ovakve stvari česta pojava, onda studente neće mrzeti da namenski nauče taj jedan dokaz (rekoh gore — makar napamet, bez ikakvog razumevanja), i time sebi praktično rezervišu urađen zadatak na ispitu.
Ajde ti (dobro, ne moras ti, ti imas veci autoritet kod studenata) predlozi ovo nekom studentu, ima samo da te pogleda blentavo i da te pita: "Jesi ti lud mozda?"
Citat: Bojan Basic: Baš se na matematičkom fakultetu od postavljača zadataka očekuje da ume adekvatno postaviti zadatak — to jest, ako neće da vidi Lopitala u rešenju, da onda postavi zadatak u kome korišćenje Lopitalovog pravila ne vodi nigde. Da iskoristim upravo ovaj tvoj argument: ako na matematičkom fakultetu ispitivač ne ume da postavi zadatak u kom Lopital ne pomaže, a gde će onda umeti?
Iskreno, ovo se i ne bi moglo zameriti zadacima sa matematickog fakulteta u Beogradu (stalno potenciram "u Beogradu" jer ne znam kako je na ostalim matematickim fakultetima, a ne da bih dizao fakultet u nebesa). Dosada nisam naisao na neki takav zadatak (ako cemo iz limesa) gde se precizira da se ne sme koristiti Lopital. Zadaci iz limesa se obicno zadaju tako da se primenom Lopitala (ako je "dozvoljen" u toj situaciji (msm na oblik limesa)) ne dovodi do priblizavanja resenju, pre bi se moglo reklo, da je to jedna beskonacna petlja.
U sustini, ne postoji ogranicavanje studenata na to kojom metodom treba dodji do resenja (npr. stalno smo trazili kosu asimptotu funkcije preko razvoja u Tejlorov red, asistent nam je rekao pred ispit da mozemo da radimo i na standardan nacin (koji nam je poznat iz srednje skole)), sto se tice samog Lopitala, ni tu nije bilo zabrane, tacnije, mi Lopitala nismo ni radili nista posebno (jedan, do dva primera u vrh glave). Ali, ako hocemo posteno, npr. vec iz spomenute Geometrije 2 postoje ogranicenja na "metode" koje smemo da koristimo.
Citat: Bojan Basic: I treća stvar: matematički fakultet uči studente matematičkom načinu razmišljanja. Matematički način razmišljanja jeste: „Ukoliko pretpostavimo da važi ovo, onda dobijamo da važi ovo“. Matematički način razmišljanja nije: „Ukoliko pretpostavimo da važi ovo, onda iako dobijamo da važi ovo, mi zapravo nećemo to na taj način da dobijemo, nego na neki drugi način“.
Malo generalizujes stvari.
Citat: Bojan Basic:Možeš li mi ti objasniti kako se tačno definiše rešavanje zadataka ovim ili onim metodom? (I zašto si uopšte reč „metoda“ stavio pod navodnike?).... Zabranjeno je koristiti Pitagorinu teoremu?
Ne mogu, niti imam nameru, da ti objasnjavam kako se definise resavanje zadataka odredjenom metodom.
Rec metoda sam stavio pod navodnike jer nisam znao kako da okarakterisem razlicite postupke resavanja zadataka, bez navodnika mi nije prijalo, a nisam stavio pod navodnike da bih time pokazao da se ne slazem/potcenjujem taj nacin.
Dozvoljeno je koriscenje Pitagorine teoreme (ali sumnjam da ce ona sta koristiti u zadacima koji se zadaju na ispitu (radjen je samo jedan primer gde se koristila Pitagorina teorema, i posle joj se gubi trag)).
Citat: Bojan Basic: Evo, stvarno, ko će da mi objasni šta tačno podrazumeva zabrana korišćenja analitičke geometrije?
Koordinatni sistem i vektori prvenstveno, al ako hoces da znas tacno onda pitaj jednog asistenta (tacnije "saradnika u nastavi") na MATF u bg, mislim da znas na koga mislim.
Citat: Bojan Basic: „Priručnik“ mi jeste bio zanimljiv, zahvaljujem. I odmah dodajem da se u njemu nalaze neke stvari s kojima se suštinski ne slažem — od kojih je ovde od relevantnosti, naravno, ovo što je Nedeljko već komentarisao, a o čemu i pričamo sve vreme.
"Prirucnik" sam prilozio cisto jer je meni bio zanimljiv, a malo i ima veze sa temom (dobro, ne bas sa imenom teme, al sa celom diskusijom). Nisam ga stavljao da bih na taj nacin potkrepljivao neka moja razmisljanja. [ darkosos @ 09.02.2012. 07:56 ] @
Citat: Rešiću ti ja na pet načina, a da pritom nijedan nije svođenjem na tablične limese. I šta ćemo onda?
Onda necemo nista jer si promasio cilj :) Poenta je bila da ako je jedan od nacina (najlaksi) lopital, onda mora da resi na jos jedan. Ako resi na 2 koji nije lopital, onda je cilj postavljaca duplo postignut :) [ Nedeljko @ 09.02.2012. 10:23 ] @
Postoji linearna logika koja broji koliko je koja aksioma bila puta upotrebljena u dokazu teoreme. Međutim, ovde se ne radi o tome, već da ocenjivač ne priznaje rešenje zadatka, ne zato što traženo tvrđenje nije izvedeno iz aksioma, već zato što je u dokazu tvrđenja A iz usvojenih aksioma izvedeno tvrđenje B iz tih istih aksioma i onda je tvrđenje A dokazano pozivanjem na aksiome i tvrđenje B, pri čemu tvrđenje B nije politički podobno. E, to je nešto što nema veze sa aksiomatskim pristupom, koji dopušta sve korektne puteve izvođenja tvrđenja iz aksioma.
Student na ispitu mor aimati smislenu i jasnu formulaciju onoga što treba da uradi. Recimo, dozvoljeno je koristiti usvojene aksiome euklidske geometrije i određene teoreme (na primer one koje su dokazane na predavanjima i vežbama) bez dokaza, tj. kao aksiome i sve što student dokaže u okviru svog pismenog zadatka.
E, sad neka takvi ocenjivači objasne npr. Aleksandru Iviću koji se bavi analitičkom teorijom brojeva da koristi "metod pogrešne discipline", jer zaboga, dokazuje tvrđenja o prirodnim brojevima metodama realne i kompleksne analize ili neka obore Vajlsov dokaz velike Fermaove teoreme metodama algebarske geometrije jer je to sa stanovišta teorije brojeva "pogrešna disciplina".
Koliko mi je poznato, konstrukcija strukture prirodnih brojeva nije svodljiva na jednostavnije matematičke konstrukcije, pa se postojanje bar jednog modela Peanove aritmetike zapravo postulira kao jedna od aksioma teorije skupova ZFC (zapravo, aksiomom beskonačnosti se postulira postojanje bar jednog induktivnog skupa, što je uz ostale aksiome teorije skupova ekvivalentno postojanju bar jednog modela Peano aritmetike). Ja ne znam ni za jedan drugi pristup uvođenja prirodnih brojeva u matematici kao nauci, tako da ako Endriju Vajls nije dokazao da je velika Fermaova teorema posledica aksioma Peanove aritmetike, onda je on nije ni dokazao.
Naravno, Endriju Vajls nije u svom radu počeo od aksioma i izvodio elementarne stavove, već je pošao od nekog nivoa, tj. pretodno dokazanih teorema i koristio prethodno uveden pojmove, ali ako ne postoji prelaz od aksioma do velike Fermaove teoreme, onda to jednostavno nije to, jer nije dokaz u strukturi prirodnih brojeva onako kako je ona definisana u matematici.
Naravno, taj prelaz postoji i svestan ga je svako ko je razumeo gradivo koje se izlaže na matematičkim fakultetima širom sveta.
[ Nedeljko @ 09.02.2012. 11:40 ] @
"Metod pogrešne metode" bih uporedio sa situacijom u kojoj je na ispitu iz algebre zadat zadatak da se dokaže da ne postoji prosta grupa reda 200, pa ako student reši zadatak primenom teorema Silova kako je asistent zamislio, onda u redu, a ako nađe alternativno rešenje ono se ne priznaje jer odakle njemu pravo da razmišlja drugačije.
[ berazorica @ 09.02.2012. 12:22 ] @
u mojoj svesci:
"Feit-Thompson
Sve grupe neparnog reda su rešive.
dokazano 1963.
napomena: ne koristiti na pismenom!"
[ Nedeljko @ 09.02.2012. 14:24 ] @
Pa, u redu, to znači da se ne koristi bez dokaza, a ako na pismenom nema dovoljno vremena da se raspiše dokaz, onda to praktično znači da se ne može ni koristiti na pismenom. No, ako neko ipak uspe da dokaže tu teoremu na pismenom i da je upotrebi, ja bih mu odmah dao 10 bez razmišljanja, a neko ko ne bi, u svakom slučaju ne bi smeo da išta zakine.
[ darkosos @ 09.02.2012. 15:02 ] @
Citat: Bojan Basic: Po mom mišljenju, svrha bilo kog predmeta jeste da osposobi studente za rešavanje problema koji po postavci spadaju u taj predmet.
Slazem se analizom (a ko ne bi kad je dobra :) ali bih dodao i da je svrha predmeta i ucenje metoda tog predmeta. Dakle, zaobilazenje metoda moze biti i posledica nepoznavanja istih, ma koliko neko bio domisljat i uradio nesto na drugaciji nacin... Onda je verovatno pitanje karaktera ispitivaca... Opet kazem, ovo sve vazi za osnovne studije... Svakako postojji potreba da se nagradi domisljatost i sirina, ali mislim da ovo nije pravi nacin. [ Nedeljko @ 09.02.2012. 16:36 ] @
Ja bih malo korigovao ovaj Bojanov stav. Po mom mišljenju, na predmetu treba da se osposobljava za rešavanje problema koji po postavci ne spadaju u taj predmet, ali se mogu rešiti alatima tog predmeta. Na primer, imam realan pronblem (recimo nematematički problem koji se može rešiti pomoću matematike), prepoznam šta bi od alata trebao da koristim, modeliram ga i rešim. E, sad, ako student zna da rešava takve probleme, u čemu je problem? Kakve veze ima ako ne može da reši problem profesorovom metodom, ako zna da ga reši?
[ berazorica @ 09.02.2012. 18:43 ] @
Citat: Nedeljko: Pa, u redu, to znači da se ne koristi bez dokaza, a ako na pismenom nema dovoljno vremena da se raspiše dokaz, onda to praktično znači da se ne može ni koristiti na pismenom. No, ako neko ipak uspe da dokaže tu teoremu na pismenom i da je upotrebi, ja bih mu odmah dao 10 bez razmišljanja, a neko ko ne bi, u svakom slučaju ne bi smeo da išta zakine.
U stvari, piše i da je dokaz dat na oko 250 strana.  [ Nedeljko @ 09.02.2012. 19:45 ] @
Ali, ako student nađe svoj dokaz na tri strane i tako reši zadatak, šta onda? Da dobije nula bodova, jer asistent nije to tako zamislio?
Sećam se sledeće situacije kada sam polagao ispit iz distribucija i parcijalnih jednačina: zadatak je bio da se dokaže da je pod nekim pretpostavkama neka realna funkcija dve promenljive harmonijska, što je bilo vrlo lako dokazivo preko kompleksne analize. Asistent je naglasio da se ne koristi kompleksna analiza, a onda se ispravio sa rečima "ustvari može, ali samo nešto malo". Pitao sam šta je to "nešto malo", ali je on odbio da odgovori jer bi time otkrio svoju zamisao. Onda sam pokušao da rešim zadatak na neki način i pitao ga da li teorema A spada u to "nešto malo". Odgovor je bio negativan. Onda sam našao rešenje preko još prostije teoreme B kompleksne analize i pitao da li ona spada u to "nešto malo". Odgovor je ponovo bio negativan. Onda sam našao rešenje preko još prostijeg C, za šta se napokon ispostavilo da spada u to zamišljeno "nešto malo". Tako sam pogubio silno vreme na ispitu čitajući njegove misli.
[ Bojan Basic @ 09.02.2012. 23:11 ] @
Citat: Sonec:
Sto mrzim kad neko ovako isecka post, pa analizira svaku recenicu ko da je... (zaboravi) 
Matematičari su temeljni ljudi. 
Citat: Sonec:
Ajde ti (dobro, ne moras ti, ti imas veci autoritet kod studenata) predlozi ovo nekom studentu, ima samo da te pogleda blentavo i da te pita: "Jesi ti lud mozda?"
Čekaj, jesmo li se sigurno razumeli? Dakle, ono što ja pričam je sledeće. Zamislili smo da student izbor između sledeće dve varijante:
a) da nauči dve stranice iz knjige, a onda na pismenom ispitu, u sklopu jednog zadatka, mehanički reprodukuje te dve strane, i uz pride dopisana dva reda obezbedi sebi rešenje jednog zadatka maltene bez ikakvog mozganja;
b) da poštedi sebe učenja te dve stranice, već da se pouzda kako će isključivo svojom pronicljivošću uspeti da na ispitu reši zadatak na način koji je postavljač zamislio (a što može biti neuporedivo teže od prethodne varijante).
Ti tvrdiš da studenti smatraju ludim onoga ko uviđa prednost varijante a)? Stvarno? Ja sam, eto, prilično uveren da bi u pretpostavljenoj situaciji skoro svi studenti odabrali baš varijantu a). Loši studenti — zato što su loši, teško im je da bilo šta samostalno izmozgaju, i zato će ići na varijantu a), koja minimalizuje mozganje. Dobri studenti — e, oni bi možda i bili u stanju da sve izmozgaju prema varijanti b), ali zašto bi to radili kada i njima varijanta a) štedi vreme?
Citat: Sonec:
Iskreno, ovo se i ne bi moglo zameriti zadacima sa matematickog fakulteta u Beogradu (stalno potenciram "u Beogradu" jer ne znam kako je na ostalim matematickim fakultetima, a ne da bih dizao fakultet u nebesa). Dosada nisam naisao na neki takav zadatak (ako cemo iz limesa) gde se precizira da se ne sme koristiti Lopital.
To je lepo. Znači da se ovaj fakultet ipak bar po tome izdvaja (u pozitivnom smeru, naravno) od drugih fakulteta na kojima se takođe obrađuju limesi.
Citat: Sonec:
Malo generalizujes stvari.
Pojasni?
Citat: Sonec:
Koordinatni sistem i vektori prvenstveno, al ako hoces da znas tacno onda pitaj jednog asistenta (tacnije "saradnika u nastavi") na MATF u bg, mislim da znas na koga mislim.
Eh, pa ne može tako.  U ovoj diskusiji ti braniš stav da je u redu (bar u određenim okolnostima) davati zadatke sa zabranjenim metodima. Samim tim, na tebi je da odgovoriš na komentare koji ističu probleme u tvom stavu.
Pominjanje koordinatnog sistema može se vrlo lako zaobići (rekoh to već u nekoj ranijoj poruci, a i Nedeljko se osvrtao na taj deo), a nisu ni vektori mnogo teži za zaobilaženje.
Citat: Nedeljko:
Recimo, dozvoljeno je koristiti usvojene aksiome euklidske geometrije i određene teoreme (na primer one koje su dokazane na predavanjima i vežbama) bez dokaza, tj. kao aksiome i sve što student dokaže u okviru svog pismenog zadatka.
Modifikujmo neznatno ovu tvoju definiciju: „...određene teoreme (na primer one koje su dokazane na predavanjima i vežbama, izuzimajući Lopitalovo pravilo)...“ I ispada da ovako stvarno dobijamo način da se konkretno zabrani Lopitalovo pravilo. No, problem je što rešenje poput onoga što sam pisao u ovoj poruci zadovoljava sve ove restrikcije, a opet osnovano sumnjam da ne bi bilo priznato u slučaju da zadatak zahteva izračunavanje limesa „bez upotrebe Lopitalovog pravila“. I dalje ne vidim kako sročiti smislenu i jasnu formulaciju zabrane korišćenja Lopitalovog pravila — u stvari, ne samo što ne vidim, već smatram da takva formulacija ne postoji (tj., da se uvek može zaobići).
Citat: berazorica:
u mojoj svesci:
"Feit-Thompson
Sve grupe neparnog reda su rešive.
dokazano 1963.
napomena: ne koristiti na pismenom!"
Ovo ipak smatram manje lošom praksom od zabrane korišćenja Lopitalovog pravila, budući da se dokaz ove teoreme ne radi na času, niti bi uopšte mogao da se radi. Ali, naravno, ukoliko bi se nekim čudom desilo da student na licu mesta na ispitu najpre dokaže ovu teoremu pa je potom iskoristi — smatram da bi to bilo neophodno priznati (što je Nedeljko već i rekao). Jasno, šanse za to su izuzetno male, budući da bi takav dokaz morao biti stotinak puta kraći od najkraćeg do sada poznatog dokaza.
No, rekoh gore da, dakle, ovakvu restrikciju smatram manje lošom praksom od zabrane korišćenja Lopitalovog pravila — ali i dalje se čak ni s ovakvom restrikcijom lično ne slažem. Imam i sopstvenih primera da potkrepim ovaj stav. Na kolokvijumu iz teorije brojeva jednom prilikom sam dao zadatak u čijem se rešenju treba pozvati na čuvenu teoremu Erdeša i Selfridža o proizvodu uzastopnih prirodnih brojeva. (U pitanju je teorema koja je rešila 250 godina star problem. Njen dokaz, istina, ne zauzima baš stotine stranica, ali zauzima desetak, i ne radi se u sklopu predmeta. Teoremu sam tokom nastave naveo, rekao ko ju je i kada dokazao, i rekao studentima da je smeju koristiti na kolokvijumu — kao, uostalom, i sve druge.) Ne samo da sam, naravno, priznavao rešenja preko dotične teoreme, već je upravo to bila i moja zamisao, i uopšte ne znam da li postoji neko rešenje koje zahteva skromniji aparat.
Evo još jednog primera. Imam spremna dva zadatka u kojima se tokom rešenja treba na određenom mestu pozvati na veliku Fermaovu teoremu. Te zadatke verovatno ću postaviti nekoj od nadolazećih generacija studenata. Jasno je, naravno, da se dokaz te teoreme ne može raditi na času  — ali ne vidim ništa sporno da se ona formuliše na času, kaže se gde je i kada dokazana (zapravo, za konkretan primer velike Fermaove teoreme, u programu predmeta predviđeno je i nešto dodatne priče o noj, ne samo suvi faktografski podaci), a potom proveri umeju li studenti da je primene u nekom zadatku.
(Dodatak: naglašavam, za zadatke iz poslednjeg pasusa rekao sam samo da ću ih „verovatno“ dati „nekad“. Dakle, ako ovo i pročita neko od aktuelnih studenata, smatram da ništa bitno ne saznaje iz te rečenice, pa zato verujem da nije ništa sporno što sam to javno napisao.)
Citat: Nedeljko:
No, ako neko ipak uspe da dokaže tu teoremu na pismenom i da je upotrebi, ja bih mu odmah dao 10 bez razmišljanja, a neko ko ne bi, u svakom slučaju ne bi smeo da išta zakine.
S desetkom ili bez nje, dodajmo da bi taj student stekao instant svetsku slavu. 
Citat: darkosos:
Onda je verovatno pitanje karaktera ispitivaca...
Od karaktera ispitivača verovatno zavisi želi li on na svome ispitu studentska rešenja zasnovana na njemu „bezveznim“ metodima. No, sad već ne znam koji put ponavljam  : ako ispitivač ne želi takva rešenja, ako želi da studentima utuvi u glavu metode svog kursa a ne „domišljatost i širinu“ — najupečatljiviji način da demonstrira važnost poznavanja dotičnih metoda upravo je postavka zadataka gde jedino one mogu dovesti do rešenja. Dakle, dužnost ispitivača je da odabere zadatke shodno onome što želi proveriti kod studenata, a nije dužnost studenata da čitaju misli i nagađaju preferencije ispitivača.
Citat: Nedeljko:
Onda sam našao rešenje preko još prostijeg C, za šta se napokon ispostavilo da spada u to zamišljeno "nešto malo".
Da li C označava Koši—Rimanove uslove?  [ Sonec @ 09.02.2012. 23:37 ] @
Ovako, kada sam rekao: predlozi ovo nekom studentu, ima samo da te pogleda blentavo i da te pita: "Jesi ti lud mozda?", mislio sam na same studente, koje bi mrzelo ovo da nauce (nemoj da mi pricas da ne bi, jer znamo da bi).
Ja sam samo izneo neko svoje misljenje vezano za tvoj uvodni post, al onda mi ti postavis novih 10 pitanja, pa ja odgovrim, pa sad ponovo neka pitanja, ne mogu ja tako, nisam u policiji da odgovaram na svakojaka pitanja.
U redu je koristiti razne drugacije metode za resavanje nekog zadataka/teorema, nemam ja nista protiv toga, ne morate da se pozivate na cuvene matematicare da bi ste dokazali svoje misljenje, idete suvise daleko. Ali, ako se predmet zove B, a vi sve zadatke resavate metodom C, koji je onda smisao predmeta B. Valjda treba da naucimo da koristimo i predmet B, a ne samo da se "izvlacimo" pomocu C.
I ne znam sto ste mene spopali da ja zastupam zabranu nekih metoda i slicno, samo sam rekao kako jeste.
Nikad nisam bio vican u raspravama/diskusijama koje su filozofskog/metodoloskog karatera, ako je u pitanju neki konkretan zadatak, teorema, dokaz, onda u redu, tu sam da se objasnimo, al o ovome zaista nemam snage i volje da se objasnjavam.
Vise se necu javljati na ovoj temi, jer se zaista osecam lose kada pisem ovo, ne prija mi.
[ Nedeljko @ 10.02.2012. 06:48 ] @
Citat: Sonec: U redu je koristiti razne drugacije metode za resavanje nekog zadataka/teorema, nemam ja nista protiv toga, ne morate da se pozivate na cuvene matematicare da bi ste dokazali svoje misljenje, idete suvise daleko. Ali, ako se predmet zove B, a vi sve zadatke resavate metodom C, koji je onda smisao predmeta B. Valjda treba da naucimo da koristimo i predmet B, a ne samo da se "izvlacimo" pomocu C.
Pa, smisao predmeta B svakako ne postoji ako se svi problemi koji se mogu njime rešiti mogu rešiti i metodom C. U tom slučaju zabrana metode C svakako neće dati smisao predmetu B, odnosno u tom slučaju predmet B treba izbaciti iz programa kao nepotreban. [ darkosos @ 10.02.2012. 07:55 ] @
Citat: Bojan Basic: Dakle, dužnost ispitivača je da odabere zadatke shodno onome što želi proveriti kod studenata, a nije dužnost studenata da čitaju misli i nagađaju preferencije ispitivača.
Potpuno slazem. Ali bih dodao i to da ako ispitivac zeli sirinu, onda opet mora da je nadje u okviru svog predmeta :)
Znaci zadatkodavalac bi mogao ovako da razmislja: hocu da kroz ove zadatke pokazu znanje i metodiku predmeta, a da kroz ovaj zadatak (namerno jednina i mnozina) pokazu sirinu. Onda, ako je toga svestan, ne bi trebalo da na umu ima metodike drugih predmeta (mozda ih student jos nije ni obradio), vec slozenije metode ili neispricane stvari koje je moguce smisliti za vreme trajanja ispita minus vreme za "obicne zadatke" :) Ako pak student iznenadi i resi nepredvidjenom metodom takav zadatak - stvar je jasna: treba ga nagraditi... Jer ako je pokazao valdanje ostalim "trivijalnim", "ispisanim" metodologijama, onda nista nije naruseno time sto je smislio resenje koje ni zadatkodavaocu nije palo na pamet. Ali ma kako resio "obicne" zadatke, ako to ne pokazuje vladanje metodikom predmeta, to bas nije svrha predmeta.
Mislim da se malo zaboravlja sledeca stvar: matematicka sirina bi trebalo da se pokazuje kada je zadatak oslobodjen granica konkretnog predmeta. Kao kad bi uveli takav predmet: resiti zadatke proizvoljnom metodom. A onda mozda na usmenom ispitati teoriju koja stoji iza datih resenja. ma kakva bila. To bi onda po meni bio pravi nacin...
Ne zelim da zvucim kao neko ko previse voli pravila, uskogrudost i slicno. Ko me poznaje, a ovde takvih nema :) zna da sam uvek trazio resenja ne obaziruci se na granice... To radim i sada, profesionalno, iako se ne bavim matematikom... Ali znam da je do takvog necega potrebno proci kroz dobar "trening" sto osnovne studije jesu. Zamislimo da, ako recimo metodom A, kojom je bilo predvidjeno da se resi zadatak, student iskoristio metodu B. Jasno je da on, ako prodje :) moze nikad ne savladati metodu A. I onda se desava da zapne na nekom sledecem problemu, koji npr moze jedino da se resi metodom A. Da li je on osposobljen da se bavi profesionalno matematikom? Pa ne bas, morace da se vrati na ucenje metode A... A ako se ne bavi profesionalno, who bre cares? :) Na onom ko zadaje zadatke, tu se slazemo, je da se potrudi da dobro obradi oblasti i metodologiju. [ Nedeljko @ 10.02.2012. 13:51 ] @
Ako postoje problemi koji se rešavaju samo metodom A, zašto onda asistent ne zada takav zadatak na ispitu? Sa druge strane, ako je student ispoljio sposobnost rešavanja mnogih klasa problema i pritom sposobnost matematičkog rasuđivanja, najmanji problem će mu u praksi biti da pogleda metodu A iz svojih starih udžbenika. Dakle, osposobljen je.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|