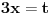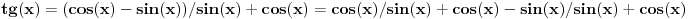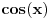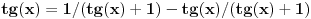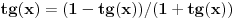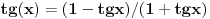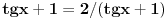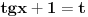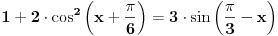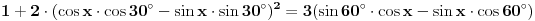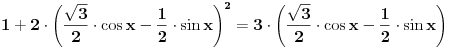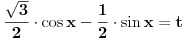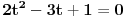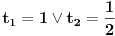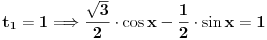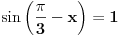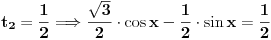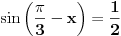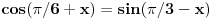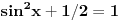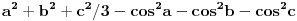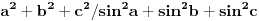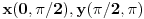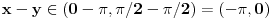[ Open93 @ 15.02.2012. 12:24 ] @
|
| Resiti jednacine:
1.) tg x= (cos x - sin x) / (cos x + sin x)
Zadaci su za prijemni na FTN ubih se resavajuci i ne ide. Pa ako moze bilo kakva smernica. HVALA!!!
[Ovu poruku je menjao Open93 dana 15.02.2012. u 13:36 GMT+1] |
[ edisnp @ 15.02.2012. 12:39 ] @
[ cikin @ 15.02.2012. 12:44 ] @
ide ovako ako sam pogresio neko nek ispravi: 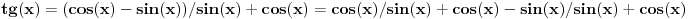 sad delis sa 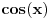 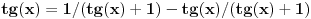 to je sad 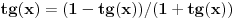 s tim da tg(x) ne sme biti -1!!! sad sam resis kvadratnu jednacinu!!! [ Open93 @ 15.02.2012. 12:48 ] @
Dotle i ja stigao al nmg nikako da resim kvadratnu jednacinu. Ako pomnozim jednacinu sa imeniocem postoji verovatnoca da cu da izgubim neka resenja.
[ cikin @ 15.02.2012. 12:55 ] @
[ Open93 @ 15.02.2012. 14:24 ] @
E Hvala ti legenda si. e mogu da kontaktiram pvt ako budem imao jos neki problem?
[ cikin @ 15.02.2012. 21:49 ] @
naravno....i ja se sad pripremam :)
[ Open93 @ 16.02.2012. 12:36 ] @
1+2cos^2(x+pi/6)=3sin(pi/3-x)
[ cikin @ 16.02.2012. 15:25 ] @
mozes i da pises 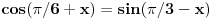 msm da je tako lakse..... [ Open93 @ 16.02.2012. 17:42 ] @
Hvala puno momci ja prebacivao sin u cos umesto da sam samo tako razvijao jednacinu. Nikad mi nece biti jasna trigonometrija. Na jedan nacin dobijem tacno resenje a na drugi nacin mi se pojavi greska otkuda ne znam ... Ako bude jos koji zadatak smaracu vas...
[ cikin @ 19.05.2012. 15:18 ] @
http://www.wolframalpha.com/in...sqrt%28cosx%5E2%2B1%2F2%29%3D2 e ja sam radio tako sto sam ovo kvadrirao, i da ne pisem dalje ispada mi 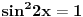 .... i to mi ne daje sva resenja, jedino da radim 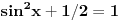 , jel ja mogu posto znam kolko moze biti max vrednost sinx ili cosx , smatrati da samo 1+1=2 (nadam se da shvatate sta sam rekao) i da u proizvoljnom trouglu 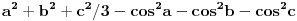 e sad 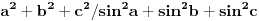 kako da znam da je to 4R^2
[Ovu poruku je menjao cikin dana 19.05.2012. u 16:29 GMT+1]
[Ovu poruku je menjao cikin dana 19.05.2012. u 16:30 GMT+1]
[ darkosos @ 20.05.2012. 10:00 ] @
A koja resenja nisi dobio? Naravno, jedan od nacina da se dobije 2 jeste da su obe potkorene velicine jednake 1, ali ne vidim kako bi to moglo da doda resenja na onosto vec imas...
[ cikin @ 20.05.2012. 12:33 ] @
hvala, ma pogresio sam kad sam racunao 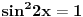 [ cikin @ 06.06.2012. 00:22 ] @
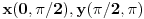 (ne znam simbol, uglavnom x i y pripadaju tom skupu) e sad samo kako da odredim u kom intervalu ce biti resenje cos(x-y) [ darkosos @ 06.06.2012. 07:54 ] @
Simbol je \in. 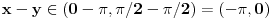 . Fora je da je najmanja moguca vrednost razlike x-y jednaka min x - max y, a najveca razlika se dobija za max x i min y. [ crnibatica @ 29.04.2013. 22:49 ] @
cos2 18+cos2 36+cos2 54+cos2 72 = ?
Ja sam isao na to da spojim prvi i poslednji i drugi i treci i dobijem 2cos^2 90 = 0
Zanima me da li je to tacno?
[ miki069 @ 29.04.2013. 23:04 ] @
Prvi i poslednji u zbiru daju 1, drugi i treći takođe 1.
Ceo zbir je 2.
[ crnibatica @ 30.04.2013. 11:30 ] @
Kako cosinus od 90 = 1 ?
[ darkosos @ 30.04.2013. 11:34 ] @
Nije cos 90 = 1, nego nije tacno da je cos2 18 + cos2 72 = cos2 90... ovo sto ti je miki069 napisao je posledica toga da je cos 18 = sin 72 i osnovnog trigonometrijskog identiteta.
[ crnibatica @ 30.04.2013. 17:40 ] @
A da ja sam sabirao, to je to onda, hvala.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|