Sta ti je konkretno problem? Pretpostavljam da ti je poznat Gausov metod? Eventulano oko ovog b+3? Ako mnozis sa tim izrazom, b ne sme biti -3, pa taj slucaj treba posebno obraditi...

Svakoj jednačini može da doda bilo koju jednačinu pomnoženu bilo kojim brojem. Recimo, od četvrte jednačine može da oduzme prvu pomnoženu sa b+3 s tim da prva jednačina ostane nepromenjena. No, ako neku jednačinu zameni tom jednačinom pomnoženom nekim brojem, onda taj broj ne sme biti nula.

Dakle, od druge jednačine oduzmi prvu pomnoženu sa 2, od treće drugu pomnoženu sa 3, od četvrte prvu pomnoženu sa b+3. Onda na isti način rešavaj sistem od poslednje tri jednačine (jer se u njemu više ne pojavljuje x). Od treće ćeš oduzeti drugu itd.

Kako ovime pravim nulu?

Ali opet, ja sada dobijam neke neverovatne brojeve vezane za parametar b. Ne umem da se oslobodim. Ovaj zadatak sam imao na prvom kolokvijumu, i nisam umeo da napravim nule, posle nisam vise ni pokusavao. I sada sam uzeo da ga uradim, jer mi se blizi ispit, ali ne ide... :/

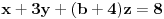
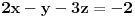
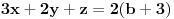
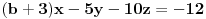
Sabereš prve dve jednačine, tada se dobije:



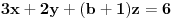
Od ove jednačine oduzmi treću, pa dobiješ:



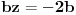
Odatle dobiješ dva moguća rešenja, ili je b=0 ili je z=-2

Dalje radiš tako što probaš oba rešenja...

P.S. Dalje koristiš sistem bez treće jednačine, jer je treća linearno zavisna od prve dve...

_{[Ovu poruku je menjao djoka_l dana 17.02.2012. u 15:30 GMT+1]}

Moram Kroneker-Kapelijevom teoremom....

Pa Kroneker-Kapelijevom teoremom, mozes kao Gausom.

a1 x1+a2 x2+a3 x3+...+an xn =a0

.........b2 x2+b3 x3+...+an xn =b0

..................c3 x3+...+cn xn=c0

I tako dalje, pravis trougao, samo sto kod Kronekera ne pises x1, x2, x3, vec samo koeficijente i slobodne clanove (a0,b0,c0...).

Mozes da menjas mesta i vrstama i kolonama.

Znaci u matrici si, pravis nule, a mislis o Gausu. :)

Srdjane, je l ti nije problem da odradis pomocu LATEX-a? Onako kako ti umes to, kao sto si mi odradio jedan sistem pre par meseci? :) Bio bih ti jako zahvalan!

Ne mogu da pisem ceo postupak. Uglavnom, sveo sam na ovo


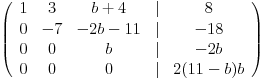
Ako je b=11, 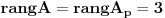=> Jedinstveno resenje.



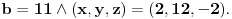
Ako je b=0, 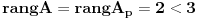=>Beskonacno resenja.



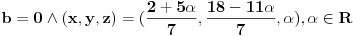
Za bilo koje drugo b nema resenja.

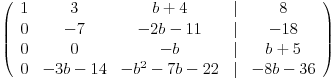
Prvu sam mnozio sa -2 i dodao je drugoj, zatim sa -3 i dodao je trecoj, i sa -(b+3) i dodao je cetvrtoj. Onda sam drugu pomnozenu sa -1 dodao trecoj, i dobija to iznad. Dalje ne znam kako... Ne znam kako da napravim jos ove dve nule..

Zameni trecu i cetvrtu, a ovo zaokruzeno ce ti dati jos jednu potrebnu nulu.

Nisam proveravao da li ti je ovo tacno, ali ako jeste, ovo sto rekoh gore je jedini logican korak.

Pogresio sam kod prosirene u trecoj vrsti: (treba 2b, a ne b+5)




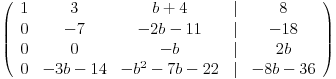
Cime treba da mnozim sada da bih napravio tu nulu koju ti vidis kada zamenim mesta ovim dvema koje si zaokruzio?

_{[Ovu poruku je menjao patkan1992 dana 18.02.2012. u 19:34 GMT+1]}

Druga puta (3b+14)+Cetvrta puta -7.

A trecoj i cetvrtoj zameni mesta (mozes pre ovog gore, mozes i posle).

Mozda taj poslednji potez i nije neophodan; s obzirom da taj kvadratni trinom nema nule, poslednji red ne donosi razliku izmedju ranga matrice sistema i ranga prosirene matrice...
Kada se analizira i resi sistem po prve tri jednacine, samo treba zameniti u tu cetvrtu da se vidi da li je to ok...

EDIT: Nisam lepo procitao. :)


Hvala puno!