1. Iz pretpostavke da je rastuća funkcija sledi da postoji i da je . No, ako bi za svako važilo da je i još i , onda bi funkcija bila neprekidna. Dakle, ako je prekidna, mora bar jedan od tih uslova da se negde naruši.

2. Pretpostavi da je . Gde bi moglo da bude obzirom da je funkcija rastuća?

Ovako je ocigledno...

Dakle, pretpostavim da je . Ako je , onda je i to je kontradikcija. Ako je , onda je , i to se opet kosi sa izborom broja . Ako je , onda je , tj. , sto opet ne moze.
Je l' to to? Pa nije bas tako ocigledno, ima malo da se pise...

Ako je onda je , a ne može biti . Ako je , onda je zbog činjenice da ne opada ispunjeno , što opet nije moguće.

Za monotonon neopadajuću funkciju važi . Zaista, ako je , onda iz za sve sledi da je . Ako važi , onda postoji takvo da je , pa za i važi , odnosno , pa je , što opet nije moguće.

_{[Ovu poruku je menjao Nedeljko dana 18.02.2012. u 20:57 GMT+1]}

Sad mi je otprilike jasno, hvala. A moze li da bude ? Posto bi onda bilo , a to valjda ne moze?

Mozda jedan malo drugaciji pristup (usput, nestala je slika koju sam okacio...):

Ako je f monotona, onda ima i osobinu da ako je f(c) izmedju f(a) i f(b), onda je i c izmedju a i b (primenom kontrapozicije na standardni x<y => f(x)<f(y) i slicno za opadajucu).
Tako, ako kao u navedenom scenariju, f ima prekid i f(d_) < f(d), onda imamo sledece:

, pri cemu je ovo poslednje posledica toga da je f funkcija.
Ovo je napisano manje formalno, jer je f(d_) zapravo granicna vrednost, ali u tom procesu, posmatrano c zaista upada u intervale koji konvergiraju ka [d,d]...

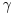
To dakle govori da prethodno pominjano ne moze biti razlicito od f(d) u slucaju da f ima prekid. Tako, u postavljenom scenariju, kada je f monotona, osobina koja je data kao drugi uslov u stavu je uzajamno iskljuciva sa postojanjem prekida. Dakle ako je ispunjen taj uslov, f ne moze imati prekid pa je neprekidna.

Ispravljeno.

Može da bude . U svakom slučaju će se tada svesti na , što je OK jer je .