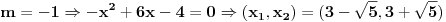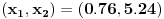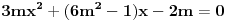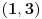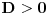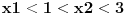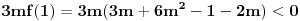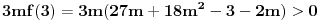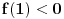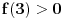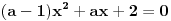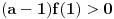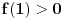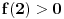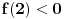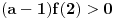|
|
[ Milesija @ 18.02.2012. 14:07 ] @
|
| Za koje vrednosti realnog parametra m su rešenja jednačine mx^2-2(m-2)x+m-3=0 istog znaka
Rešenje: Pošto koeficijent uz kvadratni član zavisi od parametra, onda on mora biti različit od 0 tj. m≠0.
a) Rešenja kvadratne jednačine su istog znaka, akko je:
D≥0 ∧ x_1∙x_2>0, onda je:
D=(〖-2(m-2))〗^2-4∙m∙(m-3)≥0
D=-m+4≥0 tj. m≤4 (1)
x_1 * x_2=c/a>0 ⇔ (m-3)/m>0; mϵ(-∞,0)∪(3,+∞) (2)
Iz uslova (1) i (2) je skup vrednosti m za koje su rešenja jednačine mx^2-2(m-2)x+m-3=0 istog znaka: mϵ(-∞,0)∪(-3,4].
I sada naprimer ako uzmem neku vrenost manju od 0 , kada to zamenim u jednačinu dobijem rešenja suprotnog znaka, a ne istog, da li neko može da mi kaže gde sam pogrešila???? |
[ lonelyrider_44 @ 18.02.2012. 14:54 ] @
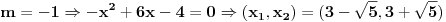 , tj. 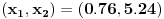 [ cikin @ 18.02.2012. 15:27 ] @
koju vrednost uzimas...mislim da je sve u redu!!!
za -2 i -3 je dobro....
[ cikin @ 12.04.2012. 12:49 ] @
moze ovo samo da mi neko pojasni.... 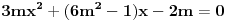 odrediti tako da vece resenje pripada intervalu 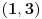 a manje mu ne pripada...dobro sad uradi se 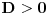 sto odgovara za svako m... e sad mi u zbirci pise da bi 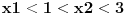 treba da budu ispunjeni uslovi
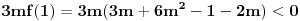 i 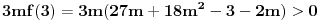 e sad moze neko samo da mi pojasni zasto se mnozi sa ovo 3m i zasto mora da bude manje tj. vece ovo od nule.... [ Nedeljko @ 12.04.2012. 13:10 ] @
Pa, kako je okrenut grafik kvadratne funkcije u zavisnosti od znaka vodećeg člana? (3m)2 je uvek pozitivno, osim u slučaju m=0, koji moraš posebno da ispitaš (onda imaš linearnu jednačinu sa njednistvenim rešenjem, pa se ne može govoriti o tome da je jedinica između rešenja).
[ cikin @ 12.04.2012. 13:46 ] @
shvatio sam zasto 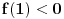 i 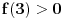 ....vec sto se mnozi sa 3m (da bi prvi clan bio pozitivan??) [ darkosos @ 12.04.2012. 19:44 ] @
Nedeljko ti je vec odgovorio, koeficijent uz kvadratni clan (3m) govori kako je okrenuta parabola, tj gde je + a gde -. Uzmi to kao trik da se prilikom odredjivanja znaka uzme u obzir i taj koeficijent...
[ cikin @ 20.05.2012. 15:34 ] @
evo slican zadatak kao prethodnom, neka su x1 i x2 resenja jednacine 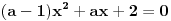 gde je a realan parametar, skup svih vrednosti a za koje su x1 i x2 razliciti brojevi iz intervala (1,2)... e dbr D>0... 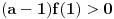 da ne pisem sve, vec ne znam sto se mnozi sa (a-1) [ darkosos @ 20.05.2012. 18:40 ] @
Jes' procitao ti prethodne postove? Kazes da si razumeo zasto je f(1)>0? Mozda si nacrtao parabolu, sa "spicom" nadole, pa video da to znaci da je 1 u zoni van intervala ogranicenog resenjima? Pa probaj da nacrtas i sa "spicom" nagore...
[ cikin @ 20.05.2012. 21:57 ] @
ja tebe ne shvatam uopste, samo mi reci sto se mnozi sa (a-1), pa cu da vidim u cemu je caka....
[ darkosos @ 21.05.2012. 08:53 ] @
Hm, ne znam sad kako da ti napisem, kad je vec napisano nekoliko puta. Ajde samo ti meni reci zasto je f(1) > 0, pa cu ti ja reci zasto se mnozi sa a-1...
[ cikin @ 22.05.2012. 23:46 ] @
pa ovako ako lupam za ovaj drugi primer 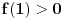 i 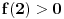 i sad znak je a>0 resenja ce ici izmedju njih i pripadace inervalu, a sad ako su 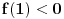 i 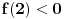 onda treba da je i a<0, jel tako nesto.... [ darkosos @ 23.05.2012. 08:00 ] @
Tako nesto :) tj. bas tako. Inace AB>0 mozes i da tumacis "A i B su istog znaka" (naravno ako se radi o realnim brojevima). A ovde to znaci upravo da 1 i 2 nisu u intervalu (x1,x2), pod pretpostavkom da postoje x1 i x2 i da je x1<x2. Koliko se secam, bas tako nekako se i prica u skoli o grafiku kvadratne funkcije: za tacke van intervala (x1,x2), vrednost funkcije je istog znaka kao i koeficijent uz kvadratni clan, a unutar intervala su vrednosti suprotnog znaka od tog koeficijenta.
Sto ce reci, ako zelimo da je za kvadratnu funkciju f(x)=ax^2+bx+c, neka tacka x0 van intervala (x1,x2), mora biti da su f(x0) i a istog znaka. A to mozemo zapisati i af(x0) > 0.
Da se vratim malo na zadatak. Ako si postavio ove uslove za 1 i 2, to i dalje ne znaci da su x1 i x2 u intervalu (1,2). Moze biti i da je redosled na x-osi: 1,2,x1,x2, dakle i dalje su 1 i 2 van intervala (x1,x2), ali x1 i x2 nisu u (1,2). Ja bih tu dodao uslov jos da je npr. x-koordinata temena parabole (-b/2a) bas u (1,2).
[Ovu poruku je menjao darkosos dana 23.05.2012. u 09:37 GMT+1]
[ cikin @ 24.05.2012. 11:19 ] @
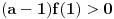 i 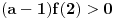 za tacke van intervala (x1,x2), vrednost funkcije je istog znaka kao i koeficijent uz kvadratni clan, a unutar intervala su vrednosti suprotnog znaka od tog koeficijenta( zar ne bi trebalo obratno)...ovo za teme sam shvatio.... [ darkosos @ 24.05.2012. 11:50 ] @
Pa nije, mrzi me da crtam, ali ako je koeficijent u kvadratni clan pozitvan, parabola se "smeje" i raspored znakova je ++++x1---x2++++, dakle izmedju resenja je -, tj. suprotan od pomenutog koeficijenta... I analogno za obrnuto :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|