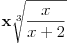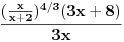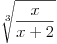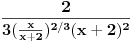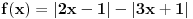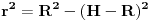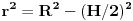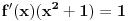kako u wolframalpha da pisem interval odredjenog integrala???

da ne postavljam novu temu( posto se vrv radi preko izvoda) moze neko da pojasni : odrediti najvecu vrednost funkcije

Ne radi se preko izvoda, već preko diskusije apsolutnih vrednosti.

mozes li da uradis....ili da samo pojasnis

Šta je |a|? Kada je a>0, onda je |a|=a, inače je |a|=-a. E, sad lepo zameni a sa onim što se nalazi pod apsolutnom vrednošću, pa izvrši diskusiju. Imaćeš tri slučaja

1. x<-1/3,
2. -1/3<=x<=1/2,
3. x>1/2.

Može i pomoću izvoda: y'=2sgn(2x-1)-3sgn(3x+1). Vidimo da je za x<-1/3 y'>0 (funkcija y raste), za x>=-1/3 y'<0 (funkcija y opada). Jasno je da je tačka maksimuma (-1/3,5/3).

jel moze neko samo da mi kaze kako da iskazem H preko R ako je valjak upisan u sferu i treba odrediti maksimalnu zapreminu... .ja radio ovako : jel ne moze tako....

Nesto ne zvuci bas dobro... Kad napravis presek po osi valjka, dobijas pravougaonik upisan u krug. Naravno, centar kruga je u preseku dijagonala. Pa sad vidi pravougli trougao koji ti treba.

uf ne znam u sta sam gledao... :D ide

Kako da nadjem n-ti izvod funkcije y=arctg(x) ? Hvala.. :D

http://www.math.nthu.edu.tw/~amen/2010/090408-2.pdf, a imas i ovde http://functions.wolfram.com/ElementaryFunctions/ArcTan/20/02/ u jos nekoliko oblika.

Ok, mada je ovo malo komplikovano... Nama je asistent samo dao instrukciju da nadjemo prvi izvod, pa onda imamo , pa to dizem na stepen , s tim sto ne znam da zavrsim zadatak na taj nacin... Jel moze pomoc?


_{[Ovu poruku je menjao devetkamp dana 14.01.2013. u 12:53 GMT+1]}

Mislis na 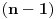izvod, ne na stepen.

Pa verovatno misli na Lajbnizovu formulu za izvod proizvoda funkcija, al nzm koliko ona znaci ovde, jedino ako ga ne zadovoljava i takav odgovor gde ces -ti izvod izraziti preko izvoda nizeg reda (dakle, neka rekurzivna formula).

Al mozes da uradis ovo i drugacije, naime, 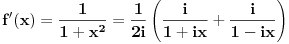, i onda primetis (diferencirajuci ovo dovoljan broj puta da bi bilo ocito) da je .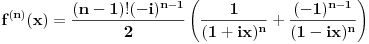
Ili da krenes od 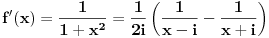, dobices "na oko" lepsu formulu.