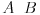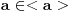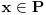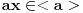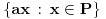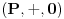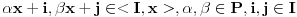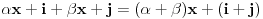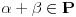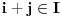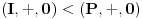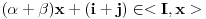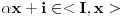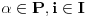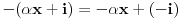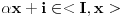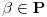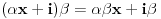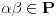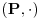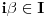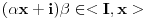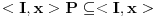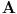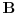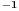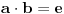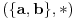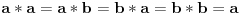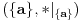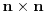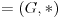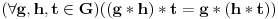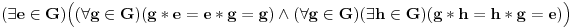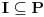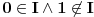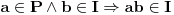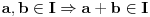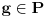|
|
[ Sonec @ 25.02.2012. 21:50 ] @
|
| Neka je 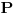 komutativan prsten sa jedinicom i neka je komutativan prsten sa jedinicom i neka je  ideal prstena ideal prstena 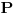 . . 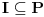 je maksimalan ideal ako je: je maksimalan ideal ako je:
1.  pravi ideal ( pravi ideal (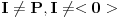 ) )
2. Ako je 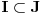 , ,  je ideal prstena je ideal prstena 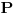 , tada je , tada je 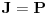 . .
E sad, imamo na primer sledecu teoremu:
Teorema. Neka je 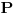 komutativan prsten sa jedinicom i neka je komutativan prsten sa jedinicom i neka je  maksimalan ideal prstena maksimalan ideal prstena 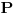 . Tada je . Tada je 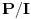 polje. polje.
I sad, u dokazu se koristi sledeci argument:
Neka je 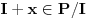 koji je razlicit od nule. Tada vazi koji je razlicit od nule. Tada vazi 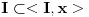 , pa je , pa je 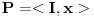
E sada mene zanima, otkud nama da je 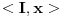 ideal prstena ideal prstena 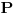 (jer to mora da vazi, ako vazi gornja konstatacija, jer je (jer to mora da vazi, ako vazi gornja konstatacija, jer je  maksimalan ideal). maksimalan ideal).
oznaka: 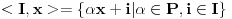
I da, jedno pitanje pored ovoga, ideali se definisu kao podgrupe aditivnog dela prstena (ima jos jedna osobina koju zadovoljavaju, al to me sad ne zanima).
Jel u tom duhu posmatramo sledeci zapis (ovo vazi za glavno idealske domene): 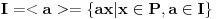 , tj. ideal je generisan sa jednim elementom, al hocu reci, jel se , tj. ideal je generisan sa jednim elementom, al hocu reci, jel se 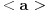 definise ovako jer smo u aditivnoj notraciji? (nisam bio na ovom predavanju, al meni je to zaista logicno, jer da je u pitanju multiplikativna notacija, onda bih znao (kao za ciklcne grupe npr.), a ovde ide ovako jer je aditivna) definise ovako jer smo u aditivnoj notraciji? (nisam bio na ovom predavanju, al meni je to zaista logicno, jer da je u pitanju multiplikativna notacija, onda bih znao (kao za ciklcne grupe npr.), a ovde ide ovako jer je aditivna)
I da, ideale ne moze da definisemo kao podgrupe multiplikativnog dela prstena, jer multiplikativni deo prstena nije grupa?
****offtopic
kako da napisem znak za pravi podskup, ali sa precrtanom crtom, koliko sam izguglao to se postize pomocu naredbe
Code:
\subsetneq
ali za njeno koriscenje mi je potreban paket \amssymb, a koliko vidim on nije dostupan ovde na forumu LINK |
[ Bojan Basic @ 26.02.2012. 01:25 ] @
Citat: Sonec:
****offtopic
kako da napisem znak za pravi podskup, ali sa precrtanom crtom, koliko sam izguglao to se postize pomocu naredbe
Code:
\subsetneq
ali za njeno koriscenje mi je potreban paket \amssymb, a koliko vidim on nije dostupan ovde na forumu LINK
Može, ali se tu nešto komplikuje zbog ovdašnje implementacije LaTeX-a, ne znam ni ja previše tehničkih detalja. Postupa se ovako:
Code:[ tex]
\font\amssy=msbm12
$A\mathrel{\hbox{\amssy\char40}}B$
[/tex]
Rezultat: 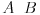 . [ Nedeljko @ 26.02.2012. 07:45 ] @
Citat: Sonec: E sada mene zanima, otkud nama da je 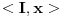 ideal prstena 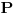 (jer to mora da vazi, ako vazi gornja konstatacija, jer je  maksimalan ideal).
oznaka: 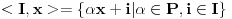
Aksiome ideala se u ovom slučaju dokazuju. Koju aksiomu ne umeš da dokažeš?
Citat: Sonec: Jel u tom duhu posmatramo sledeci zapis (ovo vazi za glavno idealske domene): 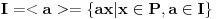 , tj. ideal je generisan sa jednim elementom, al hocu reci, jel se 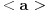 definise ovako jer smo u aditivnoj notraciji? (nisam bio na ovom predavanju, al meni je to zaista logicno, jer da je u pitanju multiplikativna notacija, onda bih znao (kao za ciklcne grupe npr.), a ovde ide ovako jer je aditivna) 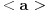 je najmanji ideal koji sadrži  . Dakle, 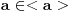 , ali onda za ma koje 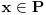 mora da važi 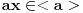 . Obzirom da je 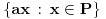 ideal, što se lako proverava, onda je to najmanji ideal koji sadrži  .
Citat: Sonec: I da, ideale ne moze da definisemo kao podgrupe multiplikativnog dela prstena, jer multiplikativni deo prstena nije grupa?
Podgrupe možemo posmatrati u bilo kom monoidu, pa i multiplikativnom monoidu prstena. Međutim, ovako uvedeni ideali su najvažnija podstruktura prstena jer opisuju kongruencije, tj. najvažnije relacije ekvivalencije. [ Sonec @ 27.02.2012. 17:53 ] @
Citat: Nedeljko: Aksiome ideala se u ovom slučaju dokazuju.
1. 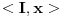 je podgrupa od 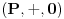
Neka su 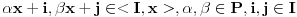 . Tada je 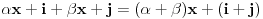 , a 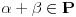 (jer je 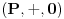 grupa) i 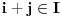 jer je 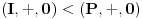 (  je podgrupa grupe  ), to je i 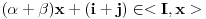
Neka je 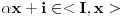 , 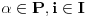 , tada je 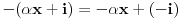 (gde je  inverzna operacija grupe 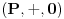 ). Slicnim argumentima dobijamo da 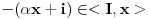 .
Pa dobijamo da je 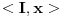 podgrupa grupe 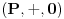 .
2. Ako je 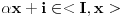 i 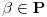 , tada je 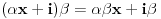 , a kako je 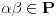 ( 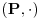 je monoid), a 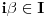 (jer je  ideal), to je i 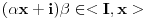 , tj. 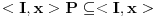
OK?
Citat: Nedeljko: Podgrupe možemo posmatrati u bilo kom monoidu
Jel mozes ovo malo da pojasnis ili da navedes neki primer. Cudno mi je da monoid moze da ima pod grupu.
@Bojan hvala [ Nedeljko @ 27.02.2012. 19:36 ] @
Izvođenje ti je OK. No, šta nije jasno u tome da u nekom podmonoidu monoida svi elementi budu inverzibilni?
[ Sonec @ 27.02.2012. 20:26 ] @
Ako je 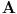 podgrupa grupe 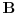 , onda je ujedno i 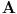 grupa. To vazi, zar ne?

Kako ces da uvedes u podmonoid operaciju za inverz 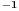 kad ona ne postoji u monoidu. Jer sve operacije iz monoida predstavljaju restrikcije operacija na domen skupa koji je podskup domena monoida. Ili je mozda i neces uvoditi, samo ces reci 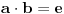 ?
Aj da pitam i ovo, da li moze da podalgebra semigrupe bude grupa? Kako cemo tu, kad nemamo neutralni element?
[ miki069 @ 28.02.2012. 00:15 ] @
Nisam se mnogo udubljivao, jer je teorija, ali ako je komutativni prsten sa jedinicom,
onda i multiplikativna operacija ima neutralni element.
[ Nedeljko @ 28.02.2012. 17:47 ] @
Citat: Sonec: Ako je 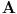 podgrupa grupe 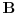 , onda je ujedno i 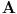 grupa. To vazi, zar ne?

Kako ces da uvedes u podmonoid operaciju za inverz 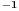 kad ona ne postoji u monoidu. Jer sve operacije iz monoida predstavljaju restrikcije operacija na domen skupa koji je podskup domena monoida. Ili je mozda i neces uvoditi, samo ces reci 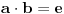 ?
Aj da pitam i ovo, da li moze da podalgebra semigrupe bude grupa? Kako cemo tu, kad nemamo neutralni element?
Grupu možeš da definišeš i samo na jeziku grupoida. [ Sonec @ 28.02.2012. 17:51 ] @
Ajde pokazi. Ali kada je definises, predstavi je i kao n-torku (domen, operacije, konstante, znas vec).
[ Nedeljko @ 28.02.2012. 19:13 ] @
Nema tu šta da se dokazuje. Kao što je monoid polugrupa u kojoj postoji bar jedan element sa osobinom da je neutralan za binarnu operaciju (pri čemu oznaka za njega ne mora da bude u jeziku), tako je i grupa polugrupa u kojoj postoji bar jedan element sa osobinama
1. da je neutralan i
2. da postoji operacija koja je u odnosu na njega operacija invertovanja,
pri čemu nas niko ne bije po ušima da tu operaciju stavljamo u jezik. Takođe, izaberi bilo koju grupu, "zaboravi" šta su neutral i operacija inverza i oni će moći da se rekonstruišu na tačno jedan način.
[ Sonec @ 28.02.2012. 19:59 ] @
Samo mi navedi primer. Preko primera se najlakse uci.
Ako ta operacija, oznaka, sta god, nije u jeziku, gde je onda?
To je malo pokvaren nacin konstruisanja grupe.
[ darkosos @ 28.02.2012. 20:07 ] @
U onome sto tebi treba, nema "menjanja" operacije, zar ne?
[ Nedeljko @ 29.02.2012. 00:14 ] @
U definiciji.
Kao što možeš reći da su neke polugrupe monoidi, a neke nisu. Ili u polugrupi postoji neutralni element ili ne postoji.
[ Sonec @ 29.02.2012. 00:37 ] @
Ajde navedi jednu takvu definiciju. Npr, za grupu, al preko jezika grupoida.
I primer podmonoida monoida kome su svi elementi inverzibilni. Pre bih se zadovoljio sa primerom semigrupe koja ima podalgebru koja je grupa, al bice dovoljno i za monoid samo.
[ Bojan Basic @ 29.02.2012. 00:44 ] @
Citat: Sonec:
Pre bih se zadovoljio sa primerom semigrupe koja ima podalgebru koja je grupa, al bice dovoljno i za monoid samo.
Recimo, polugrupa 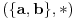 , gde je  definisana sa 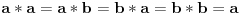 . Tada je podalgebra 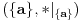 posmatrane polugrupe grupa. [ Sonec @ 29.02.2012. 01:04 ] @
Da, sve ce proci, jeste grupa. Ali grupa sa jednim elementom, poprilicno trivijalna grupa.
Cini mi se da sam negde pre vec video slican primer, i to upravo od tebe Bojane.
Al i dalje bih zeleo da vidim definiciju grupe preko jezika grupoida. (mislim da znam kako bi ona glasila, al sacekacu Nedeljka ili nekoga drugoga da je kaze/ispise)
[ Bojan Basic @ 29.02.2012. 01:29 ] @
Citat: Sonec:
Da, sve ce proci, jeste grupa. Ali grupa sa jednim elementom, poprilicno trivijalna grupa.
Napravi sam koliko god velik primer hoćeš: prosto namontiraj tako da ti u jednom ćošku bude kvadrat 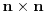 koji je grupa, a ostatak tablice popuni kako god želiš, pazeći jedino na asocijativnost (jedna mogućnost: popuni čitav ostatak tablice jednim te istim elementom).
Citat: Sonec:
Al i dalje bih zeleo da vidim definiciju grupe preko jezika grupoida. (mislim da znam kako bi ona glasila, al sacekacu Nedeljka ili nekoga drugoga da je kaze/ispise)
Ja moram priznati da i dalje ne vidim gde zapinješ. No dobro, evo definicije.
Grupoid 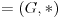 je grupa akko 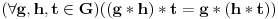 i 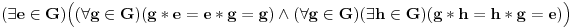 .
Da li se možda nešto ne razumemo? [ Sonec @ 29.02.2012. 09:24 ] @
Da, tako sam i mislio.
Al ne svidja mi se taj nacin kako god da okrenes, no, to je moja stvar.
[ miki069 @ 30.04.2018. 12:50 ] @
Podskup skupa svih polinoma sa osobinom da je p(1) = 0 je ideal prstena polinoma (P, +, *).
Da li je glavni ideal?
Ako gledam aditivnu operaciju, onda nije.
Ako gledam multiplikativnu operaciju, onda jeste, jer je generator ideala polinom x-1.
Mislim da jeste, ali bih voleo da otklonim neodumicu.
[ Nedeljko @ 30.04.2018. 15:44 ] @
Ideal komutativnog prstena  sa jedinicom je skup 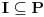 koji ima osobine:
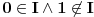 ,
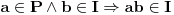 ,
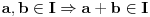 .
Ideal  komutativnog prstena  je glavni ako postoji 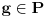 takav da je 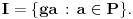
Odgovor na tvoje pitanje je potvrdan. [ miki069 @ 01.05.2018. 15:58 ] @
Hvala Nedeljko.
[ Nedeljko @ 01.05.2018. 20:55 ] @
Prsten polinoma nad poljem je glavnoidealski prsten, tako da je svaki njegov ideal glavni.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|
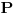 komutativan prsten sa jedinicom i neka je
komutativan prsten sa jedinicom i neka je  ideal prstena
ideal prstena 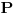 .
. 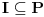 je maksimalan ideal ako je:
je maksimalan ideal ako je: pravi ideal (
pravi ideal (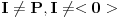 )
)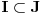 ,
,  je ideal prstena
je ideal prstena 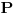 , tada je
, tada je 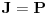 .
.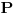 komutativan prsten sa jedinicom i neka je
komutativan prsten sa jedinicom i neka je  maksimalan ideal prstena
maksimalan ideal prstena 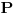 . Tada je
. Tada je 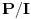 polje.
polje.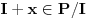 koji je razlicit od nule. Tada vazi
koji je razlicit od nule. Tada vazi 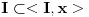 , pa je
, pa je 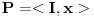
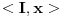 ideal prstena
ideal prstena 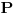 (jer to mora da vazi, ako vazi gornja konstatacija, jer je
(jer to mora da vazi, ako vazi gornja konstatacija, jer je  maksimalan ideal).
maksimalan ideal).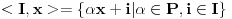
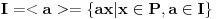 , tj. ideal je generisan sa jednim elementom, al hocu reci, jel se
, tj. ideal je generisan sa jednim elementom, al hocu reci, jel se 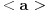 definise ovako jer smo u aditivnoj notraciji? (nisam bio na ovom predavanju, al meni je to zaista logicno, jer da je u pitanju multiplikativna notacija, onda bih znao (kao za ciklcne grupe npr.), a ovde ide ovako jer je aditivna)
definise ovako jer smo u aditivnoj notraciji? (nisam bio na ovom predavanju, al meni je to zaista logicno, jer da je u pitanju multiplikativna notacija, onda bih znao (kao za ciklcne grupe npr.), a ovde ide ovako jer je aditivna)