. Posto onda je i . Kako je normalan i na i na to je onda .
Znas da je , pa odatle nadji . Takodje, kako imas da tacka . Nadjes vektor normale ravni , imas tacku koja pripada ravni, i onda lako nadjes jednacinu ravni.

Znaci: ; tj. ?


A kako da nadjem ovu simetricnu tacku (sledeci deo zadatka)?

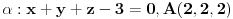
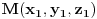
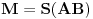
Nadjes tacku koja predstavlja projekciju tacke na ravan . Tada vazi da je ( je srediste duzi ).
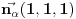
Vektor normale ravni je . Neka je prava koja sadrzi tacke i . Tada vazi
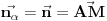
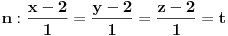
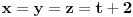
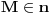
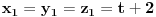
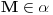
Jednacina normale koja prolazi kroz je , tj. . Kako to vazi , a sa druge strane , pa vratis ovo u jednacinu ravni i nadjes .
Kad nadjes onda nadjes i tacku , a posle lako nadjes tacku .

Nzm dal ti je tacno, nisam racunao.

Ako sam dobro razumeo vracam u jednacinu ravni i dobijam da je , i odatle imam da je tacka ?


I opet mi nije jasno kako se dolazi do tacke B...

Tacka je srediste duzi , tj. ako je i tada je . Ti imas , i imas , i sad nadji .

Ajde molim te pokazi mi na konkretnom primeru za prvu koordinatu (Xb) kako se dolazi do nje? Sa cime treba da je izjednacim?

Iz nalazis
Iz nalazis

I odatle nadjes

I ispada da je B(0,0,0)?

Da.

Provera:




sve je u redu

Obavezno uradi zadatak: Naći tačku simetričnu tački A u odnosu na pravu p.
I ta verzija često pada na ispitima.

Uputstvo:
Nemoj da projekciju tačke A na pravu p tražiš kao presek prave p i prave n.
Prava n je normalne na pravu p i sadrži tačku A.
Pomučićeš se oko vektora prave n, jer ćeš morati da koristiš i uslov da se dve prave seku i da se seku pod pravim uglom.

Projekciju tačke A na pravu p traži kao presek prave p i ravni Pi.
Ravan Pi je normalna na pravu p i sadrži tačku A.
Njen vektor odmah imaš, jer je to vektor prave p.

Najbolje uradi zadatak na oba načina.
Prvo preko ravni, a onda preko prave.
Videćeš koja je razlika u dužini zadatka.