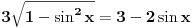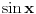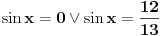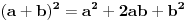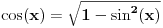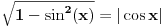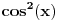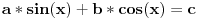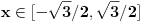Prosta jednacina :)

[ Nepoznat covek @ 05.03.2012. 15:20 ] @

Jednacina glasi ovako: 2sin(x) + 3cos(x) = 3 (Nadam se da se ne ljutite sto pisem ovako, ali ne znam kako vi postavljate ovo u obliku slika, msm. koji sajt ili skriptu za to koristite :) )

Znaci, krenem sa uvodjenjem zamene:
cos x = √(1 − sin² x)

2sin x + 3cos x = 3
2sin x + 3√(1 − sin² x) = 3.

Zamenim umesto p = sin(x)

2p + 3√(1 − p²) = 3 Jednacina (1) - Kvadrira se, to vidim, da se otarasim korena..

E sad, otkud ovde ovo "12p√(1 − p²)"? Sve ostalo je prosto i jasno..

4p² + 12p√(1 − p²) + 9(1 − p²) = 9
12p√(1 − p²) − 5p² = 0
√(1 − p²) = 5p / 12

Dobro, zamenim u jednacinu (1),

2p + 3(5p / 12) = 3
2p + 5p / 4 = 3

Kad se resi,

p = 12/13

sin x = 12/13
cos x = √(1 − (12/13)²) = 5/13

[ lonelyrider_44 @ 05.03.2012. 16:11 ] @

Koren ostavljas sam sa leve strane,

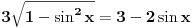
, pa tek onda kvadriraš. Smena može i ne mora. Dalje rešavaš kvadratnu jednačinu, rešenja za

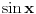
su:

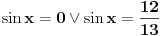
[ darkosos @ 05.03.2012. 17:18 ] @

Citat:

Nepoznat covek:E sad, otkud ovde ovo "12p√(1 − p²)"? Sve ostalo je prosto i jasno..

To je srednji clan kvadrata binoma

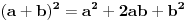
[ Nedeljko @ 05.03.2012. 17:37 ] @

Najpre, u opštem slučaju jednakost

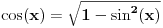
NIJE TAČNA!

Tačno je

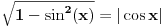
i o tome se MORA voditi računa.

[ Nepoznat covek @ 05.03.2012. 17:58 ] @

Ljudi, hvala svima na tako brzim odgovorima, ok, vodicu racuna o apsolutnoj vrednosti, hvala :)
btw. uradih ga preko:

- Iz prve izracunam cos(x)= (3-2sin(x))/3), pa uvrstio u..

- sin^2(x)+cos^2(x)=1, posle kvadratna jednacina, nikakva mudrost, to je to, hvala svima jos jednom.. :)

[ cikin @ 05.03.2012. 18:25 ] @

mozes sve kvadriras, pa delis sa

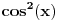
...pa resis kvadratnu po tgx

[ darkosos @ 05.03.2012. 20:26 ] @

Citat:

Nepoznat covek:
- Iz prve izracunam cos(x)= (3-2sin(x))/3), pa uvrstio u..
- sin^2(x)+cos^2(x)=1, posle kvadratna jednacina

Obrati paznju da na taj nacin mozes dobiti resenja koja nisu resenja sitema, tj. ne zadovoljavaju linearnu jednacinu. Ima vec takvih primera ovde, skoro je bilo...

[ miki069 @ 05.03.2012. 23:52 ] @

Jednačinu oblika:

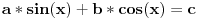
Deliš sa

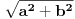
Kako dalje i tri urađena primera imaš na:
https://www.elitesecurity.org/t403869-Trigonometrijska-jednacina

[ cikin @ 23.03.2012. 18:15 ] @

znam da nije mesto, al da ne pravim novu temu.... evo ovako u zbirci pise resenje koje sam i ja dobio

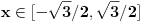
i da x nije 0.....e sad wolfram mi je izbacilo da x moze da ide do -1 http://www.wolframalpha.com/in...x%5E2%29%29%2Fx%3C%3D1%2Fsqrt3 a ako zamenim ispadne da moze, pa ako moze neko samo za taj deo da mi pomogne....

[ darkosos @ 23.03.2012. 19:13 ] @

Nejednacina je ispunjena za sve x za koje je leva strana negativna. Posto 1-x^2 s' jedne strane mora biti pozitivno, a sa druge strane uvek je manje od 1, imamo da je leva strana manja od nule za sve negativne x za koje je 1-x^2 pozitivno, tj [-1,0)