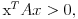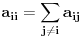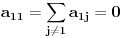[ onako @ 06.03.2012. 15:24 ] @
|
[ Nedeljko @ 06.03.2012. 17:35 ] @
Tvoja kvadratna forma je ništa drugo do
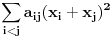 . .Ako je red matrice jednak 1, onda tvrđenje ne važi jer se za nenula vektor dobija nula. Ako je red matrice jednak 2, onda tvoje tvrđenje ne važi, jer se za vektor (1,-1) dobija nula. Ako je red matrice veći od 2, onda je tvrđenje tačno, jer iz 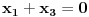 i i 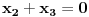 sledi sledi 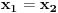 , a onda iz , a onda iz 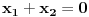 sledi sledi 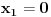 itd. itd.[ darkosos @ 06.03.2012. 20:19 ] @
Zar se za red 1 ne dobija ax^2?
[ Nedeljko @ 06.03.2012. 22:54 ] @
Ne, jer je suma ničega (ostalog u vrsti/koloni) nula.
[ darkosos @ 07.03.2012. 07:33 ] @
To je ako gledas sumu; ali nisam siguran da ta suma dobro predstavlja posmatrani proizvod vektora i matrice za slucaj n=1; matrica je [a] a vektor [x]...
Uostalom, mozda nije doreceno u postavci kako to izgleda za n=1... [ Nedeljko @ 07.03.2012. 11:02 ] @
[ darkosos @ 07.03.2012. 11:45 ] @
Citat: onako: Data je simetricna matrica u kojoj su svi elementi pozitivni, a_{ij}>0, a elementi na diagonali su sumacija van-diagonalnih elemenenata u odgovarajucem redu ili koloni (jer je matrica simetricna): npr. drugi elemenat diagonale jednak je sumaciji ostalih elemenata u drugom redu (ili drugoj koloni). Po meni, ovo nije definisano kada je n=1; interesantno pitanje, svakako :) Da li je 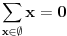 ? ?Ja sam blizi tome da to nije definisano, tj. da je potreban dogovor. U ovom konkretnom slucaju, implicitno se podrazumeva da postoje elementi van dijagonale, tj da je n>1; mislim da bi to trebalo da se posebno tretira u postavci. Jer formalizacija koju si ti dao je sira od ovakve postavke. [ onako @ 07.03.2012. 16:59 ] @
Upravo tako, n>2.
Argument o tumacenju kvadratne forme kao sumacije je sve sto je bilo potrebno. Hvala. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|