Kako misliš da rešenje bude nešto što je data (matrica B)?

Meni izgleda da da... Pitanje se svodi na to, ako sam dobro razumeo, da ako B minimizira da li onda minimizira i ?
Posto je kvadriranje rastuca funkcija za x>0, onda imas za g(X)=||A-X|| i f(x)=x^2, da ako je B minimum funkcije g, da je onda B minimum i funkcije fog...
Slicno bi trebalo da vazi i za ovaj drugi primer.

@Nedeljko: zbog toga sledi, "i poznato je..."

@darkosos: imam slicno rezonovanje. No, cudi me da u literaturi cesto srecem drugacije oblike, a resenje za
minimum bi trebalo biti identicno. Pretpostavljam da se radi o specificnoj aplikaciji/polju.

Mozda je pitanje do toga kako to efektivno izracunati, pa se daju razni oblici koji se lakse ili teze racunaju...

Čekaj, A i B su date matrice, tj. konstantne, pa je samim tim ||A-B|| konstanta. Kako misliš da nešto minimizira konstantu?

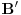
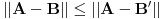
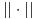
Da li se pitanje odnosi na ovo: Date su matrice i takve da za ma koju matricu važi , gde je Frobeniusova norma. Ako uzmemo neku srodnu formu kao što je neka od navedenih, da li onda imamo iste minimume ( je fiksirano).

Odgovor je "da" upravo iz razloga koji je darkosos naveo.

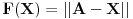
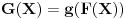
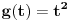
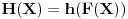
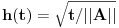
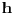
Ti tapravo minimizuješ nelinearne funkcionale , za i za . Odgovor je potvrdan zato što su funkcije i monotono rastuće.

Upravo tako, izvinjavam se ako sam pogresno postavio problem.
Interesovalo me je da li je resenje B koje je minimum prve, je ustvari i resenje bilo koje druge norme
koja je monotona transformacije ove prve.

_{[Ovu poruku je menjao onako dana 09.03.2012. u 18:03 GMT+1]}