[ Nepoznat covek @ 10.03.2012. 18:21 ] @
| Naći ostatak dijeljenja broja 1234^1234 sa 11. Na kom principu se rade ovi zadatci.. Niti mogu da napišem 1234, kao 11 na neki stepen, niti.. |
|
[ Nepoznat covek @ 10.03.2012. 18:21 ] @
[ Picsel @ 10.03.2012. 18:50 ] @
[ Sonec @ 10.03.2012. 20:19 ] @
Citat: Picsel: Moze ovako - po maloj Fermaovoj teoremi 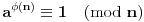 . . Samo jedna mala ispravka, ovo je Ojlerova teorema, a posledica Ojlerove tereme je Mala Fermaova teorema za 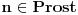 ( ( je prost broj). je prost broj).Inace, funkcija 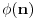 (poznatija i kao Ojlerova funkcija, negde se zapisuje i kao (poznatija i kao Ojlerova funkcija, negde se zapisuje i kao  ) nam govori koliko ima brojeva izmedju (ukljucujuci) ) nam govori koliko ima brojeva izmedju (ukljucujuci) i i  koji su uzajamno prosti sa koji su uzajamno prosti sa  . Pa se zbog toga moze reci da je . Pa se zbog toga moze reci da je 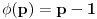 gde je gde je  prost broj. A samim tim se moze reci da je prost broj. A samim tim se moze reci da je 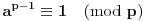 (sto i predstavlja Malu Fermaovu teoremu, uz uslov da je i (sto i predstavlja Malu Fermaovu teoremu, uz uslov da je i 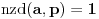 ). ).Takodje (ne skodi malo informacija) Ojlerova funkcija predstavlja red Ojlerove grupe 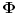 ( (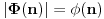 ), gde je: ), gde je: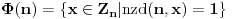 Na primer, 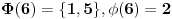 . .[ darkosos @ 10.03.2012. 20:54 ] @
Ajd' i ja da dodam jos nesto malo, "sa druge strane", hocu recu jedan osnovnoskolski rezon... Posto sam i sam zaboravio na ovu teoremu (ako sam je ikad i znao :), krenuo sam ovako:
prvo sam redukovao 1234 na 2 (mod 11). Zatim sam, naoruzan strpljenjem trazio stepene dvojke (mod 11) verujuci da ce negde poceti da se ponavljaju: 2 4 8 5 10 9 7 3 6 1 2 i eto, desilo se posle 10og stepena... E sad zasto je bas 10 i zasto su samim tim svi ostaci razliciti, to je za one koji hoce vise :) a moze dovesti do same navedene teoreme. Elem, sada jos ostaje da se, koristeci 1234=10*123+4 zakljuci da dati broj ima isti ostatak posle deljenja sa 11 kao i broj 2^4=16. a to je 5. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|