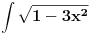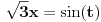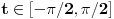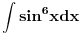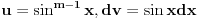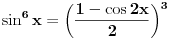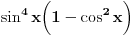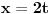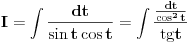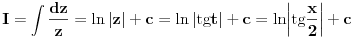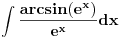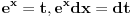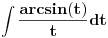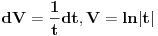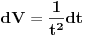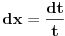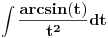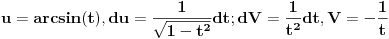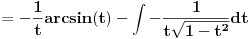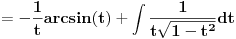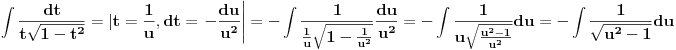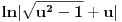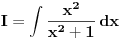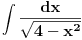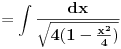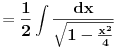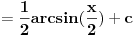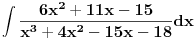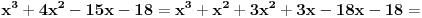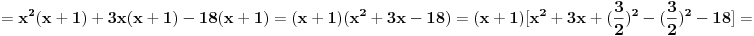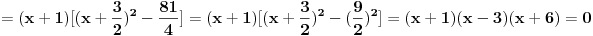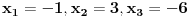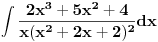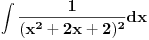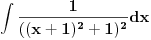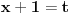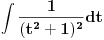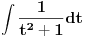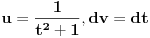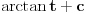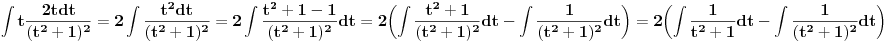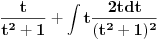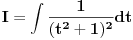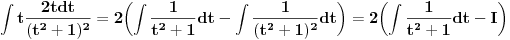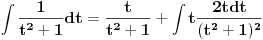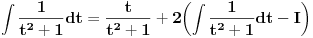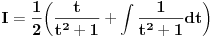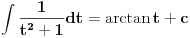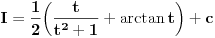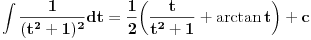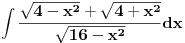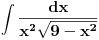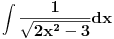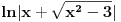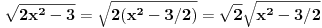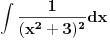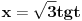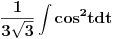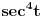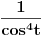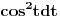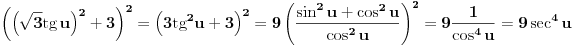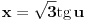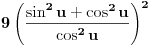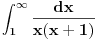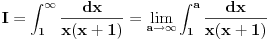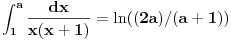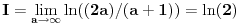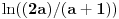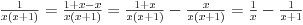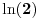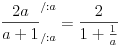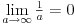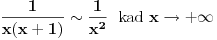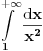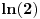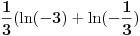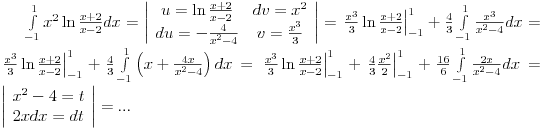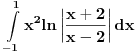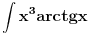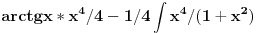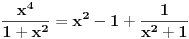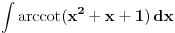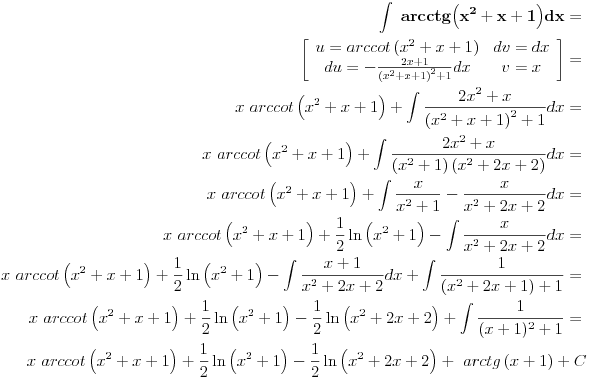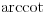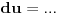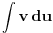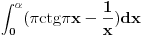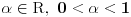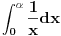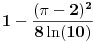[ patkan1992 @ 21.03.2012. 16:12 ] @
|
[ patkan1992 @ 23.03.2012. 21:37 ] @
[ Sonec @ 23.03.2012. 22:14 ] @
[ Sonec @ 23.03.2012. 23:17 ] @
[ patkan1992 @ 26.03.2012. 15:36 ] @
[ miki069 @ 26.03.2012. 20:30 ] @
Poslednji se rešava smenom u=1/t
Batali taj Wolframalpha, jer te on samo još više zbunjuje. [ Sonec @ 26.03.2012. 21:01 ] @
Probaj smenom koju je miki predlozio.
[ patkan1992 @ 26.03.2012. 21:17 ] @
A sta sa korenom da radim?
Ne razumem ovaj... [Ovu poruku je menjao patkan1992 dana 26.03.2012. u 22:47 GMT+1] [ SrdjanR271 @ 26.03.2012. 22:29 ] @
[ patkan1992 @ 26.03.2012. 23:04 ] @
[ different @ 27.03.2012. 14:42 ] @
Patkan1992,
evo cio zadatak na linku: http://matematika.ba/component...ntegral-parcijalna-integracija [ Nedeljko @ 02.04.2012. 18:17 ] @
Nije. Ti u poslednje koraku uvodiš smenu x/2=t, ali onda moraš da smeniš i dx sa 2dt.
[ patkan1992 @ 02.04.2012. 19:54 ] @
[ darkosos @ 02.04.2012. 20:23 ] @
Das nekom da ti uradi :) ili bacis kocku...
[ patkan1992 @ 02.04.2012. 20:58 ] @
Ozbiljno nema? Neka formulica ili slicno?
[ darkosos @ 02.04.2012. 21:23 ] @
Ima formulica http://en.wikipedia.org/wiki/C...ction#General_formula_of_roots mada meni izgleda strasno :)
[ patkan1992 @ 02.04.2012. 21:47 ] @
Haha, neka hvala sto se ovoga tice. :) Ako neko zna laksi nacin, voljan sam da ga naucim :))
[ Sonec @ 02.04.2012. 21:50 ] @
Ne vidim u cemu je problem, neces ti dobiti kao nulu neki razlomak i slicno (mozes, al to se ne daje u principu), obicno je to 1,-1,2,-2,3,-3 i to je to. Posle kad smanjis za jedan stepen lakse ces naci ostale nule. Ne fali ti nista da malo racunas.
[ darkosos @ 03.04.2012. 12:45 ] @
Ovi mladi danas bi sve na brzinu i odma' ... niko bre nece motiku u ruke :)
[ Nedeljko @ 03.04.2012. 21:05 ] @
Lepo je kad se neko snađe, ali reci iskreno, da li si ovo znao da uradiš dok nisi znao rešenja ili tek na osnovu poznatih rešenja?
[ petarm @ 04.04.2012. 07:45 ] @
Probao sam. Nisam znao resenja. Ovi ovakvi fazoni se koriste u 1. razredu gimnazije dok se jos ne radi Bezuova teorema ni Hornerova sema. Dosta sam se igrao s ovim ranije. Jugoslav Jankov u svojoj zbirci za 1. razred gimnazije ima dosta ovih igrarija. Krene od jednostavnijih slucajeva:
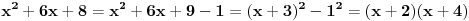 Daje takvih more primera. A ovaj prvi deo sam video ranije u takmicarskoj zbirci gde je bio dat polinom desetog stepena. Ali se vrlo lako grupisao na isti ovaj nacin. Ne znam napamet kako izgleda taj primer, ali mislim da znam u kojoj se zbirci nalazi pa cu ga napisati. [ Nepoznat covek @ 05.04.2012. 18:20 ] @
Uh, i mi smo počeli integrale u školi. Biće ovo zanimljivo. Pitaj šta imaš, pomoćiću šta znam
[ patkan1992 @ 08.04.2012. 14:35 ] @
[ Sonec @ 08.04.2012. 15:03 ] @
[ SrdjanR271 @ 08.04.2012. 15:07 ] @
Prvo smena x+1=t, pa posle t=tg(u) ili rekurentna formula.
Edit: Sonec bio brzi :) [ patkan1992 @ 08.04.2012. 15:39 ] @
Malo si me zbunio Sonec sada. :) Uradio sam parcijalnu (2 puta). Kod prve imam da je
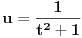 , , 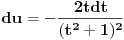 , , 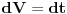 , , 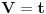 . .Sada imam: 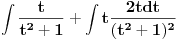 Opet parcijalna: 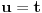 , , 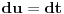 , , 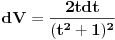 , , 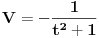 I imam: 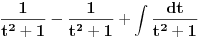 , sto je isto sto i , sto je isto sto i 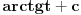 Gde mi je ovde 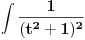 ? ?Gledam sada ponovo ovo sto sam radio i jedino da ga izvucem odavde: 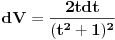 ? Je l' si na to ciljao? ? Je l' si na to ciljao?EDIT: Srdjane, to sto si ti napisao mi se cini komplikovanije :) Uzgred, sta je "rekurentna formula"? [ Sonec @ 08.04.2012. 15:51 ] @
[ patkan1992 @ 08.04.2012. 16:05 ] @
Ne razumem koje je resenje... Pokusavam da provalim, al' jok. Poredim sa Wolframalpha resenjem i ne ide mi u glavu kako iz ovog sto si ti napisao nastaje ono na njihovom sajtu.
Vidim da treba bez 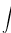 , greskom sam slucajno stavio i integral. , greskom sam slucajno stavio i integral.EDIT: Shvatio sam, ali opet imam mali problem. Dobijam: 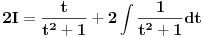 , i to je , i to je 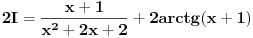 Ova dvojka sa 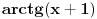 tu ne treba da bude... U kom koraku je trebalo da nestane ona? tu ne treba da bude... U kom koraku je trebalo da nestane ona?[Ovu poruku je menjao patkan1992 dana 08.04.2012. u 17:17 GMT+1] [Ovu poruku je menjao patkan1992 dana 08.04.2012. u 17:20 GMT+1] [ Sonec @ 08.04.2012. 16:29 ] @
[ patkan1992 @ 08.04.2012. 16:37 ] @
Vidim gde sam zeznuo! Hvala puno :)
[ patkan1992 @ 23.04.2012. 16:22 ] @
Poceo sam da vezbam za kolokvijum, i buni me sada ovo:
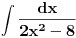 Radim ga ovako: 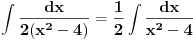 E sad, izvukao sam ovu 4 iz imenioca i ostaje mi: 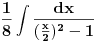 Ako je poslednji korak uopste dobar, sta sledece treba da radim ovde? Vidim da u prethodnom koraku imenilac moze da se rastavi na 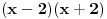 , pa da se radi preko racionalne, ali ima li neki drugi nacin koji ne vidim? , pa da se radi preko racionalne, ali ima li neki drugi nacin koji ne vidim?[ miki069 @ 23.04.2012. 16:34 ] @
Treba preko "racionalne".
(X-2)*(X+2) Ako posle 2 meseca "vežbanja" integrala po Wolframu i forumima, ne znaš da uradiš ovaj zadatak, slučaj je alarmantan. Prijateljski saveti: 1. Batali Wolfram 2. Ponovi komletno polinome. 3. Ponovi kompletno trigonometriju. 4. Ponovi kompletno izvode. 5. Tablični integrali. 6. Metoda smene. ... 22. Uzmi neki privatan čas. Sa ovog Foruma ti preporučujem Nedeljka ili Soneca. [Ovu poruku je menjao miki069 dana 23.04.2012. u 17:45 GMT+1] [ Nepoznat covek @ 23.04.2012. 17:04 ] @
To ti je kad izvučeš minus tj. obrneš mesta
Tablica integrala .. Imaš na jt, mene su oduševili, rajak škola, sve lepo objašnjeno Rajak, jt kanal.. imaš pri dnu.. Slažem se s ljudima, batali se volframa i venea u šake! Ili bilo koju zbirku, pa ošini po polinomima i ostalom.. [ Nepoznat covek @ 23.04.2012. 18:37 ] @
Možda da rastaviš integral na 2 dela, pa svaki radi posebno. Mogu onda koreni da se ujedine, biće ti lakše..
[ darkosos @ 23.04.2012. 19:03 ] @
Nisam ni u kakvoj formi za integrale, ali nekako mi izgleda previse komplikovano, uzimajuci u obzir i sta kaze wolfram. Da nije dole cetvrti stepen?
[ Nepoznat covek @ 23.04.2012. 19:23 ] @
Stvarno, moguće da je dole 4-ti stepen, umnogome bi ti uprostilo stvari..
[ patkan1992 @ 23.04.2012. 23:18 ] @
Ups, i jeste cetvrti stepen. Umem sad ovo da resim. :)
[ darkosos @ 25.04.2012. 12:43 ] @
Probaj x = 1/t
[ Nedeljko @ 25.04.2012. 13:31 ] @
Može trigonometrijskim smenama, hiperboličkim smenama ili Ojlerovim smenama.
[ SrdjanR271 @ 25.04.2012. 13:50 ] @
Najlakse ti je ovo x=1/t, kao sto Miki rece.
Posle imas samo 9t^2-1=u^2. [ patkan1992 @ 25.04.2012. 20:45 ] @
[ Sonec @ 25.04.2012. 21:24 ] @
Nemoj ovakve integrale da ucis kao tablicne. Umesto toga, nauci kako se oni resavaju. Hocu reci, npr.
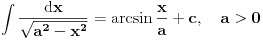 , al ti ne moras da ucis to napamet *, dovoljno je da znas da se ovakav integral resavava smenom , al ti ne moras da ucis to napamet *, dovoljno je da znas da se ovakav integral resavava smenom 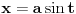 . .Slicno i ovde, ti znas za formulu 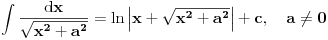 , umesto toga, naucis kojom metodom se ovaj integral moze resiti (na primer, , umesto toga, naucis kojom metodom se ovaj integral moze resiti (na primer, 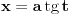 ), i onda to primenjujes na opste slucajeve. Ovo ucenje napamet i pozivanje na tablicne integrale mi se uopste ne svidja. To je prolazno znanje (al sad, ja ne znam koliko ce ti to trebati u zivotu). ), i onda to primenjujes na opste slucajeve. Ovo ucenje napamet i pozivanje na tablicne integrale mi se uopste ne svidja. To je prolazno znanje (al sad, ja ne znam koliko ce ti to trebati u zivotu).*a mozda vam daju da koristite tablice integrala na ispitu, onda ovo pada u vodu (sem ako ne zelis za svoju dusu da naucis) [ patkan1992 @ 25.04.2012. 21:55 ] @
[ SrdjanR271 @ 25.04.2012. 22:39 ] @
Kolko ja vidim tebi je x^2+3 a u wolframu x^2+1
[ patkan1992 @ 25.04.2012. 22:43 ] @
Evo ga sada, ispravio sam :)
[ patkan1992 @ 25.04.2012. 22:51 ] @
[ Nedeljko @ 25.04.2012. 23:29 ] @
Do sada si već 10x mogao da naučiš integrale da si radio po nekoj klasičnoj dobroj zbirci. Bataljuj volfram. Klasika je davala bolje rezultate.
[ anonimnistefi @ 27.04.2012. 09:12 ] @
Nedeljko,jel znas neku dobru zbirku integrala?
[ Nedeljko @ 09.05.2012. 19:14 ] @
Hajde, potrudi se da izračunaš određeni integral iz drugog reda, pa ako ti ne bude išlo, pomoći ću ti.
[ patkan1992 @ 09.05.2012. 23:24 ] @
[ Nedeljko @ 10.05.2012. 00:09 ] @
Patkane, ovo je integral racionalne funkcije.
Kako se radi? Imaš integral 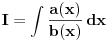 . .1. Izračunaš NZD od brojioca i imenioca, pa ako dobiješ nešto stepena najmanje jedan, skratiš sa tim. Time je problem sveden na slučaj integrala količnika uzajamno prostih polinoma. Stoga ćemo nadalje pretpostaviti da su 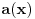 i i 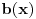 uzajamno prosti polinomi. uzajamno prosti polinomi.2. Podeliš euklidski brojilac sa imeniocem. Dakle, neka je 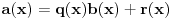 , gde je , gde je 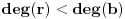 . U tom slučaju je . U tom slučaju je 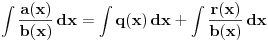 . Integral polinoma pretpostavljam da znaš da računaš (sabirak po sabirak). Time je problem sveden na računanje integrala količnika uzajamno prostih polinoma, gde je deljenik manjeg stepena od delioca. . Integral polinoma pretpostavljam da znaš da računaš (sabirak po sabirak). Time je problem sveden na računanje integrala količnika uzajamno prostih polinoma, gde je deljenik manjeg stepena od delioca.3. Rastaviš delilac na proste činioce. Dakle, 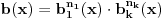 , gde su , gde su  prosti i uzajamno prosti polinomi stepena bar jedan. prosti i uzajamno prosti polinomi stepena bar jedan.4. Predstaviš racionalnu funkciju kao zbir sabiraka sa neodređenim koeficijentima na sledeći način: Činiocu 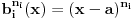 odgovara niz sabiraka odgovara niz sabiraka 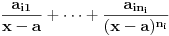 , a činiocu , a činiocu 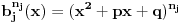 , gde je , gde je 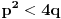 niz sabiraka niz sabiraka 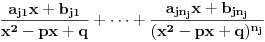 . .5. Kad si to tako rastavio, onda odrediš neodređene koeficijente u brojiocima tako što obe strane pomnožiš sa imeniocem, pa izmnožiš sve i izjednačiš koeficijente uz iste stepene i dobićeš sistem linearnih jednačina po neodređenim koeficijentima sa jedinstvenim rešenjem. 6. Na kraju integrališ sve jedno po jedno. Imaj u vidu smenu 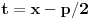 kod imenioca koji su stepeni od kod imenioca koji su stepeni od 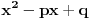 . Takođe, integral . Takođe, integral 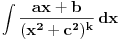 se smenom se smenom 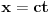 svodi na integral oblika svodi na integral oblika 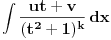 . Dalje je . Dalje je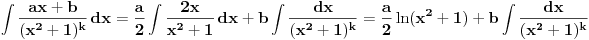 . .Kako na kraju integraliti 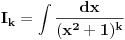 za za 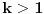 ? Parcijalnom integracijom dobijamo da je ? Parcijalnom integracijom dobijamo da je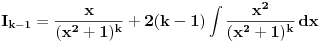 , ,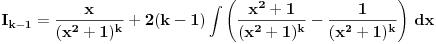 , ,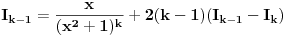 , ,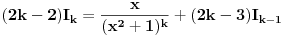 , ,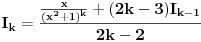 . .[ Sonec @ 10.05.2012. 08:49 ] @
[ patkan1992 @ 10.05.2012. 13:27 ] @
[ patkan1992 @ 10.05.2012. 14:47 ] @
[ igorpet @ 10.05.2012. 14:57 ] @
Imam ja jedno pitanje za tebe.
Da li postoji logaritam za negativne vrednosti? Kako stojis sa pravilima za logaritmovanje? 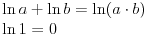 [Ovu poruku je menjao igorpet dana 10.05.2012. u 16:32 GMT+1] [Ovu poruku je menjao igorpet dana 10.05.2012. u 16:32 GMT+1] [Ovu poruku je menjao igorpet dana 10.05.2012. u 16:33 GMT+1] [ patkan1992 @ 10.05.2012. 16:21 ] @
[ igorpet @ 10.05.2012. 17:06 ] @
Citat: Ovo sto si dobio (uslovno) moze da se uprosti ovako: 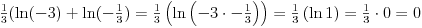 Citat: patkan1992: Vidim rezultat na wolframu da je 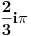 , toliko dobijem i ja... , toliko dobijem i ja...E sad, ovo tvoje resenje, koliko ja vidim, ne moze da bude 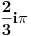 pa mi nije jasno kako to dobijes i ti? pa mi nije jasno kako to dobijes i ti?[Ovu poruku je menjao igorpet dana 10.05.2012. u 18:16 GMT+1] [ patkan1992 @ 10.05.2012. 17:39 ] @
[ igorpet @ 10.05.2012. 18:42 ] @
Citat: patkan1992: Onda wolfram gresi? Nije mi jasno, zato i pitam. Imam 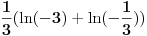 . .Ovo u zagradi je (po wolframu) 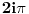 , sto mu iz gornjeg izraza dodje jednako , sto mu iz gornjeg izraza dodje jednako 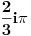 . .Uradi ponovo zadatak. Pre ce biti da si ti negde pogresio. Postavi i resenje da vidimo kako si ga resio. [ Nedeljko @ 10.05.2012. 18:59 ] @
Patkane, ako radiš realnu analizu, onda logaritam postoji samo od pozitivnih brojeva. Ako radiš kompleksnu, onda moraš da izdvojiš jednu granu logaritma i da napišeš na koju se zadatak odnosi. Nije poenta da se samo napiše nešto bez značenja.
[ patkan1992 @ 10.05.2012. 19:00 ] @
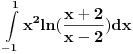 Sada preko parcijalne: 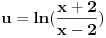 ; du = ; du = 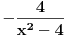 ; ; 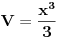 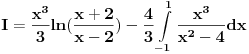 Sada ovaj integral iznad resavao smenom 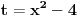 , odatle promenio granice , odatle promenio granice  , i on ispada jednak nuli. , i on ispada jednak nuli.Ostaje samo da se zamene granice 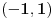 na ovo na ovo 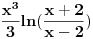 , i tu dobijam ono sto sam vec napisao u prethodnom postu. , i tu dobijam ono sto sam vec napisao u prethodnom postu.P.S. Nedeljko, asistentkinja je dala ovaj zadatak za domaci, malo je i meni cudno da ispadaju ovakvi logaritmi posto ih nikada nismo radili. Vidim da mi se resenje poklapa sa wolframom, pa ne znam sta se desava... Nije mi jasno. Eto gore kako sam radio, pa ako sam negde gresio ispravite me. [ Nedeljko @ 10.05.2012. 19:14 ] @
Mislim da je rešenje domaćeg da se uoči da podintegralna funkcija nije definisana, pa samim tim ni zadatak.
[ patkan1992 @ 10.05.2012. 20:02 ] @
igorpet, nisam imao gresku. Samo si ti radio ovo na drugaciji nacin. :)
Nedeljko, to mi uopste nije palo na pamet. Moguce da je to, pitacu sledece nedelje na vezbama :) [ igorpet @ 10.05.2012. 20:18 ] @
Da, ispada onako kako si napisao, mada onaj - ispred integrala je greska, treba da bude +, ali posto se sve to anulira, ovog puta, nije uticalo na resenje. Mada i 0 moze biti regularno resenje :)
[ darkosos @ 10.05.2012. 20:25 ] @
[ Nedeljko @ 10.05.2012. 20:35 ] @
Ljudi, džabe računate. Podintegralna funkcija nije definisana. Treba prvo zadati granu logaritma na koju se milsi u podintegralnoj funkciji. Ovo što mućkate sa izrazima nema nikakvog smisla.
[ patkan1992 @ 10.05.2012. 20:36 ] @
darko, a sta da je to pod ln-om bilo pod apsolutnu vrednost? Kakvu razliku pravi?
EDIT: Znaci reseno je, hvala Nedeljko! :) [ igorpet @ 10.05.2012. 20:50 ] @
Grafik ove podintegralne funkcije izgleda ovako:
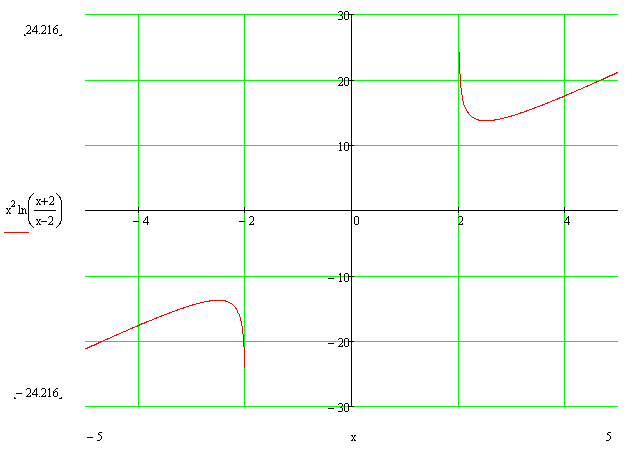 I naravno da nije definisana u ovom intervalu i da je povrsina 0. nista - nista = 0 dakle crva nije ni bilo [ darkosos @ 10.05.2012. 21:02 ] @
[ igorpet @ 10.05.2012. 21:08 ] @
Citat: darkosos: Pa, da tu stoji apsolutna zagrada, domen bi sadrzao interval integraljenja, i onda moze da se radi kako ste vec radili... S' tom razlikom da bo to prakticno bio integral 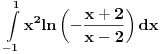 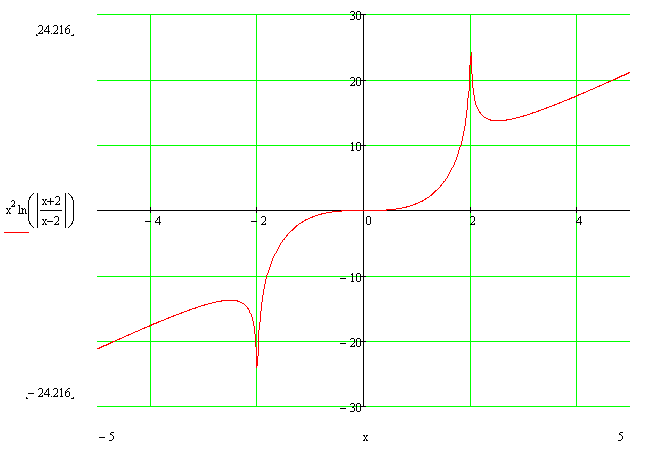 Sada bi vec nesto imalo u tom intervalu za racunanje povrsine [ patkan1992 @ 10.05.2012. 21:11 ] @
Ne komplikujte mi zivot :) Zakljucak je da ovo nije definisano :D
[ darkosos @ 10.05.2012. 21:11 ] @
Hm, pa ta funkcija izgleda poprilicno neparna, a preko intervala simetricnog u odnosu na nulu, integral ovakvih funkcija je 0.
[ cikin @ 14.10.2012. 11:09 ] @
[ ale11 @ 29.11.2012. 15:54 ] @
Da li mi možete pomoći oko rešavanja ovog integrala: ∫_0^t▒〖dt'X(t^')e^(-λ(t-t^' ) ) 〗
X nije konstantno. [ ale11 @ 29.11.2012. 15:55 ] @
Ako nije najjasnije, granice integrala su od 0 do t.
[ Sonec @ 29.11.2012. 16:03 ] @
Nista nije citljivo. Granice su najmanji problem, to se nekako i da naslutiti iz ovih hijeroglifa.
[ ale11 @ 30.11.2012. 06:46 ] @
Izvinjavam se, ali stvarno ne znam kako da postavim da se lepo vidi
Ispod integrala je dt'*X(t')*e na (-lambda*(t-t')). Unapred hvala na pomoći. [ Nedeljko @ 30.11.2012. 09:10 ] @
Mislim da neće ići kada je X proizvoljna funkcija.
[ igorpet @ 30.11.2012. 09:30 ] @
Citat: ale11: Izvinjavam se, ali stvarno ne znam kako da postavim da se lepo vidi :(. ... Odes na sledeci link: http://www.codecogs.com/latex/eqneditor.php (u pitanju je online LaTeX editor-ako si u npr. Wordu koristio opciju rada sa matematickim formulama neces imati nikakvih problema ni u ovom editoru). Otkucas postavku zadatka sa matematickim simbolima, iskopiras LaTeX kod tj. ono sto je ispisano tekstualno i ovde u tvojoj poruci to umetnes izmedju tagova [tex] i [/ tex] (stim sto izmedju ove kose crte "/" i teksta "tex" nema razmaka. Posle toga umesto "Posalji odgovor" prvo proveri kako tvoja poruka izgleda pritiskom na "Pogledaj kako odgovor izgleda". Nadam se da sam barem malo bio od pomoci. [ ale11 @ 30.11.2012. 10:00 ] @
Trebalo bi da je X neka funkcija od c/t gde je c=const
[ ale11 @ 30.11.2012. 10:02 ] @
Citat: Nedeljko: Mislim da neće ići kada je X proizvoljna funkcija. Trebalo bi da je X neka funkcija oblika C/t' gde je C=const [ ale11 @ 30.11.2012. 10:08 ] @
[quote]igorpet:
Citat: ale11: Izvinjavam se, ali stvarno ne znam kako da postavim da se lepo vidi :(. ... Odes na sledeci link: http://www.codecogs.com/latex/eqneditor.php (u pitanju je online LaTeX editor-ako si u npr. Wordu koristio opciju rada sa matematickim formulama neces imati nikakvih problema ni u ovom editoru). Otkucas postavku zadatka sa matematickim simbolima, iskopiras LaTeX kod tj. ono sto je ispisano tekstualno i ovde u tvojoj poruci to umetnes izmedju tagova  Hvala! [ Nedeljko @ 30.11.2012. 13:06 ] @
Citat: ale11: Trebalo bi da je X neka funkcija oblika C/t' gde je C=const U tom slučaju možeš da računaš samo numerički. [ Sonec @ 30.04.2013. 16:57 ] @
[ anonimnistefi @ 30.04.2013. 17:30 ] @
Nije mnogo težak ali ima da se piše. Jedna primena parcijalne integracije i jedno rastavljanje preko parcijalnih razlomaka ga manje-više rešava.
[ Sonec @ 30.04.2013. 19:15 ] @
Izvolte, demonstriraj.
[ anonimnistefi @ 30.04.2013. 19:52 ] @
[ Sonec @ 30.04.2013. 20:17 ] @
Fali ti "na kvadrat" na dva mesta. Videces i sam.
Eto, moze tako da se resi. Ja sam imao na umu resenje koje malkice koristi trigonometriju, da bi se doslo do formule 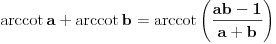 (u nasem slucaju (u nasem slucaju  i i 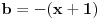 ) i posle bismo nasli ) i posle bismo nasli 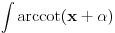 (da ne bismo racunali dva puta, za razlicite vrednosti parametra (da ne bismo racunali dva puta, za razlicite vrednosti parametra  ) na standardan nacin preko parcijalne integracije. ) na standardan nacin preko parcijalne integracije.[ anonimnistefi @ 30.04.2013. 20:34 ] @
Hm, veoma interesantno rešenje. :) Kako si to uočio?
I, ne mogu da nađem mesto gde nedostaju kvadrati... [ Sonec @ 30.04.2013. 20:56 ] @
[ andrija100 @ 06.07.2013. 13:15 ] @
E ljudi moze mala pomoc, potrebno je da izracunam povrsinu figure preko odredjenog integrala koja je ogranicena pravama y=sin(x)( 0<=x<=pi/2), y=0, y=1, i tangentom krive y=log(x) u tacki A(1,y0). Sada ja sam nasao tangentu krive y=(x-1)/ln(10) u tacki A(1,0), mislim da sam dobro postavio inetgral: (x-1)/ln(10)-sin(x). Samo me sada buni koje su granice ovog integrala, takodje sam nacrtao grafik i naso presecne tacke figure odn. njihove x koordinate a to su redom x=0, x=1, x=pi/2, x=2,457 ova poslednja je presek tangente krive y=(x-1)/ln(10) i y=sin(x), glavna pitanja da li sam dobro postavio integral i koje su granice? Hvala. :D
[ darkosos @ 06.07.2013. 16:05 ] @
Mislim da od 0 do 1 treba da se racuna samo sinus jer imas y=0 kao granicnu liniju, a od 1 do pi/2 ta razlika koju si napisao. Dalje nema nista, jer za sin imas ogranicenje do pi/2. Mada bi formalno trebalo da pise da je povrsina ogranicena i sa x=pi/2...
[ darkosos @ 06.07.2013. 16:30 ] @
A sta je problem? Primitivna funkcija se lako racuna, mozda je problem sa limesima?
[ pitomir @ 06.07.2013. 16:41 ] @
[ darkosos @ 06.07.2013. 17:04 ] @
Postupak je da nadjes prvo primitivnu funkciju, a tu te niko ne pita da li razdvajas... Prilikom zamene krajnjih tacaka, odnosno u ovom slucaju trazenja limesa, ne sme uvek da se razdvoji, ali to je vec pravlio kada je limes zbira jednak zbiru limesa.
[ pitomir @ 06.07.2013. 17:27 ] @
E, pa da, super, uspela sam da resim. Hvala puno.
[ andrija100 @ 06.07.2013. 17:56 ] @
Citat: darkosos: Mislim da od 0 do 1 treba da se racuna samo sinus jer imas y=0 kao granicnu liniju, a od 1 do pi/2 ta razlika koju si napisao. Dalje nema nista, jer za sin imas ogranicenje do pi/2. Mada bi formalno trebalo da pise da je povrsina ogranicena i sa x=pi/2... Rezulatat treba da ispadne (ln(10)-pi+4)/2. Ne dobijam to kada uradim ovako kao sto si naveo? [ darkosos @ 06.07.2013. 18:07 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|