[ anuppuke @ 25.03.2012. 19:43 ] @
| Moze li mi neko objasniti kako se trazi granicna vrijednost funkcije dvije promjenljive koristeci teoremu o ukljestenju? |
|
[ anuppuke @ 25.03.2012. 19:43 ] @
[ Sonec @ 25.03.2012. 20:02 ] @
Ogranicis funkciju sa obe strane istom vrednoscu (hm, lose sam se izrazio, shvatices vec), pa tada mora i sama funkcija da tezi toj vrednosti. Mozda ti je poznata teorema o dva policajca, e, ovo je isto to, samo za dve promenljive. Evo jedan primer (najlakse se uci preko primera):
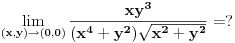 Sa jedna strane je 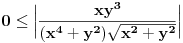 , dok sa druge vazi , dok sa druge vazi 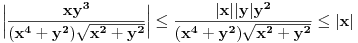 (jer je (jer je 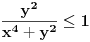 i i 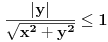 ), a to tezi 0 kada ), a to tezi 0 kada 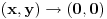 (ovde nam je, konkretno, vazno da (ovde nam je, konkretno, vazno da 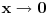 ). ).Odsnosno, imas 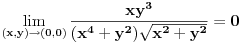 [ anuppuke @ 25.03.2012. 20:18 ] @
Hvala na odgovoru Sonec. S obzirom da nisam bas 100% ukapirao kako si rijesio taj primjer, mogu li ja da posaljem neki jednostavniji da uradis? Znam da sam dosadan ali frka mi je, kolokvijum mi se blizi :)
[ Sonec @ 25.03.2012. 20:26 ] @
Sta nisi shvatio?
Pa ti postavi, pa ako neko bude zeleo on ce pomoci. I da, reci gde je problem, dokle si stigao, ovde se ne rade zadaci ako nisi ti bar malo poceo. [ anuppuke @ 25.03.2012. 20:33 ] @
Nije mi jasno zbog cega si ogranicio nulom. Sta bi bilo da si stavio neku drugu vrijednost?
[Ovu poruku je menjao anuppuke dana 25.03.2012. u 21:45 GMT+1] [ Sonec @ 25.03.2012. 20:45 ] @
Hm, pa ovaj limes je bio jedan medju korak u dokazivanju da je odredjena funkcija diferencijabilna u tacki
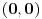 , pa je se znalo cemu bi trebalo da bude ovaj limes jednak (ako on postoji). Dobro, mozda nije najbolji primer. , pa je se znalo cemu bi trebalo da bude ovaj limes jednak (ako on postoji). Dobro, mozda nije najbolji primer.Ali, ti uvek mozes da proveris preko Hajnea cemu bi trebalo da bude jednak limes ako on postoji. Uzmes dva niza koja teze onim vrednostima kojima teze  i i  , i proveris cemu tezi cela funkcija (npr. ovde uzmes , i proveris cemu tezi cela funkcija (npr. ovde uzmes 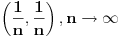 i videces da je ovaj limes (ako postoji) jednak nuli (naravno, ako nadjes dva para nizova koja teze i videces da je ovaj limes (ako postoji) jednak nuli (naravno, ako nadjes dva para nizova koja teze 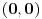 , a funkcija ne tezi istoj vrednosti, onda ne postoji dati limes). , a funkcija ne tezi istoj vrednosti, onda ne postoji dati limes).Ovo ti je u stvari prepricana Hajneova teorema. [ anuppuke @ 25.03.2012. 21:12 ] @
Evo jednog primjera sa vjezbi:
http://oi39.tinypic.com/167w01t.jpg I tu je ograniceno nulom. Gledajuci oba primjera, izgleda da je prvo potrebno pretpostaviti cemu bi limes trebao biti jednak, pa onda u zavisnosti od toga "ograniciti". [ Sonec @ 25.03.2012. 21:25 ] @
Pa nista, ovde si mogao da uzmes niz
 , kada , kada 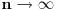 . I onda imas . I onda imas 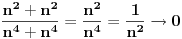 kada kada 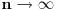 . I sad znas, ako ovaj limes postoji on ce biti nula (kao sto sam pre rekao, ako nadjes neki drugi uredjen par nizova koji zadovoljava uslove zadatka (da oba clana teze beskonacnosti), a funkcija ne tezi nuli, onda si pokazao da taj limes ne postoji). Ovo sam samo pricao kako mozes da "ulovis" cemu bi tvoja funkcja mogla teziti. . I sad znas, ako ovaj limes postoji on ce biti nula (kao sto sam pre rekao, ako nadjes neki drugi uredjen par nizova koji zadovoljava uslove zadatka (da oba clana teze beskonacnosti), a funkcija ne tezi nuli, onda si pokazao da taj limes ne postoji). Ovo sam samo pricao kako mozes da "ulovis" cemu bi tvoja funkcja mogla teziti.Ali, kada ovako ogranicavas sa obe strane, ti si time dokazao i da postoji taj limes (ne moras oko toga voditi racuna). Nadam se da sam sad bio malo jasniji. [ anuppuke @ 25.03.2012. 21:30 ] @
Sad je jasno. Hvala puno na pomoci :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|