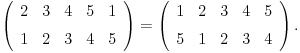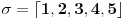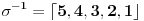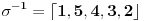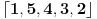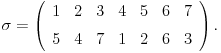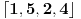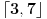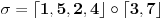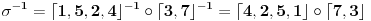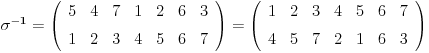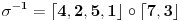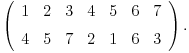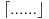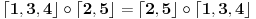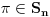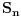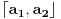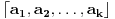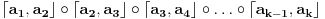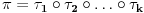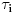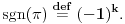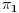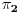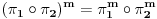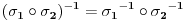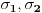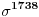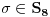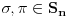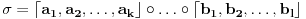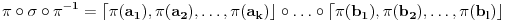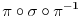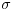http://en.wikipedia.org/wiki/Permutation#Product_and_inverse

Da napravis rucno ili masinski?

Rucno.

Recimo imam permutaciju 2, 3, 4, 5, 1
Kako se dobija inverzna permutacija?

Dakle, u pitanju je permutacija



Obrnuta je



Dakle, 5, 1, 2, 3, 4.

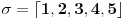
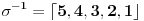
Neka je Ona se moze zapisati i kao , pa je njena inverzna permutacija koja se moze ciklicno pomeriti (siftovati) udesno dovoljan broj puta (ovde jednom) i dovesti do oblika .

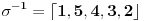
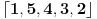
E sad, sta konkretno znaci ovakav zapis (ne znam koliko si upoznat sa njim), evo npr. ovaj poslednji , pa, 1 se slika u 5, 5 u 4, 4 u 3, 3 u 2, a 2 u 1 (dakle, ides redom), sto bas i odgovara zapisu
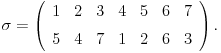
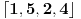
E sad, ovaj primer i nije bas najreprezentativniji da se pokaze kako se trazi inver permutacije. Evo npr. neka je Dakle, krenemo od 1 (moze i bilo koji drugi broj), i sad, 1 se slika u 5, 5 u 2, 2 u 4, 4 u 1 i zatvaramo cikl (dakle, kada se neki element cikla slika u pocetni element cikla onda zatvaramo), dakle imamo , dalje, biramo iduci broj koji se nije dosada javljao, npr. 3, i sad, 3 se slika u 7, 7 u 3 i zatvaramo cikl, tj. 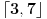, i na kraju ostaje 6, al 6 se slika u 6, pa to ne pisemo. 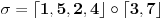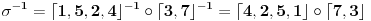I sad na kraju, nasa permutacija se moze predstaviti kao (pri cemu ovakav postupak pravi disjunktne ciklove, samim tim i oni i komutiraju (vidi pricu dole), pa vazi (mada inverz transpozicije je ista transpozicija, nema efekta). Ajd da proverimo ovo, dakle . 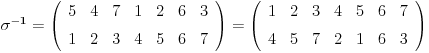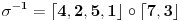I sad se vratimo na , koja kaze da se 4 slika u 2, 2 u 5, 5 u 1, 1 u 4, pa, 7 u 3, 3 u 7, i 6 u 6 (cega nema to se slika u samog sebe) sto i jeste

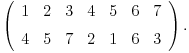
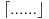
Ovakav () nacin predstavljanja permutacija je poprilicno dobar i omogucava nam da lakse operisemo sa permutacijama.

Evo nekoliko lepih osobina koje se lepo prezentuju ovakvim zapisom:

Disjunktni ciklovi komutiraju. Dakle, npr,

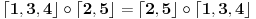
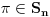
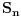
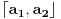
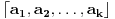
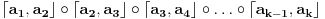
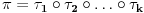
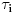
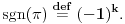
Dalje, svaka permutacija ( grupa permutacija reda ) moze se napisati kao kompozicija disjunktnih ciklova. A samim tim vazi i da se svaka permutacija moze predstaviti kao proizvod transpozicija (cikl duzine 2, npr. ), jer se svaki cikl moze prestaviti kao . E sad, ova cinjenica nam pomaze kod odredjivanja parnosti permutacije sgn, jer vazi da ako je ( su transpozicije) onda je Pri cemu bi trebalo obratiti na to da predstavljanje permutacije na proizvod transpozicija nije jedinstveno, ail parnost ce uvek biti ista.

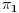
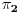
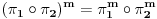
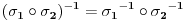
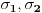
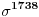
Ako permutacije i komutiraju, onda je . E, ova osobina nam pomaze kod trazenja inverza jer vazi (gde su disjuktne, a samim tim i komutiraju). Poprilicno korisna stvar ako se jos zna i pojam reda elementa u grupi, za odredjivanje npr. gde je .

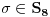
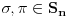
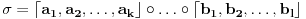
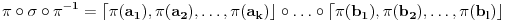
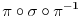
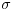
E ova je bas dobra, neka su i proizvod disjunktnih ciklova. Tada vazi ( u stvari predstavlja konjugovanje elementa elementom ).