[ Nepoznat covek @ 02.04.2012. 19:51 ] @
| Napisati jednačinu kružnice koja sadrži tačke M(10,9) N(4,3), a centar joj je na pravoj: 2x-3y+19=0. Pomoć. Radim već pola sata zadatak drugu, ali davno beše, pozaboravljao sam.. |
|
[ Nepoznat covek @ 02.04.2012. 19:51 ] @
[ darkosos @ 02.04.2012. 20:06 ] @
[ Nepoznat covek @ 02.04.2012. 20:15 ] @
e, to me je bunilo... kako da se odredi da li data tačka zadovoljava uslov?
[ darkosos @ 02.04.2012. 20:19 ] @
Mislis da pripada pravoj? Pa bre 2p-3q+19=0.
[ Nepoznat covek @ 02.04.2012. 20:23 ] @
Uh bre..
Hvala ti [ Sprečo @ 09.04.2012. 08:43 ] @
Još teže bi ti bilo da si učio po ovom udžbeniku:
Vojislav Mihailović, napisao je 1964.g. udžbenik – Geometrija – za drugi razred gimnazije prirodno-matematičkog smjera (recenzenti: Zdravko Mihailović i Olga Mitrinović). U navedenom udžbeniku, na strani 39. piše: Definicija 10. Skup svih tačaka u jednoj ravni podjednako udaljenih od jedne tačke te ravni naziva se krug. Da se ne radi o „štamparskoj grešci“ napomenut ću da u cijelom udžbeniku (148 stranica) kružnica nije pomenuta ni jedan jedini put. Za navedene matematičare – kao da taj pojam i ne postoji!? [ Sonec @ 09.04.2012. 11:33 ] @
Nedeljko ti je vec odgovorio. Evo, da budemo precizniji:
Citat: Neka je 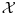 pramen pravih i pramen pravih i  proizvoljna tacka u ravni proizvoljna tacka u ravni  tog pramena koja ne pripada svim pravama pramena tog pramena koja ne pripada svim pravama pramena 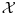 . Skup svih tacaka ravni . Skup svih tacaka ravni  , osnosimetricnih tacki , osnosimetricnih tacki  u odnosu na prave pramena u odnosu na prave pramena 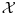 cemo zvati epicikom i obelezavacemo ga sa cemo zvati epicikom i obelezavacemo ga sa  . .Ako je 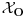 pramen konkurentnih pravih, epicikl pramen konkurentnih pravih, epicikl 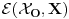 cemo zvati krugom. Tacku cemo zvati krugom. Tacku  cemo zvati sredistem ili centrom toga kruga, a duz cemo zvati sredistem ili centrom toga kruga, a duz 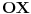 njegovim poluprecnikom ili radijusom. Krug cemo obelezavati i sa njegovim poluprecnikom ili radijusom. Krug cemo obelezavati i sa  U toj oznaci U toj oznaci  je srediste, a je srediste, a  poluprecnik kruga poluprecnik kruga  . Neposredno se dokazuje da krug . Neposredno se dokazuje da krug 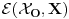 istovetan sa skupom svih tacaka istovetan sa skupom svih tacaka  ravni kojoj pripada, takvih da je ravni kojoj pripada, takvih da je 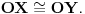 (str. 135) (str. 135) ................................................................................ ................................................................................ Unijom kruga i njegove unutrasnjosti cemo zvati i kruznom povrsi, a sam krug cemo ponekad zvati i rubom te povrsi. (str. 138) Zoran Lucic, Euklidska i hiperbolicka GEOMETRIJA Takodje, na 312 strana se nigde ne pominje termin kruznica. Ne vidim neki problem zbog toga. [ Nedeljko @ 09.04.2012. 15:58 ] @
Sprečo, problem sa tom definicijom kruga je što to konstantno rastojanje može biti i nula, tj. nije isključeno definicijom, a jedna tačka se ipak ne smatra krugom.
Kod Lučića se ono što se inače zove krug zove kružna površ, a ono što se inače zove kružnica se zove krug. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|