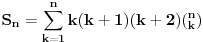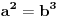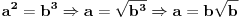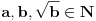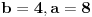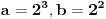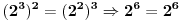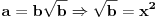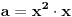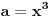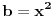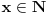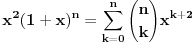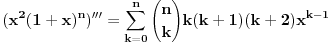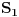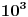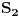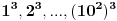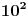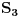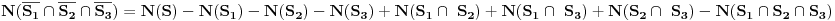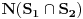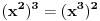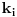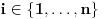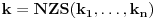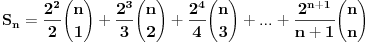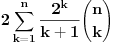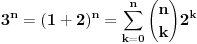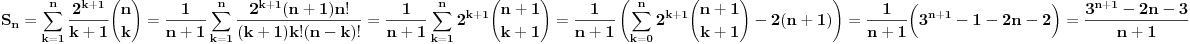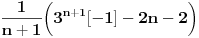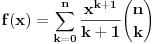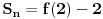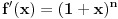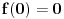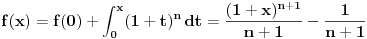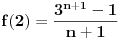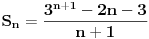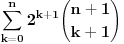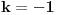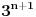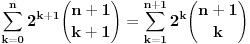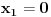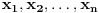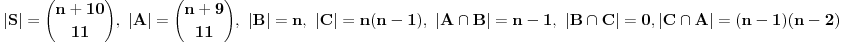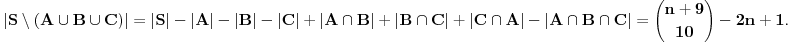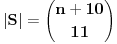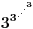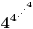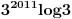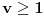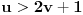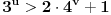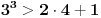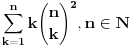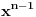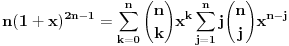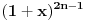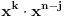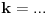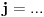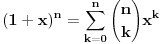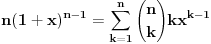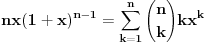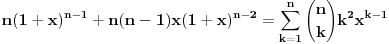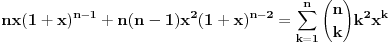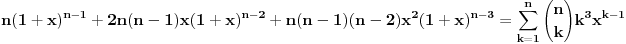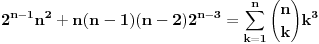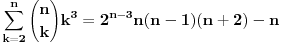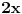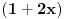[ elementarna.nepogoda @ 16.04.2012. 12:08 ] @
|
[ lonelyrider_44 @ 16.04.2012. 13:12 ] @
[ elementarna.nepogoda @ 16.04.2012. 15:50 ] @
Hvala puno, razumeo .
Sad si me ovim odgovorom bacio na muke dodatno. Naime, moj zadatak je bio da ustanovim koliko ima brojeva od 1 do 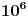 koji nisu ni potpuni kvadrati, ni kubovi, ni četvrti stepeni nekog prirodnog broja. Ideja mi je bila da prebrojim one koji jesu bar nešto od toga, pa da oduzmem. E sad, čini mi se da je skup "četvrtih stepena" podskup "potpunih kvadrata", a u početku sam mislio da su potpuni kvadrati disjunktni (osim jedinice) sa kubovima. Sad si me demantovao, pa pomozi da razgraničim i to koji nisu ni potpuni kvadrati, ni kubovi, ni četvrti stepeni nekog prirodnog broja. Ideja mi je bila da prebrojim one koji jesu bar nešto od toga, pa da oduzmem. E sad, čini mi se da je skup "četvrtih stepena" podskup "potpunih kvadrata", a u početku sam mislio da su potpuni kvadrati disjunktni (osim jedinice) sa kubovima. Sad si me demantovao, pa pomozi da razgraničim i to Dakle, treba mi broj elemenata unije ova tri skupa ali mi problem prave preseci. [ Harx @ 16.04.2012. 18:22 ] @
Ne znam da li je moguće tako rešiti kako ti želiš , mi smo imali skoro isti ovakav zadatak iz kombinatorike i treba da se koristi "Formula uključenja-isključenja". Dakle, ako ste učili tu formulu, onda koristi to...
[ elementarna.nepogoda @ 16.04.2012. 19:31 ] @
Ako ti nije problem, napiši reč-dve o rešenju.
Po formuli uključenja-isključenja, trebaće mi kardinalnosti preseka, a do tih brojeva ne umem da dođem [ Nedeljko @ 16.04.2012. 20:32 ] @
[ Harx @ 16.04.2012. 20:39 ] @
[ Nedeljko @ 16.04.2012. 23:33 ] @
[ lonelyrider_44 @ 17.04.2012. 14:32 ] @
Citat: elementarna.nepogoda: Nedeljko, hoćeš da kažeš da se u preseku kvadrata i kubova zapravo nalaze šesti stepeni ? :) Citat: [ elementarna.nepogoda @ 17.04.2012. 14:32 ] @
hvala na pomoći, u pravu si
[ elementarna.nepogoda @ 20.04.2012. 23:19 ] @
[ darence @ 21.04.2012. 07:35 ] @
[ Sonec @ 21.04.2012. 09:22 ] @
[ elementarna.nepogoda @ 02.05.2012. 23:53 ] @
imam novi problem.
Koliko ima n-tocifrenih brojeva sa zbirom cifara 11 ? Jedino sto znam je da se 11 moze zapisati sa najmanje dve a najvise 11 cifara ali problem su i nule kojih moze biti koliko hoces... Takodje mogu biti i na pocetku broja, sto unosi dodatnu zabunu. Molio bih za pomoć [ darkosos @ 03.05.2012. 08:06 ] @
Kako na pocetku broja? 003 je trocifren broj? Pa onda je i stocifren :) Ako se trazi tako nesto onda je pogresno reci n-tocifren broj, mozda uredjena n-torka cifara ili slicno...
[ Sonec @ 03.05.2012. 10:42 ] @
[ elementarna.nepogoda @ 03.05.2012. 12:53 ] @
Citat: Kako na pocetku broja? 003 je trocifren broj? Pa onda je i stocifren :) Ako se trazi tako nesto onda je pogresno reci n-tocifren broj, mozda uredjena n-torka cifara ili slicno... ma imao sam neku ideju preko kombinacija ali bi ona ukljucivala i nule na pocetku broja, sto je problematicno... [ elementarna.nepogoda @ 03.05.2012. 13:07 ] @
Citat: hvala. Da li neko može da objasni ovo malo detaljnije? [ Sonec @ 03.05.2012. 21:11 ] @
Postoji teorema koja kaze da broj nenegativnih resenja jednacine
 (gde su (gde su 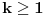 i i 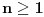 ) iznosi ) iznosi 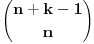 . Dokaz ovog tvrdjenja mozete naci OVDE, strana 111. (ne mora bas preko ove teoreme, moze i preko posmatranja varijacija odredjenog tipa) . Dokaz ovog tvrdjenja mozete naci OVDE, strana 111. (ne mora bas preko ove teoreme, moze i preko posmatranja varijacija odredjenog tipa)I mislim da je sad jasno zasto je 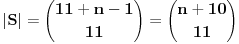 . .Dalje, mislim da je jasno zasto posmatramo jednacinu  . E sad, koja nama ovde resenja ne valjaju? Pa, ako je prva cifra nula, onda nam to resenje ne valja, jer onda to nije n-tocifreni broj, vec n-1-tocifren (il cak i manje, ako imas jos takvih nula). Da bi nasli koliko je takvih resenja, msm da je jasno da se to svodi na odredjivanje koliko jednacina . E sad, koja nama ovde resenja ne valjaju? Pa, ako je prva cifra nula, onda nam to resenje ne valja, jer onda to nije n-tocifreni broj, vec n-1-tocifren (il cak i manje, ako imas jos takvih nula). Da bi nasli koliko je takvih resenja, msm da je jasno da se to svodi na odredjivanje koliko jednacina  ima resenja. Takodje, nama su ima resenja. Takodje, nama su  jednocifreni brojevi, tako da nam ne odgovaraju ni resenja u kojima je za neko jednocifreni brojevi, tako da nam ne odgovaraju ni resenja u kojima je za neko 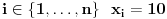 , odnosno , odnosno 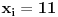 . Dakle, od svih resenja, oduzecemo uniju ovakvih resenja (koja nam ne valjaju), i primeniti princip ukljucenja-iskljucenja. Ako je . Dakle, od svih resenja, oduzecemo uniju ovakvih resenja (koja nam ne valjaju), i primeniti princip ukljucenja-iskljucenja. Ako je 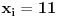 , onda su ostali clanovi jednaki nuli (dakle, jedinstveno su odredjeni), tako da nam ostaje samo da kazemo da imamo , onda su ostali clanovi jednaki nuli (dakle, jedinstveno su odredjeni), tako da nam ostaje samo da kazemo da imamo  nacina kako cemo da dodelimo vrednost 11 nekom nacina kako cemo da dodelimo vrednost 11 nekom  . Slicno za slucaj ako je . Slicno za slucaj ako je 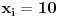 (za neko (za neko  ), onda je jos jedan broj jednak jedinici, a ostali su nuli. Dakle, imamo n mogucnosti za to kome cemo da dodelimo 10 (ili 1, svejedno je), a zatim za n-1 broj odredjujemo kome cemo da dodelimo 1, dakle, ukupno ), onda je jos jedan broj jednak jedinici, a ostali su nuli. Dakle, imamo n mogucnosti za to kome cemo da dodelimo 10 (ili 1, svejedno je), a zatim za n-1 broj odredjujemo kome cemo da dodelimo 1, dakle, ukupno 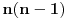 . Za formulu ukljucenja-iskljucenja nam trebaju i neki preseci, al to mozes i sam da vidis zbog cega je njihova kardinalost tolika (koliko je napisano). . Za formulu ukljucenja-iskljucenja nam trebaju i neki preseci, al to mozes i sam da vidis zbog cega je njihova kardinalost tolika (koliko je napisano).[ darkosos @ 03.05.2012. 22:07 ] @
Ha, sjajno, pogledao sam taj dokaz, odusevila me jednostavnost. Jos jedan dokaz da je ideja, tj. pristup, veoma vazan u matematici. Ja sam se neko vreme cesao po glavi, pokusavajuci da dobijem tu opstu formulu, dobro je da sam odustao :) U svakom slucaju, mislim da je ovo vazan deo zadatka (mozda jedini netrivijalan). Posto je tekst na engleskom, a i malo je sazet, ja cu prepricati (ako dozvoljavate :) taj dokaz ovde:
Neka su dati n i k; treba  pretvoriti u nesto kombinatorno iskazivo: pretvoriti u nesto kombinatorno iskazivo:zamislimo n + k - 1 "kucica" i da treba da izaberemo k-1 od njih u koje postavimo znak "+", sto ostavlja n praznih kucica; korespodencija sa datom jednacinom je sledeca: ako niz uzastopnih kucica zamenimo sa njihovim brojem (dakle 2 prazne uzastopne kucice su 2 itd), dobijamo jednu mogucu varijantu trazenog zbira; pritom, ako nema kucica izmedju dva znaka +, to zamenjujemo sa 0 (ako niz pocinje sa + ili zavrsava sa +, to je takodje 0); s' obzirom da praznih kucica ima n, ukupan zbir ovih brojeva jeste n. Radi ilustracije, evo jednog primera za n=4, k=5: . . + + . + . + korespondira 2 + 0 + 1 + 1 + 0. Ovakvih izbora ima, naravno, 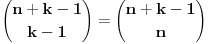 [ elementarna.nepogoda @ 04.05.2012. 16:01 ] @
puno hvala na objašnjejima. Nisam ni slutio da je rešenje do te mere komplikovano.
[ darkosos @ 04.05.2012. 19:55 ] @
Pa, sad, pitanje je sta vam je dato na raspolaganje. Npr, da li u arsenalu imate tu teoremu koju je Sonec naveo, u vezi resenja jednacine sa k nepoznatih u N0... Mislim da svakako nije namera zadatka da se ona dokazuje. Navedeno resenje direktno se oslanja na tu teoremu, prilagodjavajuci rezultat zadatku; dakle ocigledno nije jednostavno primeniti direktnu logiku, tj. naci ta resenja u skupu cifara. Dalje, izgleda kao i da broj 11 nije slucajno izabran, jer je dovoljno izbaciti samo 10 i 11; zamisli da je tu neki pristojno veci broj, ko bi napravio sve te preseke i odredio im broj elemenata...
Dakle, ja bih zakljucio da je namera zaista koriscenje pomenute teoreme (osim ako postoji neki laksi direktan nacin, sto izgleda malo verovatno). Ostalo je manje-vise prosta logika, racunajuci i kombinatorni deo i deo oko formule za broj elemenata skupa S\{AuBuC}. [ elementarna.nepogoda @ 21.05.2012. 00:32 ] @
[ Nedeljko @ 21.05.2012. 02:32 ] @
[ elementarna.nepogoda @ 17.06.2012. 21:27 ] @
[ Sonec @ 17.06.2012. 22:36 ] @
[ elementarna.nepogoda @ 17.06.2012. 23:29 ] @
Pavle Mladenović verovatno ume da dođe do tog rešenja. Ja -ne
[ Sonec @ 18.06.2012. 00:09 ] @
[ nePonovljivA @ 17.11.2012. 15:01 ] @
Da ne otvaram novu temu, pitaću ovde.
Kaže, izračunati sumu 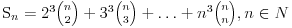 Čini mi se da je ova suma jednaka 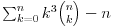 jer moramo odbiti prve članove ali dalje ne umem. Ovaj pokušaj je bio usmeren na neko eventualno iskorišćavanje binomnog obrasca, ali... :( Ne umem da fiksiram ovaj eksponent, a da mi suma vrti osnovu. Kod binomnog je obratno jer moramo odbiti prve članove ali dalje ne umem. Ovaj pokušaj je bio usmeren na neko eventualno iskorišćavanje binomnog obrasca, ali... :( Ne umem da fiksiram ovaj eksponent, a da mi suma vrti osnovu. Kod binomnog je obratnoTakođe, zadatak kaže za 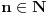 ali meni nije jasno npr za ali meni nije jasno npr za  . Ispada da se javlja . Ispada da se javlja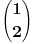 . .Ako može pomoć ;) [ Sonec @ 17.11.2012. 18:18 ] @
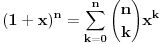 , uzmimo , uzmimo 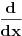 na obe strane, dobijamo na obe strane, dobijamo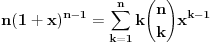 , pomnozimo sa , pomnozimo sa  , dobijamo , dobijamo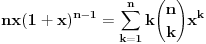 , uzmimo , uzmimo 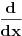 na obe strane, dobijamo na obe strane, dobijamo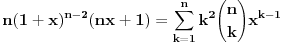 , pomnozimo sa , pomnozimo sa  , dobijamo , dobijamo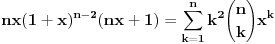 , uzmimo , uzmimo 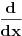 na obe strane, dobijamo na obe strane, dobijamo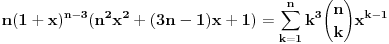 , pomnozimo sa , pomnozimo sa  , dobijamo , dobijamo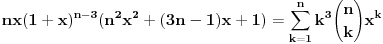 Stavimo da je  , dobijamo , dobijamo 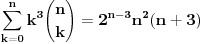 Prema tome, konacno resenje je 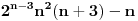 Za tvoje pitanje: http://mathworld.wolfram.com/BinomialCoefficient.html [ Nedeljko @ 17.11.2012. 18:26 ] @
[ nePonovljivA @ 17.11.2012. 20:26 ] @
Zahvaljujem na detaljnom rešenju.
Da li možda znate u kojoj zbirci može da se nađe ovaj zadatak i još neki njemu slični ? [ Nedeljko @ 18.11.2012. 06:35 ] @
Meni su se potkrale neke greške u računu, ali postupak je taj. Sonec je izračunao tačno.
[ zzzz @ 18.11.2012. 11:13 ] @
[ Sonec @ 02.12.2012. 22:16 ] @
Citat: nePonovljivA: Zahvaljujem na detaljnom rešenju. Da li možda znate u kojoj zbirci može da se nađe ovaj zadatak i još neki njemu slični ? Mozes besplatno skinuti sledece dve knjige (dobro, to nisu knjige, vec linkovi ka tim knjigama (nisam hteo da postavljam direktne linkove do pdf-a)): http://www.math.upenn.edu/~wilf/AeqB.html http://www.math.upenn.edu/~wilf/DownldGF.html [ Sonec @ 26.03.2013. 20:05 ] @
Citat: Inace, za ovaj zadatak ima mnogo lepse (bar za mene) resenje. Naime, neka je 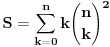 (primetimo da ovde sumacija pocinje od nule, al to nece uticati na krajnji rezultat). Primetimo da tada (poznajuci osobine o binomnim koeficijentima i uvodjenjem linearne smene) (primetimo da ovde sumacija pocinje od nule, al to nece uticati na krajnji rezultat). Primetimo da tada (poznajuci osobine o binomnim koeficijentima i uvodjenjem linearne smene) 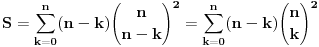 . Sabirajuci ovakva dva predstavljanja zadate sume nalazimo . Sabirajuci ovakva dva predstavljanja zadate sume nalazimo 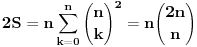 , odnosno , odnosno 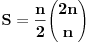 (sto se poklapa sa prethodnim resenjem (sto se poklapa sa prethodnim resenjem 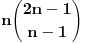 , ko ne veruje neka izracuna). Jednakost , ko ne veruje neka izracuna). Jednakost 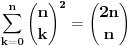 nalazi se gledanjem koeficijenta uz nalazi se gledanjem koeficijenta uz 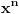 u u 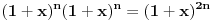 . .Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|