[ maridza988 @ 18.04.2012. 20:31 ] @
|
| Jel ima neko ideju kako rešiti sledeći zadatak... Ja sam pokušavala i ništa!
Odrediti višestrukost nule a polinoma:
q(x)={(x-a)/2} * [p`(x) + p`(a)] - p(x) + p(a).
Hvala vam unapred na pomoći! |
[ Sonec @ 18.04.2012. 20:42 ] @
Ako je
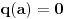
onda je

nula polinoma
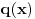
.
Zatim, proveris da li je

nula polinoma
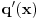
(trazis prvi izvod, po

), i ako je

nula tog polinoma, onda je

dvostruka nula.
Dalje proveravas za
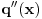
, dokle god moze. Prvi put kad naidjes da nije, onda stajes.
[ darkosos @ 18.04.2012. 20:49 ] @
To bi trebalo da bude najveci izvod polinoma koji a anulira + 1. Npr ako je q(k)(a)=0 a q(k+1)(a)<>0 onda je nula reda k+1.
[ maridza988 @ 18.04.2012. 21:06 ] @
Ok, znam ja to sve, mene bune ovi p(x) i p(a) i njihovi izvodi!
[ darkosos @ 18.04.2012. 21:22 ] @
q'(x) = 1/2(p'(x)+p'(a)) + (x-a)/2 p'(x) - p'(x) pa je q'(a) = 0... Ne znam za dalje ali ovde nije potrebno znati nista o p.
[ maridza988 @ 18.04.2012. 21:35 ] @
Hvala za prvi izvod,ali za drugi ne znam kako dalje jer se dobija:
q"(x)= 1/2 p"(x) + 1/2 P(3)(x) - p"(x)
q"(x)= 1/2(p(3)(x) - p"(x))
[ darkosos @ 18.04.2012. 21:47 ] @
Izgleda da sam pogresno napisao prvi izvod, trebalo bi q'(x) = 1/2(p'(x)+p'(a)) + (x-a)/2 p''(x) - p'(x) pa bi bilo q''(x) = (x-a)/2 p'''(x) pa je opet q''(a) = 0.
Sori, stopili su mi se apostrofi zbog dioptrije :)
[ maridza988 @ 18.04.2012. 23:00 ] @
Izvini, hvala ti puno na pomoci. Moracu da obnovim izvode!!! Davno to nisam radila

[ Nedeljko @ 18.04.2012. 23:11 ] @
Ja bih to radio preko Tejlorovog razvoja polinoma
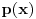
u okolini tačke

. Dakle,
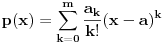
,
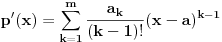
,
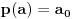
,
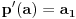
,
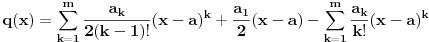
Posle kraćeg računa je
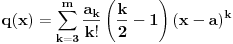
.
Dakle, ako je polinom
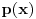
stepena dva ili manjeg, onda je
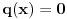
. U suprotnom je

nula reda

polinoma
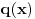
, gde je

najmanji prirodan broj koji nije manji od 3 i takav da je
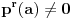
, odnosno red broja

kao nule polinoma
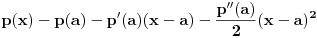
.
Posebno, važi
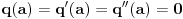
.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.