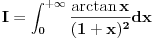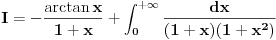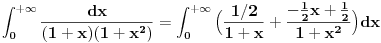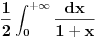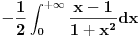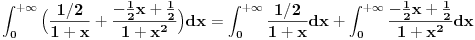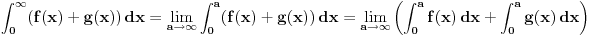Ne. Ako integral od f divergira i integral od g divergira, to i dalje ne znači da integral od f+g divergira.

Prvo integrali sve od 0 do a, pa kad sve to izračunaš, onda pusti da a teži beskonačnosti.

Kao neodređen integral rešenje je:

I= 1/2*ln(1+x) - 1/4*ln(1+x^2) + 1/2*arctg(x) od nula do g, a posle pustiš limes da g teži u beskonačnost.

Prva dva ln-a spojiš u jedan i dobićeš da konvergira ka pi/4.

Znači, ja smem da rešim integral kao neodređeni, pa tek na kraju da vratim granice, tj. pustim limes? Jer evo u ovom koraku ja mislim da ne sme ovako da se piše:

,

jer ova dva integrala sa desne strane divergiraju.

Ajd da pričamo o 3 integrala, jer taj drugi razbijaš na dva: ln i arctg.
Mislim da znaš da arctg(X) teži ka pi/2, kada X teži u plus beskonačnost.
Prvi integral je u rešenju je ln i on divergira ka +beskonačno.
Drugi je takođe ln i on divergira ka -beskonačno.
beskonačno minus beskonačno je neodređeni oblik limesa i ne mora biti beskonačno, može biti i konačno.
Udružiš ta 2 ln-a i dobiješ rezultat.

Kao što si i rekla:
- uradiš neodređeni integral,
- zameniš donju granicu da je nula a gronju recimo G.
- onda limes da G teži u plus beskonačno.

i dobiješ rezultat pi/4.

Ja bih ga ispisao kao u slici u prilogu.
Nisam ni koristio G.

_{[Ovu poruku je menjao miki069 dana 19.04.2012. u 22:36 GMT+1]}

.

U opštem slučaju, poslednji limes ne možeš razbiti na dva (osim ako je jedan konvergentan). Je li sada jasnije?

Ahaa, ok, sad shvatam. To me je bas bunilo. Hvala vam puno obojici!