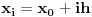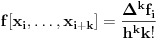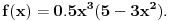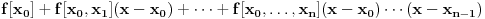|
|
[ ___ @ 21.04.2012. 23:02 ] @
|
| Da ne dužim, da li mi neko može razjasniti sledeće:
1. Imam neki polinom, recimo stepena 5...i traži se da se interpolira polinomom stepena 6. Zašto je to u stvari jedan te isti polinom? Kako je to uopšte smislen zahtev?
2. Zašto za konačne razlike, čvorovi interpolacije moraju biti ekvidistantni?
Hvala unapred. |
[ Sonec @ 21.04.2012. 23:27 ] @
Sto se tice drugog pitanja, mislim da je vazno da cvorovi budu ekvidistantni da bismo mogli iz veze izmedju konacnih i podeljenih razlika (ako je 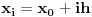 (dakle, cvorovi su ekvidistantni), onda je 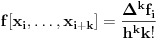 ) izvedemo Njutnov interpolacioni polinom za interpolaciju unapred, iz njega Njutnov za interpolaciju unazad, pa zatim Gausov za unapred i unazad, Stirlingov i Beselov (sve su to interpolacioni polinomi sa ravnomerno rasporedjenim cvorovima). Verujem i da samo ime, konacne razlike, nam govori da je tablica ekvidistantna. Ne znam koliko ima smisla posmatrati "konacne" razlike (po definiciji) ako tablica nije ekvidistantna (da li nam to necemu sluzi).
Prvo pitanje mi nije bas najjasnije, mozda da das neki konkretan primer/zadatak. Nije mi jasno zasto bismo polinom interpolirali, kad su nam polinomi zgodni za rad. [ Nedeljko @ 22.04.2012. 00:28 ] @
1. Neka je p(x) polinom stepena 5. Postoji tačno jedan polinom q(x) stepena najviše 6 koji prolazi proz datih 7 čvorova. Ako su ti čvorovi izabrani tako da p(x) prolazi kroz njih, onda p(x) zadovoljava te uslove, pa je on taj polinom.
2. Kod konačnih razlika čvorovi ne moraju biti ekvidistantni.
[ ___ @ 22.04.2012. 08:26 ] @
Citat: Nedeljko: 1. Neka je p(x) polinom stepena 5. Postoji tačno jedan polinom q(x) stepena najviše 6 koji prolazi proz datih 7 čvorova. Ako su ti čvorovi izabrani tako da p(x) prolazi kroz njih, onda p(x) zadovoljava te uslove, pa je on taj polinom.
Je l bi to bila teorema koja nam govori o egzistenciji i jedinstvenosti interpolacionog polinoma stepena n kroz n+1 čvor? Pošto u formulaciji ne vidim reč "najviše", a baš to i jeste ono što me buni...
Citat: Nedeljko:
2. Kod konačnih razlika čvorovi ne moraju biti ekvidistantni.
Kako to?
Citat: Sonec:
Prvo pitanje mi nije bas najjasnije, mozda da das neki konkretan primer/zadatak. Nije mi jasno zasto bismo polinom interpolirali, kad su nam polinomi zgodni za rad.
Zadatak je sa testa iz predmeta Uvod u numeričku matematiku. Ujedno tako i glasi, data je funkcija 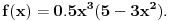
Napisati interpolacioni polinom 6. stepena na ravnomernoj mreži na segmentu [0, 1].
Kažu da je trik - zadatak... [ darkosos @ 22.04.2012. 09:21 ] @
Pa s' obizrom na tu teoremu, ako uzmes 6 ili vise tacaka, dobices bas f(x), tj polinom stepena 5.
Evo jednog polinoma stepena 6, koji bi prosao kroz 6 tacaka a ima iste vrednosti kao f(x) u tim tackama:
(x-x1)(x-x2)(x-x3)(x-x4)(x-x5)(x-x6) + f(x).
Da li to moze biti resenje zadatka?
[ ___ @ 22.04.2012. 09:47 ] @
Kažu da je rešenje baš dati polinom, koji se interpolira.
Da vas pitam: Kroz n + 1 tačku postoji jedinstven polinom stepena n koji prolazi kroz njih, ali postoji još beskonačno polinoma višeg stepena koji sadrže te iste tačke, zar ne?
Mislim da sam shvatila ovo, reč najviše objašnjava stvar, kroz 7 čvorova može se provući polinom najviše stepena 6, ali kroz te tačke već prolazi polinom stepena 5, pa je tu poslu i kraj...(mogu se nalaziti svih sedam na nekoj pravoj, pa se može aproksimirati i polinomom prvog stepena...)
Hvala vam puno ljudi!
[ ___ @ 22.04.2012. 09:49 ] @
Citat: darkosos: Pa s' obizrom na tu teoremu, ako uzmes 6 ili vise tacaka, dobices bas f(x), tj polinom stepena 5.
Evo jednog polinoma stepena 6, koji bi prosao kroz 6 tacaka a ima iste vrednosti kao f(x) u tim tackama:
(x-x1)(x-x2)(x-x3)(x-x4)(x-x5)(x-x6) + f(x).
Da li to moze biti resenje zadatka?
Verovatno je i to jedno od mogućih rešenja...mislim, zadovoljava uslove interpolacije koliko ja vidim  Hvala na ideji, poslužiće! [ Nedeljko @ 22.04.2012. 15:27 ] @
Tačan iskaz teoreme je "stepena najviše n", a ostalo je greška.
Ako mi ne veruješ, probaj da nađeš kvadratnu funkciju koja prolazi kroz tri kolinearna čvora.
U dokazu se dokazuje da postoji tačno jedno rešenje po neodređenim koeficijentima i nigde se ne dokazuje da je koeficijent uz xn različit od nule. Koeficijenti mogu biti bilo kakvi.
Stoga se interpoliranjem polinoma petog stepena polinomom šestog stepena dobija interpolirani polinom petog stepena.
A što se konačnih razlika tiče, ne znam šta drugo da ti kažem, sem da pogledaš teoriju. Čvorovi ne moraju biti ekvidistantni.
[ ___ @ 22.04.2012. 16:11 ] @
Citat: Nedeljko: Tačan iskaz teoreme je "stepena najviše n", a ostalo je greška.
Ako mi ne veruješ, probaj da nađeš kvadratnu funkciju koja prolazi kroz tri kolinearna čvora.
U dokazu se dokazuje da postoji tačno jedno rešenje po neodređenim koeficijentima i nigde se ne dokazuje da je koeficijent uz x n različit od nule. Koeficijenti mogu biti bilo kakvi.
Stoga se interpoliranjem polinoma petog stepena polinomom šestog stepena dobija interpolirani polinom petog stepena.
A što se konačnih razlika tiče, ne znam šta drugo da ti kažem, sem da pogledaš teoriju. Čvorovi ne moraju biti ekvidistantni.
- Nemam šta da verujem ili ne verujem, gore sam to konstatovala. Kao što rekoh, upravo to mi je i razjasnilo stvar, zahvaljujem.
U stvari, teorema koju ja gledam kaže da se kroz n + 1 čvor može provući jedinstven polinom stepena n, i ništa više o drugim polinomima koji sadrže iste tačke [što ne znači da ne može i višeg i nižeg, samo je ovaj jedinstven...} Ne znam na šta mislite kad kažete da je greška?
- Upravo gledam udžbenik, piše: Kad su čvorovi ravnomerno raspoređeni sa korakom h, umesto podeljenih koriste se konačne razlike. Pa umem da čitam ako ništa drugo :)
Možda ste Vi slušali neki napredniji kurs, ja sam sada na uvodnom tek, tako da se definišu na neekvidistantnoj tablici... [ Nedeljko @ 22.04.2012. 21:25 ] @
Dakle, kad su čvorovi ekvidistantni, koriste se konačne razlike. Gde pročita da su podeljene neprimenljive na slučaj čvorova koji nisu ekvidistantni?
Što se polinoma tiče, kroz pet vorova prolazi beskonačno mnogo polinoma stepena deset (ne mora baš deset, može bilo koji broj koji nije manji od pet), ali tačno jedan stepena nižeg od pet.
[ markob15 @ 23.04.2012. 01:07 ] @
@Nedeljko
Citat: Gde pročita da su podeljene neprimenljive na slučaj čvorova koji nisu ekvidistantni?
Hteo si reci konacne razlike. Buduci da o tome pricate.
Citat: 2. Kod konačnih razlika čvorovi ne moraju biti ekvidistantni. [ ___ @ 23.04.2012. 09:32 ] @
Ok, zaključak: nekad u životu videću primenu konačnih razlika i na neekvidisantnim čvorovima...do tad, kad jesu ekvidistantni, meni je to znak da razmišljam o konačnim razlikama. Valjda je to sad to :)
Mada, baš kad smo ovako načeli priču, možda je neko mogao da pročita između redova i da shvati moje pitanje i onako formulisano..otprilike, "Zašto je to baš tako?". No nema ni veze...
Hvala puno svima na uloženom trudu i pomoći.
[ Sonec @ 23.04.2012. 09:46 ] @
Citat: ___: Mada, baš kad smo ovako načeli priču, možda je neko mogao da pročita između redova i da shvati moje pitanje i onako formulisano..otprilike, "Zašto je to baš tako?".
Pa, ja sam dao jedan od mogucih odgovora:
Citat: Sonec: mislim da je vazno da cvorovi budu ekvidistantni da bismo mogli iz veze izmedju konacnih i podeljenih razlika (ako je 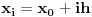 ( dakle, cvorovi su ekvidistantni), onda je 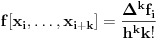 ) izvedemo Njutnov interpolacioni polinom za interpolaciju unapred, iz njega Njutnov za interpolaciju unazad, pa zatim Gausov za unapred i unazad, Stirlingov i Beselov (sve su to interpolacioni polinomi sa ravnomerno rasporedjenim cvorovima) [ Nedeljko @ 23.04.2012. 10:21 ] @
Podeljene razlike su primenljive na opšti slučaj, a konačne razlike su specijalan slučaj podeljenih razlika za ekvidistantne čvorove.
Postoji teorema koja kaže da se za proizvoljne čvorove  interpolacioni polinom funkcije  može zapisati kao
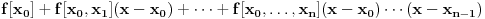 . [ Sonec @ 23.04.2012. 10:34 ] @
To je Njutnov interpolacioni polinom sa podeljenim razlikama.
Eto, i sam si na kraju rekao da su konacne za ekvidistantne cvorove.
[ Nedeljko @ 23.04.2012. 13:13 ] @
Celo vreme sam bio u zbunu. Da, mislio sam da pita zašto se podeljene razlike koriste samo za ekvidistantne čvorove i još ponovio "konačne". No, dobro.
Što se polinoma koji sam napisao tiče, on može biti i Njutnov unapred i Njutnov unazad i Gausov unapred i Gausov unazad, sve u zavisnosti od redosleda kojim biraš čvorove. Nigde nisam napisao da je niz  rastući. [ Sonec @ 23.04.2012. 13:20 ] @
Da, moze biti, al samo ako su cvorovi ekvidistantni. Inace ne.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|