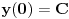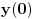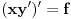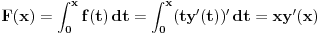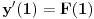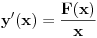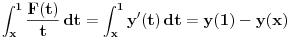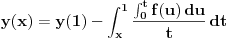Pa sad, sto se tice Greena, ne znam, ali ovo sto pitas zvuci kao da je pisac hteo da kaze da je funkcija ogranicena u 0, mada sam taj zapis nije najsrecniji...

I dalje ne znam kako to da postavim za nalazenje konstantni. Naime, ja odredim resenja homogene diferencijalne tako sto stavim smenu y'=z(x) i onda se dobije jednacina koja razdvaja promenljive i posle kad zamenim konturne uslove, ovo sa |y(0)|<oo ne znam sta da radim. Posle je Green sablon tu.

Radi sa , gde je neka za sada neodređena konačna konstanta ili jednostavno svuda piši u postupku, pa kad rešiš jednačinu u zavisnosti od onda se javi ako ti i dalje ne bude jasno.

Koliko vidim, jednačina se svodi na . Dakle,

, .

Dalje je

,

pa je

.

Dakle,

.

Dakle, treba da integral bude konačan. To je ono što treba da dobiješ, a ti radi metodama funkcije Grina.

Ja dobijem homogenu y(x)=c1lnx+c2, 0<=x<t<=1
i y(x)=c3lnx+c4, 0<=t<=x<=1
iz uslova y(1)+y'(1)=0 => c3=-c4
a ne znam kako sad da suzim izbor za c1 i c2 pomocu ovo y(0)
posle toga, konstante posle napisemo kao funkcije koje zavise od t, preko neprekidnosti nadjemo veze, odradimo izvode bla bla i resimo sistem i dobijemo te funkcije od t.
i opste resenje se dobije integral od 0 do 1 (G(x,t)f(t)dt)... tako da bi mi znacilo kad bi uradio to sa y(0) samo dok nadjem vezu izmedju tih konstanti ili tkao nesto.

Da li bi mogao da napišeš celu i tačnu postavku zadatka?

Napisao sam u prvom postu.

Odrediti Green-ovu funkciju konturnog problema
xy"+y'=f(x), |y(0)|<oo, y(1)+y'(1)=0, a zatim odrediti partikularno rešenje date diferencijalne jednačine