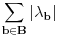[ berazorica @ 02.05.2012. 20:17 ] @
Nemam baš jasnu sliku o odnosu između nekih prostora. Može li mi neko dati primere: metričkog prostora koji nije normiran, normiranog koji nije pred-Hilbertov, pred-Hilbertovog koji nije Hilbertov? Gde su tu smešteni Banahovi prostori, tj. kakav je odnos između Banahovih i pred-Hilbertovih prostora? Ako je ova slika u redu, može li mi neko dati primer Banahovog prostora koji nije pred-Hilbertov i obrnuto?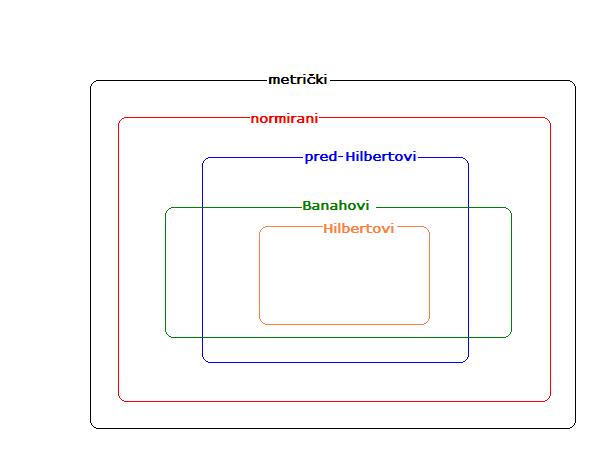 U stvari, šta znači normiran prostor? Ako imamo preslikavanje sa definisanim osobinama, onda za njega možemo reći da je norma, a odgovarajući prostor normiran, ali znamo li koji prostor može da se normira? Isto pitanje za sklalarni proizvod. Ima li onda uopšte smisla ova moja slika? Kako vi, pametni momci, poimate ove stvari? Zadovoljite se samo time da stalno imate u vidu definicije ili imate neku slikovitu predstavu? (nemojte mi samo reći da je poodavno trebalo da uđem u fazu apstraktnog mišljenja Zahvaljujem onom ko mi rasvetli ove nedoumice, a da mu ne bude preterano smešno što ih imam. [Ovu poruku je menjao berazorica dana 02.05.2012. u 22:37 GMT+1] [Ovu poruku je menjao berazorica dana 02.05.2012. u 22:44 GMT+1] |