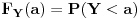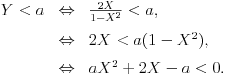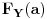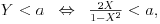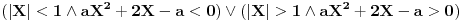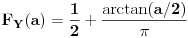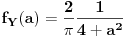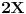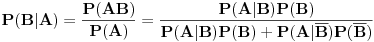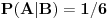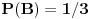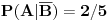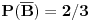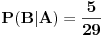1. Tri uzastopne šestice se ne mogu pojaviti pre tri uzastopne jedinice, a nešto mora da padne pre. Pošto su jedinice i šestice ravnopravne, odgovor je 1/2. To je ceo zadatak.

2. Imaš tri mogućnosti. Prebačene kuglice su obe bele, obe crne ili jedna bela, a jedna crna. Odredi verovatnoću svakog od tih događaja. Zatim odredi uslovnu verovatnoću uspeha po svakom od ta događaja, a onda iskoristi formulu potpune verovatnoće.

5. Nije ti dobro. Ovo je takođe zadatak iz potpune verovatnoće.

a sta sa kuglicama iz 1. kutije. tako sam i ja mislio kao i ti. samo sam imao 5 mogucnosti. 3 mogucnosti, kao sto si rekao za kuglice iz 2. kutije, obe bele, obe crne i jedna crna jedna bela. ali sam imao i mogucnosti da se iz 1. kutije izvuce bela ili crna. kako da to uzmem u obzir? ja sam krenuo tako. ali sam se zbunio.

a na koji nacin ide 5. zadatak. samo baci ideju? ehehe

Zbirka zadataka iz verovatnoce
http://www51.zippyshare.com/v/86509320/file.html

Nemam pojma o čemu pišeš.

Što se zadatka sa damama tiče, zbog simetrija možeš pretpostaviti da se prva dama koja se postavlja na tablu nalazi u donjoj levoj četvrtini table. Svako od polja ima verovatnoću 1/16. U svakom od slučajeva prebroj polja koja ta dama napada, tj. gde sme da se postavi druga dama na preostala 63 polja.

ajoj izvini. nisam dobro procitao zadatak. moja greska.
a ovaj zadatak sa damama. tako sam nekako i mislio. samo sam miislio prebrojati polja koja napada jedna dama i koja napada druga. to su povoljni ishodi.
to sve podeliti sa 64. brojem polja. moze tako?

Postavicu ovdje zadatak da ne pravim novu temu. Elem, slucajna promjenljiva X data je gustinom f(x) = 1/(PI*(1+x^2)). Treba naci gustin slucajne promjenljive Y = 2X/(1-X^2).

E sad nasao sam da je raspodjela od X
F(x) = arctg(x)/PI + 0.5.
Ne uspjevam da nadjem raspodjelu od Y, kao ni gustinu!

ako nisam negdje pogrjesio ispada da je gustina od Y ista kao od X. Ima li to logike?

Napiši svoj postupak, pa da vidimo.

prvo rjesim 2X/(1-X^2)=Y

i dobijem K1(y) = (-1+sqrt(1+Y^2))/Y i K2(y) = (-1-sqrt(1+Y^2))/Y

onda su izvodi K1'(y) = (sqrt(1+Y^2)-1)/(y^2*sqrt(1+Y^2)) i K2'(y) = (sqrt(1+Y^2)+1)/(y^2*sqrt(1+Y^2))

Ovo uvrstim u: g(y) = f(K1(y))*|K1'(y)| + f(K2(y))*|K2'(y)|

i dobije se g(y) = 1/PI*(y^2+1)

Moze li ovo ovako?

.



Sad lepo reši ovu nejednačinu u zavisnosti od (vodi računa o znaku), pa odredi verovatnoću da zadovolji te nejednakosti i to ti je . Onda lepo izračunaš izvod i dobiješ gustinu.

Kad rjesim ovako kako si mi rekao dobije se da je integral gustine od minus beskonacno do plus beskonacno jednak 0. A to je nemoguce.

Onda sam razdvojio slucajeve kad je x<-1, -1<x<1, 1<x
pa sam posle pet puta duzeg racuna opet dobio isti rezultat kao dva posta iznad, tj da je gustina slucajne promjenljive Y ista kao i od X. I iznosi 1/(PI*(y^2+1).
Pretpostavljam da je to tako zbog raspodjele (Kosijeva), al nisam siguran...

Ovo je za ekvivalentno sa



Kad se sve lepo izračuna, dobije se da je

,

odnosno

.

Dakle, promenljiva ima istu raspodelu kao i .

I ja imam slican problem, i treba mi pomoc. Zadatak glasi: U prvoj posudi imamo 2 bele i 1 crnu kuglicu, a u drugoj imamo 1 belu i 5 crnih kuglica. Iz prve posude smo izvadili jednu kuglicu i prebacili je u drugu posudu, a zatim smo i iz druge posude izvadili jednu kuglicu. Nakon sto smo utvrdili da je izvadjena kuglica bela, odrediti verovatnocu da je kuglica izvadjena iz prve posude i prebacena u drugu crna.

Resenje ovog zadatka je 0,2 ali ja nikako nemogu da dodjem do njega.

Hvala unapred!

je događaj da je izvađena kuglica bela, a da je iz prve posude u drugu prebačena crna. Nas zanima koliko je

.

Očigledno je

,
,
,
.

Stoga je .

pa to je slucaj sredingerove macke

http://sr.wikipedia.org/wiki/��redingerova_mačka

macka je istovremeno i ziva i mrtva, dok ne otvrorimo kutiju i vidimo da li je ziva ili mrtva.

u ovom slucaju, kuglica u kutiji je istovremeno i crna i bela, dok ne otvorimo kutiju i vidimo da li je crna ili bela.

:P

A je događaj da je iz druge posude izvađena kuglica bela.

Mogao se realizovati samo kroz 2 hipoteze:

- H1 iz prve kuglice je prebačena crna, a da je iz druge posude izvučena bele. P(H1) = (1/3)*(1/7) = 1/21
- H2 iz prve kuglice je prebačena bela, a da je iz druge posude izvučena bela. P(H2) = (2/3)*(2/7) = 4/21.

Nama treba uslovna verovatnoća hipoteze H1 ako se već desio događaj A, i ona je po Bajesovoj formuli jednaka:
(1/21) / ( (1/21) + (4/21) ) = 1/5 = 0.2

Nedeljkovo je isto rešenje, samo je kod A|B umesto 1/7 stavio 1/6, a kod A|negirano B, umesto 2/7 stavio 2/5.

_{[Ovu poruku je menjao miki069 dana 26.04.2013. u 14:13 GMT+1]}