[ M3RiM @ 13.05.2012. 22:53 ] @
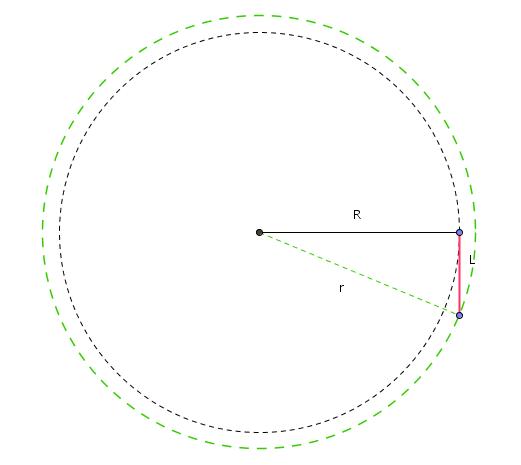
| Zadatak: Treba odrediti putanju prikolice ako je poznato da se vozilo krece po kruznici poluprecnika R, a duzina poluge kojom je prikolica vezana za vozilo je L. Uzeti za slucaj da su i vozilo i prikolica samo tačke koje se krecu po svojim kruznicama te zanemariti sve ostale faktore. Brzina je v=const ... Pretpostavljam da je ovdje potrebno upotrijebiti diferencijalne jednacine a one mi bas i nisu jaca strana.... pa bih vas zamolio za pomoc oko rjesavanja ovog zadatka... hvala [Ovu poruku je menjao M3RiM dana 14.05.2012. u 06:49 GMT+1] |