[ cikin @ 16.05.2012. 23:36 ] @
http://www.wolframalpha.com/in...8y%5E2%29%2F4%29%5E1%2F2%29%27 e sad sto me buni je kako dobiju ovo kad rade izvod pod korenom...znam da ide 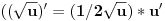 .... .... |
|
[ cikin @ 16.05.2012. 23:36 ] @
[ miki069 @ 16.05.2012. 23:55 ] @
Pošto se radi izvod po Y u pitanju je izvod proizvoda.
Posle je samo sređen rezultat. [ cikin @ 17.05.2012. 12:51 ] @
ako moze neko, kome nije tesko da napise ceo postupak.....
[ Nedeljko @ 17.05.2012. 13:31 ] @
Napiši šta ti misliš kako bi trebalo.
[ igorpet @ 17.05.2012. 16:13 ] @
Citat: cikin: ako moze neko, kome nije tesko da napise ceo postupak..... Malo nezgrapno, ali kada radi masina to tako bude :) 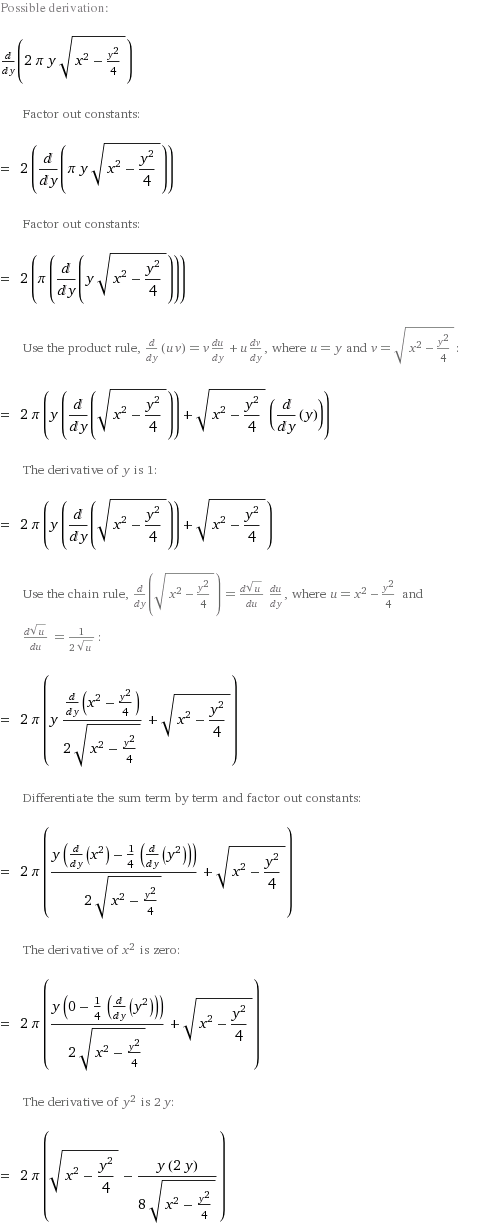 [ cikin @ 02.06.2012. 14:53 ] @
[ Nedeljko @ 02.06.2012. 16:13 ] @
Napiši ceo zadatak. Zavisi po čemu se vrši diferenciranje zapremine. Ako ti je račun dovde tačan, onda se očigledno diferenciranje vrši po H. U opštem slučaju R i H mogu da budu funkcije nekog parametra po kome se vrši diferenciranje, tako da treba videti kako zapravo glasi zadatak.
[ zzzz @ 02.06.2012. 22:41 ] @
Citat: Nedeljko: Napiši ceo zadatak. .................. U opštem slučaju R i H mogu da budu funkcije nekog parametra po kome se vrši diferenciranje, tako da treba videti kako zapravo glasi zadatak. Ne valja ti ovakva "pomoć".oj Neđeljko! Ovdje V ovisi o jednoj ili dvije varijable (R,H).Ako su obe onda radi parcijalno diferenciranje,a ako je jedna onda kao i obično,..samo po njoj tuci. A sad to tvoje: "funkcije nekog parametra",okači privremeno mačku o rep. [ cikin @ 04.06.2012. 14:01 ] @
ma zadatak : visina prave kupe minimalne zapremine opisane oko sfere poluprecnika R...to znam kad zapreminu izrazavam preko H i R ali kako da izrazim: najveca zapremina prave kupe izvdnice s iznosi?
[Ovu poruku je menjao cikin dana 04.06.2012. u 15:18 GMT+1] [ zzzz @ 04.06.2012. 21:46 ] @
Za zadato R visina kupe H i radijus baze r su međuzavisni.Tu međuzavisnost možeš naći iz sličnosti trokutova.H/R=s/r,
a s^2=H^2+r^2.Sad eliminiši ili H ili r u jednačini za zapreminu. Imaćeš funkciju jedne varijable,nađeš izvod i izjednačiš sa nulom. Sad ovo drugo:Zadano s,nađi Vmax?Jel to problem? Po Rolovom teoremu mora postojati maksimum jer za H=s i r=s zapremine su nula.Između dvije nule mora biti maksimum. Ovdje napiši formulu za zapreminu V=f(r,H),zatim eliminiši ili r ili h. s^2=H^2+r^2 (s je zadana konstanta) Probaj obe varijante V=f(r) i V=f(H) da uočiš šta je jednostavnije. [ Nedeljko @ 05.06.2012. 07:52 ] @
zzzz
H i R mogu biti funkcije istog parametra zavisno od toga kako glasi zadatak. Parcijalno diferenciranje se u srednjoj školi ne radi. Tako da tvoje parcijalno diferenciranje okači mačku o rep. Ovo drugo uputstvo ti je dobro (eliminacija jedne promenljive), ali ti proporcija iz sličnosti trouglova ne valja. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|