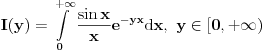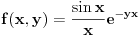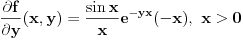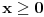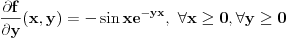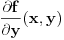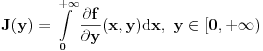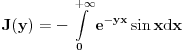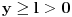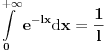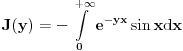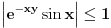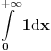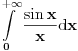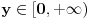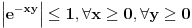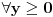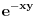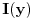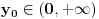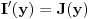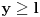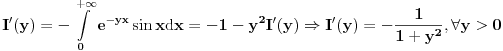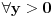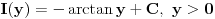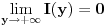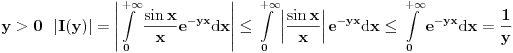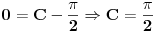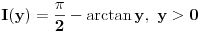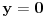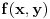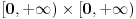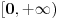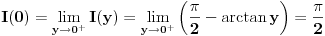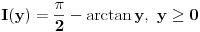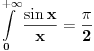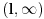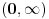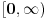|
|
[ Sonec @ 19.05.2012. 14:31 ] @
|
| Interesuje me da li sam dobro resio sledeci zadatak:
Izracunati 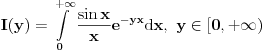 . .
Resenje. Neka je 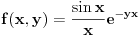 . Dodefinisimo funkciju . Dodefinisimo funkciju  tako da ona bude neprekidna (na zadatim intervalima): tako da ona bude neprekidna (na zadatim intervalima):

Dalje, 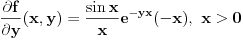 , ali kako vazi i za , ali kako vazi i za  , to mozemo reci da vazi za , to mozemo reci da vazi za 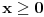 . .
Dakle, 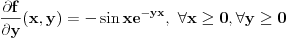 , tj. funkcija , tj. funkcija 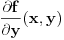 je neprekidna. je neprekidna.
Dalje, treba pokazati da 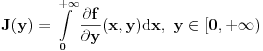 , odnosno , odnosno 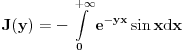 ravnomerno konvergira po ravnomerno konvergira po  . .
Za 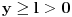 vazi vazi  (sto (ogranicenje) ne zavisi od (sto (ogranicenje) ne zavisi od  ), a kako ), a kako 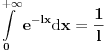 (odnosno konvergira), to prema Vajerstrasovoj teoremi i (odnosno konvergira), to prema Vajerstrasovoj teoremi i 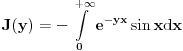 ravnomerno konvergira za ravnomerno konvergira za 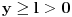 . (ako se ne bismo malo odmakli od nule, imali bismo problem ako hocemo da pokazemo preko Vajerstrasa, jer bi jedino mogli da kazemo da . (ako se ne bismo malo odmakli od nule, imali bismo problem ako hocemo da pokazemo preko Vajerstrasa, jer bi jedino mogli da kazemo da 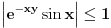 , a integral , a integral 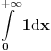 divergira, pa ne mozemo preko Vajerstrasa) divergira, pa ne mozemo preko Vajerstrasa)
Dalje, moze se pokazati da 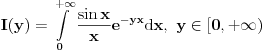 ravnomerno konvergira po ravnomerno konvergira po  . Naime, . Naime, 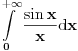 konvergira (u 0 je limes 1, u beskonacnosti Dirihle), a kako ne zavisi od parametra konvergira (u 0 je limes 1, u beskonacnosti Dirihle), a kako ne zavisi od parametra  on i ravnomerno konvergira po on i ravnomerno konvergira po 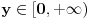 . Dalje, funkcija . Dalje, funkcija 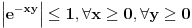 i i 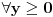 funkcija funkcija 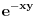 je opadajuca (po je opadajuca (po 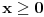 ). Pa su ispunjeni uslovi Abelove teoreme i mozemo reci da ). Pa su ispunjeni uslovi Abelove teoreme i mozemo reci da 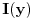 ravnomerno konvergira po ravnomerno konvergira po  . (primetimo da za uslov teoreme (koja sledi) nam nije potrebno da . (primetimo da za uslov teoreme (koja sledi) nam nije potrebno da 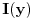 ravnomerno konvergira po ravnomerno konvergira po  , vec je dovoljno da , vec je dovoljno da 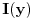 konvergira za bar jedno konvergira za bar jedno 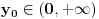 (sto i vazi, cak konvergira i u svim kao sto je upravo pokazano), ali da ce nam kasnije zatrebati ova osobina funkcije (sto i vazi, cak konvergira i u svim kao sto je upravo pokazano), ali da ce nam kasnije zatrebati ova osobina funkcije 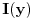 ) )
Prema jednoj od teorema (ciji su uslovi provereni u prethodnom delu) vazi 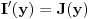 za za 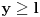 . Dakle, za . Dakle, za 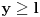 vazi vazi
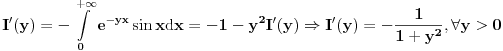 , integral se resava posle dve parcijalne (mozemo reci za , integral se resava posle dve parcijalne (mozemo reci za 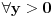 jer je jer je  bilo proizvoljno (naravno, takvo da vazi bilo proizvoljno (naravno, takvo da vazi  )) ))
Odnosno, dobijamo da je 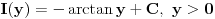 . .
 mozemo naci iz mozemo naci iz 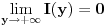 , jer je za , jer je za 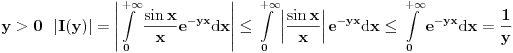 . Dakle, dobijamo da vazi . Dakle, dobijamo da vazi 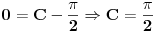 , odnosno , odnosno 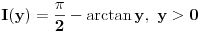 . .
E sad, treba izracunati integral i za 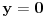 . .
To bi moglo ovako, 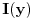 ravnomerno konvergira po ravnomerno konvergira po 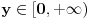 , a , a 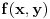 je neprekidna na je neprekidna na 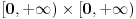 , tako da prema jednoj od teorema vazi i da je , tako da prema jednoj od teorema vazi i da je 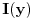 neprekidna na neprekidna na 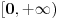 , pa vazi , pa vazi 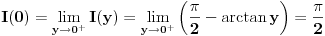 . Pa vazi (kada se sve sklopi) da je . Pa vazi (kada se sve sklopi) da je 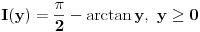 . .
Odavde se moze videti i da je Dirihleov integral 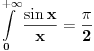 . . |
[ Nedeljko @ 19.05.2012. 21:08 ] @
Sjajno. Tako se radi analiza 2. Nemoj da nisi dobio 10, uši ću da ti iščupam!
[ Nedeljko @ 19.05.2012. 22:55 ] @
Imam jednu primedbu. Iz ravnomerne konvergencije na 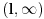 za svako  ne sledi ravnomerna, već lokalno ravnomerna konvergencija na 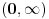 , a uz konvergenciju u nuli i lokalno ravnomerna konvergencija na 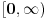 . No, za razmatranje lokalnih osobina kao što su neprekidnost i diferencijabilnost, to je dovoljno. [ Sonec @ 19.05.2012. 23:14 ] @
Da, da, vidim sta hoces da kazes. Meni je isto taj deo bio malo sumnjiv, osecao sam da nesto fali, ali nisam mogao da vidim sta. Moram takodje priznati da se do sada nisam cesto susretao sa terminom lokalne ravnomerne konvergencije (i slicno), mislim prvenstveno na vezbe, za predavanje to ne mogu reci, jer obicno se sve svodi na ispitivanje neprekidnosti i diferencijabilnosti, tako da se cak, usudio bih se reci, ti pojmovi uzimaju kao "ekvivalentni". Hvala na tome i na proveri resenja.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|