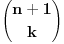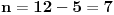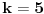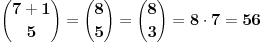[ MajorFatal @ 24.05.2012. 12:24 ] @
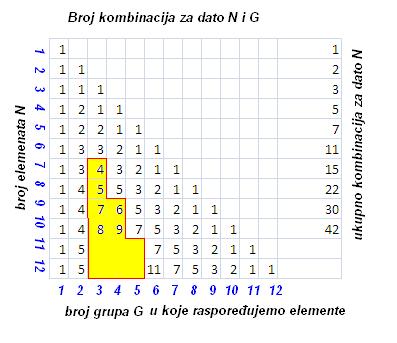
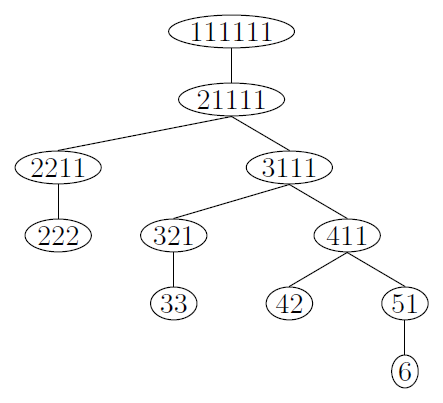
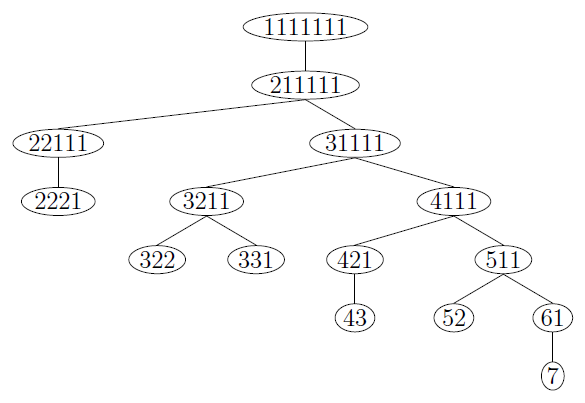
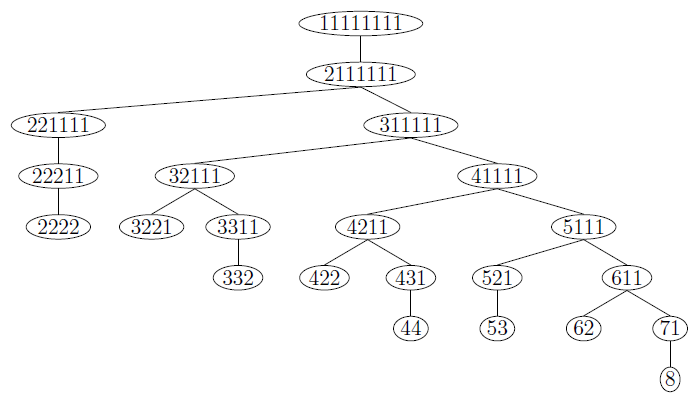
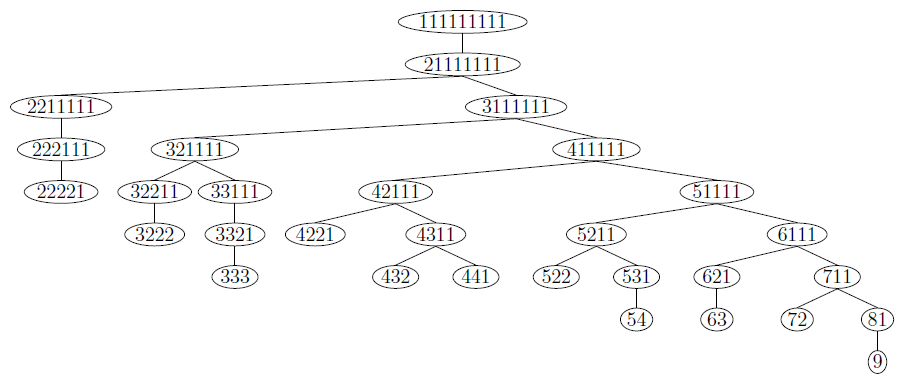
| 20 elemenata nekog skupa treba podeliti na grupe. Elementi su medjusobno identicni. Na koliko razlicitih nacina to moze da se uradi? Kad pitam na koliko razlicitih nacina mislim na: 1.) nacin: svih 20. u 1. grupi, 2.) nacin: 19. u 1. grupi i 1. u 2. grupi, .. .. x.) 20. elemenata u 20. grupa. Ovo mu dodje valjda neka kombinatorika ali ja ne mogu da prepoznam ni permutacije, ni varijacije, ni kombinacije, ti zadaci su, bar ono sto sam ja ucio uvek sa razlicitim elementima a ako ima istih elemenata deli se sa faktorijelom broja elemenata koji se ponavlja, a ovde se svi elementi ponavljaju? Ako raspisem kombinacije za neki manji broj elemenata ne mogu da uocim bilo kakvo pravilo a za veci broj elemenata ne mogu da ispisem sve kombinacije. Da li moze neko da pomogne? |