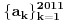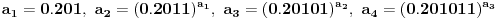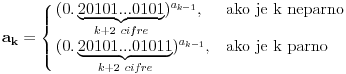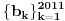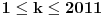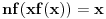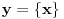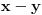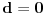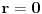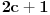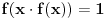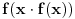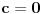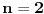[ Sonec @ 02.06.2012. 15:38 ] @
|
[ darkosos @ 04.06.2012. 08:59 ] @
Jedna ideja za ovaj drugi:
prvo pokazati da je f(x) neprekidna; dalje, primetimo da je f(c)=1 za cele brojeve c, i to je ujedno i max ove funkcije, kao i to da su nule funkcije svi x za koje je {x}=0.5; ideja je dakle da se nadje kada x(f(x) ima takve vrednosti, odnosno kada je xf(x) ceo broj, a kada je {xf(x)}=0.5, jer onda bismo imali da izmedju svaka dva cela broja postoji nekoliko max i min ove funkcije; posto je neprekidna, onda uzima sve vrednosti izmedju 0 i 1, pa dakle sigurno sece x/n za neko n. Onda jos sve to lepo sabrati i videti kada se prelazi 2012 :) Ako nadjem vremena, probacu da dovrsim, ako ne moze neko da nastavi... EDIT: malo sam se nalupao, obrisao sam to, ideja ostaje... [Ovu poruku je menjao darkosos dana 04.06.2012. u 23:04 GMT+1] [ darkosos @ 04.06.2012. 23:34 ] @
Mozda cu da lupam, ali sta cu, ne da mi mira :)
Elem, nastavljajuci ideju, prvo sam pokusao da razmotrim kada je xf(x) ceo broj. Posto je inace f(x)>=0 za sve x, razmatracu samo pozitivne brojeve. Neka je c prirodan broj; pitanje je koliko ima brojeva oblika x=c+r, gde je r iz intervala (0,1), za koje je xf(x) ceo broj; 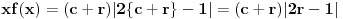 . Naravno, ako je ovo ceo broj, onda je to i . Naravno, ako je ovo ceo broj, onda je to i 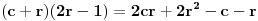 i opet mozemo da zanemarimo -c, pa trazimo da je i opet mozemo da zanemarimo -c, pa trazimo da je 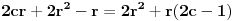 ceo broj. ceo broj.Ne znajuci sta drugo, probao sam ovako: neka je d ceo broj, 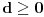 ; posmatramo jednacinu ; posmatramo jednacinu 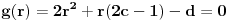 . Trazimo da ova jednacina (po r) ima bar jedno resenje u (0,1). Diskriminanta je . Trazimo da ova jednacina (po r) ima bar jedno resenje u (0,1). Diskriminanta je 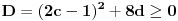 , pa uvek postoje resenja. x-koordinata temena je , pa uvek postoje resenja. x-koordinata temena je 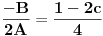 sto ce upasti u (0,1) samo ako je c=0, sto sada ne razmatram. Sledi da ne mogu oba resenja biti u (0,1). Dalje, posto je sto ce upasti u (0,1) samo ako je c=0, sto sada ne razmatram. Sledi da ne mogu oba resenja biti u (0,1). Dalje, posto je 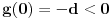 a a 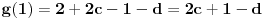 , jedina mogucnost je da je g(1)>0 tj , jedina mogucnost je da je g(1)>0 tj 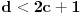 sto daje sto daje 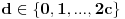 Ako nisam nesto pogresio, ovo je zapravo broj nula funkcije f(xf(x)) u intervalu (c,c+1), tj. ima ih 2c+1. [ Nedeljko @ 05.06.2012. 07:26 ] @
[ darkosos @ 05.06.2012. 08:28 ] @
Da, setio sam se da sam zas*ao na kraju, ali je komp vec bio ugasen :) Elem, hvala na ispravci, probacu da dovrsim (idejni okvir je postavljen, treba jos malo tehnikalije)...
[ darkosos @ 05.06.2012. 12:12 ] @
Drugi korak: odrediti broj resenja jednacine
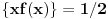 u intervalu u intervalu 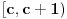 Uz zadrzavanje prethodnih oznaka, iz 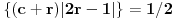 sledi da je sledi da je 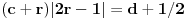 za neki ceo broj za neki ceo broj 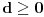 (leva strana je pozitivna pa mora biti i desna). Posto mi je upalilo prosli put, nastavicu odredjivanje broja resenja na isti nacin. Na zalost, ovde se ne moze izbeci apsolutna vrednost... Posebno, za r=1/2, bice 0=d+1/2 sto nema resenja u Z. Takodje, za r=0, bice {c}=1/2 sto je opet nemoguce (uostalom to upada u prethodno razmatranje). (leva strana je pozitivna pa mora biti i desna). Posto mi je upalilo prosli put, nastavicu odredjivanje broja resenja na isti nacin. Na zalost, ovde se ne moze izbeci apsolutna vrednost... Posebno, za r=1/2, bice 0=d+1/2 sto nema resenja u Z. Takodje, za r=0, bice {c}=1/2 sto je opet nemoguce (uostalom to upada u prethodno razmatranje).Neka je prvo 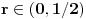 . Gornja jednacina se transformise u (preskocicu detalje) . Gornja jednacina se transformise u (preskocicu detalje) 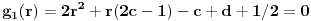 . Posto je . Posto je 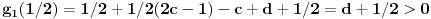 , mora biti , mora biti 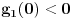 tj. tj. 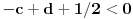 odakle dobijamo odakle dobijamo 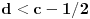 odnosno odnosno 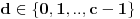 , pa ovde imamo c resenja za r. , pa ovde imamo c resenja za r.Neka je sada 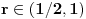 , jednacina je , jednacina je 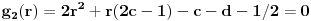 , , 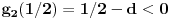 pa mora biti pa mora biti 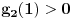 tj. tj. 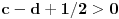 , odnosno , odnosno 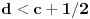 , sto nam daje , sto nam daje 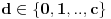 , pa sada imamo c+1 resenja za r. , pa sada imamo c+1 resenja za r.Gle cuda, ispada da i nula funkcije ima 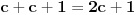 u intervalu u intervalu 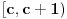 . E sad, ko stigne nek' pregleda ova moja pisanija, mislim da je vreme da mu zadam poslednji udarac :) u sledecem broju. . E sad, ko stigne nek' pregleda ova moja pisanija, mislim da je vreme da mu zadam poslednji udarac :) u sledecem broju.(sada sam video da ovo da je -d+1/2<0 nije tacno za d=0, ali izgleda da za d=0 opet postoji jedno resenje u (1/2,1)) [ darkosos @ 05.06.2012. 22:29 ] @
Nisam bas sve detalje razradio kako bih zeleo, ali evo:
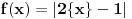 je neprekidna jer je je neprekidna jer je 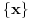 inace neprekidna na svim intervalima (c,c+1) za cele brojeve c, a posto je inace neprekidna na svim intervalima (c,c+1) za cele brojeve c, a posto je 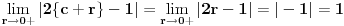 kao i kao i 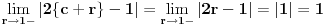 , ova funkcija lepo spaja levi i desni kraj na takvim intervalima. Odavde naravno sledi i da je , ova funkcija lepo spaja levi i desni kraj na takvim intervalima. Odavde naravno sledi i da je 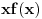 neprekidna, pa je koancno takva i neprekidna, pa je koancno takva i 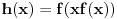 kao kompozicija dve neprekidne. kao kompozicija dve neprekidne.Pa, ako su prethodna razmatranja tacna, na intervalima 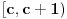 funkcija h(x) dostize 2c+1 puta vrednost 0 i isto toliko puta vrednost 1. Ima jedna sitnica, trebalo bi pokazati da izmedju svake dve nule ima jedan kec, da bi funkcija zaista isla cik-cak, ali nesto me to mrzucka sada... Takodje, treba razmrsiti sta se dogadja u intervalu (0,1), posto tu ima i jedan lokalni minimum koji nije 0, ali i to cu preskociti... funkcija h(x) dostize 2c+1 puta vrednost 0 i isto toliko puta vrednost 1. Ima jedna sitnica, trebalo bi pokazati da izmedju svake dve nule ima jedan kec, da bi funkcija zaista isla cik-cak, ali nesto me to mrzucka sada... Takodje, treba razmrsiti sta se dogadja u intervalu (0,1), posto tu ima i jedan lokalni minimum koji nije 0, ali i to cu preskociti...Posto 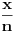 tacno pogadja tacku tacno pogadja tacku 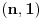 , koja pripada i grafiku funkcije h(x), da probamo da prebrojimo broj preseka za neko dato n, grafika funkcije x/n i h(x). U intervalu [c-1,c), za , koja pripada i grafiku funkcije h(x), da probamo da prebrojimo broj preseka za neko dato n, grafika funkcije x/n i h(x). U intervalu [c-1,c), za 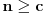 , x/n sece , x/n sece 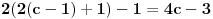 puta (uzeo sam c-1 jer se onda kraj poslednjeg intervala poklapa sa n). Racunajuci i poslednju tacku, (n,1), ukupan broj preseka je puta (uzeo sam c-1 jer se onda kraj poslednjeg intervala poklapa sa n). Racunajuci i poslednju tacku, (n,1), ukupan broj preseka je 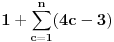 a to je dalje jednako a to je dalje jednako 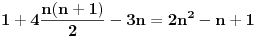 . Dakle, posle svega ovoga, treba jos resiti jednacinu . Dakle, posle svega ovoga, treba jos resiti jednacinu 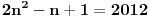 , tj naci najamanje n za koje se dostize vrednost jednaka ili veca od 2012. Pozitivno resenje ove jednacine je priblizno 31.96, a kako je tu funkcija , tj naci najamanje n za koje se dostize vrednost jednaka ili veca od 2012. Pozitivno resenje ove jednacine je priblizno 31.96, a kako je tu funkcija 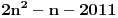 rastuca, moj konacan odgovor je 32, gde bi imali 2017 preseka. rastuca, moj konacan odgovor je 32, gde bi imali 2017 preseka.Ako sam i negde oman'o, vec ce neko ispraviti, ali mislim da sam na pravom putu. [ darkosos @ 07.06.2012. 08:48 ] @
Hmmm, da jeste, evo gledam grafik... Izgleda da sam dobro izracunao broj jedinica i nula, ali preseka sa tip cik-cakom ima 2(2c+1) bez onog -1, koje sam dodao kao zao sto gadja vrh, ali to je naravno samo na kraju, gde se prakticno opet dodaje bas zog tog vrha :) Imajuci to na umu, onda bi bilo 4c-2 preseka po intervalu, tj. ukupan broj preseka bi bio
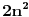 . I na kraju, . I na kraju, 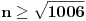 , dakle opet 32. , dakle opet 32.[ Sonec @ 07.06.2012. 11:49 ] @
[ darkosos @ 07.06.2012. 12:27 ] @
Pa, da, kada sam video grafik, shvatio sam da, kada zakljucis da ide cik-cak izmedju 0 i 1, treba prebrojati samo npr. 0 i onda zakljuciti da je broj preseka duplo veci od broja nula. U ovom slucaju to je 2(2c+1), s tim sto je lakse da se ide na c-1, tj 2(2(c-1)+1) = 4c-2. I naravno, onda samo sabrati od 1 do n. Jel' ovo zadatak sa nekog takmicenja? Oni vole da koriste tekuce godine u zadacima... Prob'o bih ja i prvi, ali i za ovaj sam se iscimao, s' obzirom na moje obaveze :)
[ Nedeljko @ 07.06.2012. 16:05 ] @
Pridružujem se čestitkama i molim Bojana Bašića da ne kvari drugima zabavu oko prvog zadatka. Zaista je lakši. Neka neko proba da sortira prvih nekoliko članova niza. To je dobar osnov za početak.
[ Sonec @ 07.06.2012. 19:33 ] @
Citat: darkosos: Jel' ovo zadatak sa nekog takmicenja? Oni vole da koriste tekuce godine u zadacima... Izvor zadataka cu reci posto se resi i prvi zadatak. Al da, moze se reci da je zadatak sa takmicenja (ili pak predlog za takmicenje, nisam siguran). [ darkosos @ 08.06.2012. 07:51 ] @
Ne interesuje me bas izvor, samo to da li je sa takmicenja, na sta sam dobio odgovor :). I to zato sto nikad nisam isao na ta takmicenja, pa mi je jos veci izazov da resim takav zadatak... A tvrdoglav jesam :) I izgleda kao da svi sem mene znaju kako se resavaju ovi zadaci, pa vam je ovo dosao kao prenos nekog meca :) Anyway, ne znam ko bi se jos latio tog prvog zadatka, meni treba kriticna masa vremena da bih dosao na ideju, a ostali znaju kako se radi ili ih ne zanima ič.
[ Nedeljko @ 08.06.2012. 10:18 ] @
Nemoj misliti da svi ostali znaju, ali dao sam ti osnovu za početak da vidiš kako izgleda sortiran niz od prvih nekoliko članova u odnosu na nesortiran.
[ darkosos @ 09.06.2012. 23:00 ] @
Ako tema ode sa prve strane, onda cao :) U svakom slucaju, posto vec niko nece, a nekako se osecam prozvanim :) onda 'vako:
Trebalo bi prvo uspostaviti odnose izmedju tih osnova, neka je to npr. niz 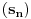 , gde je , gde je 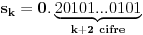 ako je k neparno i ako je k neparno i 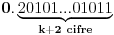 ako je k parno. Rekao bih da se lako vidi da je podniz sa neparnim indeksima rastuci niz, jer je odnos ako je k parno. Rekao bih da se lako vidi da je podniz sa neparnim indeksima rastuci niz, jer je odnos 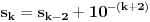 za neparne za neparne 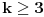 . Takodje, podniz sa parnim indeksima je opadajuci, jer je . Takodje, podniz sa parnim indeksima je opadajuci, jer je 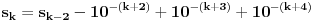 za parne za parne 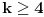 . .Primetimo i da je svaki clan niza sa neparnim indeksom manji od narednog - koji naravno ima paran indeks, jer se prakticno takav sledeci dobija samo dodavanjem jedinice na kraj niza decimala. Ova cinjenica sa prethodnim daje da je svaki clan niza sa neparnim indeksom manji od svakog clana niza sa parnim indeksom. Ne znam da li to treba da se dokazuje posebno, radi se o tome da je za svaki clan na parnom mestu 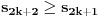 , leva strana manja od svih prethodnih na parnim mestima (jer ovaj podniz opada) a desna veca od svih prethodnih na neparnim mestima (jer ovaj podniz raste). , leva strana manja od svih prethodnih na parnim mestima (jer ovaj podniz opada) a desna veca od svih prethodnih na neparnim mestima (jer ovaj podniz raste).Uh, eto to je to o osnovama. Posto mi polako mozak istice, ostavicu nesto i za sutra :). Trebalo bi da moze da se dokusuri cinjenicom da je 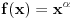 rastuca funkcija za rastuca funkcija za 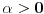 kao i da je kao i da je 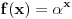 opadajuca funkcija za opadajuca funkcija za  . .[ darkosos @ 10.06.2012. 20:53 ] @
Primetimo jos i da je
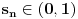 za sve prirodne n. Posto je za sve prirodne n. Posto je 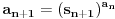 i i 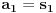 i svi clanovi niza a takodje su u i svi clanovi niza a takodje su u  . .U daljim procenama cu koristiti osobine dve familije funkcija koje sam naveo u prosloj poruci, tj. da je: 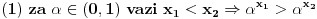 i i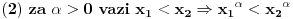 Pogledacemo prvo, sto bi rek'o Nedeljko, nekoliko prvih clanova niza, tacnije utvrdicemo odnos izmedju prvih cetiri: Koristeci nejednakost iz prethodne poruke, imamo: 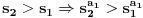 , , 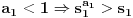 sto zapravo daje sto zapravo daje 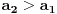 . .Dalje imamo: 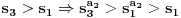 , , 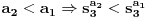 i i 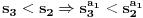 sto zapravo znaci da je sto zapravo znaci da je 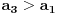 i i 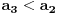 odnosno da je redosled odnosno da je redosled 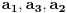 . Skraticu dalje malo, mislim da je jasna taktika: . Skraticu dalje malo, mislim da je jasna taktika: 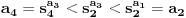 i i 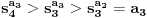 , sto daje redosled , sto daje redosled 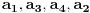 . .U ovom poslednjem sam koristio vec utvrdjenu nejednakost 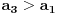 , sto nas navodi na zakljucak da nejednakosti ne mozemo izvoditi samostalno, vec indukcijom, tj. oslanjajuci se na prethodno. Izgleda da niz a prati nejednakosti niza s, pa cu pokusati da dokazem da elementi sa neparnim indeksima rastu i svi su manji od onih na pranim mestima i da ovi poslednji obrazuju opadajuci niz (opet cik-cak, slucajnost?). , sto nas navodi na zakljucak da nejednakosti ne mozemo izvoditi samostalno, vec indukcijom, tj. oslanjajuci se na prethodno. Izgleda da niz a prati nejednakosti niza s, pa cu pokusati da dokazem da elementi sa neparnim indeksima rastu i svi su manji od onih na pranim mestima i da ovi poslednji obrazuju opadajuci niz (opet cik-cak, slucajnost?).U stvari, mislim da bih samo dzabe trosio "papir" oko toga, prilicno je ocigledno da se prethodno rezonovanje moze primeniti na bilo koju cetvorku uzastopnih elemenata posmatranog niza, koji pocinje sa neparnim indeksom. Ako je to zaista tako, onda bi redosled bio  . Posto su svi elementi niza medjusobno razliciti, jedini nacin da se poklopi vrednost je da se poklopi indeks. Prvih 1005 indeksa (koja je mnozina od indeks?) uredjenog niza su zapravo dvostruke vrednosti prvih 1005 originalnog niza, pa tu nema poklapanja. Ostalih 1006 indeksa su oblika . Posto su svi elementi niza medjusobno razliciti, jedini nacin da se poklopi vrednost je da se poklopi indeks. Prvih 1005 indeksa (koja je mnozina od indeks?) uredjenog niza su zapravo dvostruke vrednosti prvih 1005 originalnog niza, pa tu nema poklapanja. Ostalih 1006 indeksa su oblika 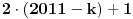 a to ce se poklopiti sa k za a to ce se poklopiti sa k za 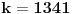 , sto se naravno dobija iz jednacine , sto se naravno dobija iz jednacine 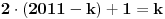 . .Postavka zadatka sugerise da ih ima vise, pa je moguce da sam negde oman'o. Ako nisam, odgovor je 1341. [ Sonec @ 10.06.2012. 21:15 ] @
Dobro je.
1. 2. [ darkosos @ 10.06.2012. 21:37 ] @
I ja da ubodem iz prve :) A ovaj lik prica kao za nekog ko ne poznaje eksponencijalne funkcije, zanimljivo, kako misli da resi ovakav zadatak?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|