.

Postoji li neki drugi nacin?

Mislim da je pisac zamislio, baš taj način, a može i drugačije. Na primer, primenom Lagranževe teoreme o srednjoj vrednosti ili tako što izvučeš pa unutra koristiš Tejlora za .

Definitivno je mislio na ono prvo, posto drugo nismo radili :) Hvala.

Kako ovaj?

Iskoristi ovo za .

A kako da znam koji broj da uzmem za n?

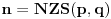
Ove izraze oblika u kojima zelis da se oslobodis korenja, mozes srediti tim izrazom koji je Nedeljko dao. Da bi napravio celim te stepene, a stepenujes ih istim brojem, to mozes uciniti sa NZS(p,q). Onda radis kao da je i naravno, u toj formuli. Mnozeci a-b sa onim povelickim izrazom dole, dobijas to sto ti treba. Konkretno, kod tebe je n=NZS(2,3)=6.

Je l' se i ovaj radi na isti nacin?




EDIT: tj. ne, ovaj ide preko onog tablicnog, sad videh.

Gde gresim? Treba da mi ispadne , ali nikako ne mogu to da dobijem.

Pa breee, tg(x+y) nije isto sto i tg(x)+tg(y).

Znaci:

I odavde dobijam , negde mi se gubi . :/

Ne znam kako si to dobio. Skrati sa sve da se rascisti, pa ako vec menjas sa , dobija se .

O cemu li ja mislim, radio sam kao da je , umesto !

Hvala Darko :)

Kada Ln-uju u zbirci, ostaje: .


Buni me ovo , odakle to? Verovatno ima veze sa ovim , ali ne znam kako.

Previse si se opustio :) Lepo logaritmuj sve to sto je pod limesom i sredi izraz.

Pokusavam, ali ne ide...

. Pretpostavljam da znas da je ln(e)=1?

_{[Ovu poruku je menjao darkosos dana 12.06.2012. u 09:00 GMT+1]}