.

Odavde se lako izračunava .

.

Odavde se znajući lako izračunava .

Naravno, dobićeš dve vrednosti za .

Hvala ti Nedeljko, stvarno ste mi vi ljudi sa EliteSecurity-a od velike pomoći Evo još jedan: Za koje vrednosti parametra ''m'' su oba korena jednačine veća od 3?
Jednačina:
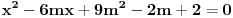
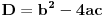
E sad, da bi oba rešenja bila veća od 3, mora valjda i determinanta D>3, gde je: . Jel se ovako radi?

Btv. za prošli sam dobio rešenja -125/8, 27/8, proverio i na volframu, tačno je.

Pogledaj http://www.elitesecurity.org/t...Re-kvadratne-jednacine-resenja

Hm.. gledam ovo....
a=1 → a>0 Parabola okrenuta na gore
D>0 → m>1 To je uslov valjda da imamo dva realna i različita rešenja..
I šta ja sad treba da uradim ovde? Da tražim uslov kada su oba pozitivna? Pa to se vidi iz uslova zadatka.

x1+x2>0
D>0
x1*x2>0 - Što važi bili oni oba pozitivna ili negativna...

To ja kontam, nije problem.. Ali kako i šta da radim kad mi je traženo da rešenja budu veća od 3??
Da stavim da x1+x2>3 ?

http://www.elitesecurity.org/t183907-0#2992486