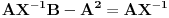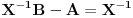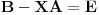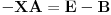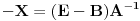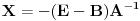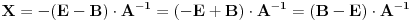[ patkan1992 @ 12.06.2012. 18:18 ] @
|
[ darkosos @ 12.06.2012. 19:30 ] @
Izgleda ok.
[ Nedeljko @ 12.06.2012. 19:52 ] @
Taj račun prolazi pod uslovom da je matrica A inverzibilna, inače ne.
[ patkan1992 @ 12.06.2012. 20:03 ] @
Ok, znaci to je to. Dalje bi proverio da li matrica A ima sebi inverznu.
A kako mogu da prebacim ovaj "-" sa druge strane? Hoce li izmeniti nesto ako ga samo prebacim, ili ima neko posebno pravilo za prebacivanje? [ darkosos @ 12.06.2012. 20:05 ] @
Samo prebaci, -X je -1*X dakle proizvod skalara i matrice.
[ patkan1992 @ 12.06.2012. 21:11 ] @
[ darkosos @ 13.06.2012. 07:40 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|